树-二叉搜索树的排序问题

Posted 2020-12-26 huting-front

遍历一棵树是指访问树的每个节点并对它们进行某种操作的过程。访问树的所有节点的方式有三种：中序、先序、后序。

中序遍历是一种以上行顺序访问BST所有节点的遍历方式，也就是从小到达的顺序访问所有节点。中序遍历的一种应用就是对树进行排序操作。

以上是中序排列的编写，使用了一个辅助私有函数，来接收一个节点和对应的回调函数作为参数，最常使用的算法是递归。通过使用以上函数，在控制台上的输出结果是从小到大的排列的数。

先序遍历是以优于后代节点的顺序访问每个节点的，先序遍历的一种应用是打印一个结构化的文档。

先序和中序遍历不同点是，先序遍历会先访问节点本身（行{1})，然后再访问它的左侧子节点，最后是右侧子节点。在控制台上最后输出的结果是从顶端往下的先左侧到底端，在从左侧底端往右侧底端向上遍历，最后遍历到右侧的最右边的节点。

后序遍历则是先访问节点的后代节点，再访问节点本身。后序遍历的一种应用是计算一个目录和它的子目录中的所有文件所占空间的大小。

我们来看它的实现：

后序遍历会先访问左侧的子节点，然后是访问右侧子节点，最后是父节点。

给树进行遍历之后，还可以尝试获取其最大值和最小值；方法和前面差不多，都是构造一个辅助函数，来达到我们要的效果。

在某些时候我们需要搜索一个特定的值，看是不是在这个树中，这时候可以创建一个搜索函数。

然后还可以创建一个移除函数，达到最基本的移除效果。

 

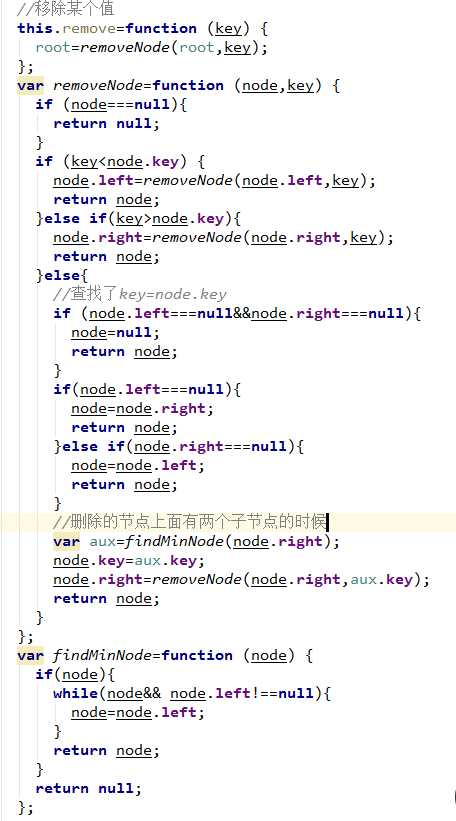
 这里我创建了一个基本二叉搜索树的遍历，搜索，删除的功能，这只是它的一些基本功能，更多的东西还需要继续学习下去，我会加油的。