线性回归
Posted qinhao2
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了线性回归相关的知识,希望对你有一定的参考价值。
创建线性回归模型
import sklearn.linear_model as lm
sklearn.linear_model.LinearRegression()->线性回归器
线性回归器.fit(输入样本, 输出标签)
线性回归器.predict(输入样本)->预测输出标签

4.94,4.37 -1.58,1.7 -4.45,1.88 -6.06,0.56 -1.22,2.23 -3.55,1.53 0.36,2.99 -3.24,0.48 1.31,2.76 2.17,3.99 2.94,3.25 -0.92,2.27 -0.91,2.0 1.24,4.75 1.56,3.52 -4.14,1.39 3.75,4.9 4.15,4.44 0.33,2.72 3.41,4.59 2.27,5.3 2.6,3.43 1.06,2.53 1.04,3.69 2.74,3.1 -0.71,2.72 -2.75,2.82 0.55,3.53 -3.45,1.77 1.09,4.61 2.47,4.24 -6.35,1.0 1.83,3.84 -0.68,2.42 -3.83,0.67 -2.03,1.07 3.13,3.19 0.92,4.21 4.02,5.24 3.89,3.94 -1.81,2.85 3.94,4.86 -2.0,1.31 0.54,3.99 0.78,2.92 2.15,4.72 2.55,3.83 -0.63,2.58 1.06,2.89 -0.36,1.99

1 import numpy as np 2 import sklearn.linear_model as lm 3 import sklearn.metrics as sm 4 import matplotlib.pyplot as mp 5 6 # x,y用来装x,y上的点 7 x, y = [], [] 8 with open(‘../ML/data/single.txt‘, ‘r‘) as f: 9 for line in f.readlines(): 10 data = [float(substr) for substr in line.split(‘,‘)] 11 x.append(data[:-1]) 12 y.append(data[-1]) 13 14 x = np.array(x) 15 y = np.array(y) 16 # print(x) 17 # 创建线性回归模型器 18 model = lm.LinearRegression() 19 # 导入数据 20 model.fit(x, y) 21 # 生成预测点 22 pred_y = model.predict(x) 23 24 # 画训练集的图像 25 mp.figure(‘Linear Regression‘, facecolor=‘lightgray‘) 26 mp.title(‘Linear Regression‘, fontsize=20) 27 mp.xlabel(‘x‘, fontsize=14) 28 mp.ylabel(‘y‘, fontsize=14) 29 mp.tick_params(labelsize=10) 30 mp.grid(linestyle=‘:‘) 31 mp.scatter(x, y, c=‘dodgerblue‘, alpha=0.55, s=60, label=‘Sample‘) 32 33 # 画线性回归的图像 34 # argsort()函数是将x中的元素从小到大排列,提取其对应的index(索引),然后输出到y。 35 sorted_indices = x.T[0].argsort() 36 mp.plot(x[sorted_indices], pred_y[sorted_indices], 37 ‘o-‘, c=‘orangered‘, label=‘Regression‘) 38 39 mp.legend() 40 mp.show()
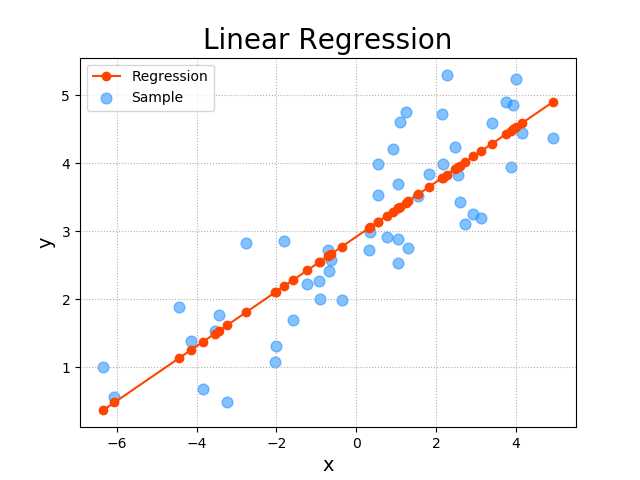
保存模型

1 import numpy as np 2 import sklearn.linear_model as lm 3 import sklearn.metrics as sm 4 import matplotlib.pyplot as mp 5 # 导入pickle 6 import pickle 7 8 x, y = [], [] 9 with open(‘../ML/data/single.txt‘, ‘r‘) as f: 10 for line in f.readlines(): 11 data = [float(substr) for substr in line.split(‘,‘)] 12 x.append(data[:-1]) 13 y.append(data[-1]) 14 15 x = np.array(x) 16 y = np.array(y) 17 model = lm.LinearRegression() 18 model.fit(x, y) 19 pred_y = model.predict(x) 20 21 # sklearn中的回归器性能评估方法 22 23 # 平均绝对值误差(mean_absolute_error) 24 print(sm.mean_absolute_error(y, pred_y)) 25 # 均方差(mean-squared-error) 26 print(sm.mean_squared_error(y, pred_y)) 27 # 中值绝对误差(Median absolute error) 28 print(sm.median_absolute_error(y, pred_y)) 29 # R2 决定系数(拟合优度) 30 print(sm.r2_score(y, pred_y)) 31 32 # 保存模型 33 with open(‘linear.pkl‘, ‘wb‘) as f: 34 pickle.dump(model, f) 35 36 mp.figure(‘Linear Regression‘, facecolor=‘lightgray‘) 37 mp.title(‘Linear Regression‘, fontsize=20) 38 mp.xlabel(‘x‘, fontsize=14) 39 mp.ylabel(‘y‘, fontsize=14) 40 mp.tick_params(labelsize=10) 41 mp.grid(linestyle=‘:‘) 42 mp.scatter(x, y, c=‘dodgerblue‘, alpha=0.55, s=60, label=‘Sample‘) 43 44 sorted_indices = x.T[0].argsort() 45 mp.plot(x[sorted_indices], pred_y[sorted_indices], 46 ‘o-‘, c=‘orangered‘, label=‘Regression‘) 47 48 mp.legend() 49 mp.show()
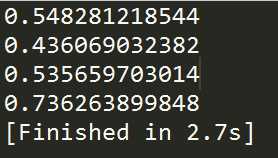
导入模型

1 import numpy as np 2 import sklearn.linear_model as lm 3 import sklearn.metrics as sm 4 import matplotlib.pyplot as mp 5 import pickle 6 7 x, y = [], [] 8 with open(‘../ML/data/single.txt‘, ‘r‘) as f: 9 for line in f.readlines(): 10 data = [float(substr) for substr in line.split(‘,‘)] 11 x.append(data[:-1]) 12 y.append(data[-1]) 13 x = np.array(x) 14 y = np.array(y) 15 16 # 导入模型 17 with open(‘linear.pkl‘, ‘rb‘) as f: 18 model = pickle.load(f) 19 pred_y = model.predict(x) 20 21 mp.figure(‘Linear Regression‘, facecolor=‘lightgray‘) 22 mp.title(‘Linear Regression‘, fontsize=20) 23 mp.xlabel(‘x‘, fontsize=14) 24 mp.ylabel(‘y‘, fontsize=14) 25 mp.tick_params(labelsize=10) 26 mp.grid(linestyle=‘:‘) 27 mp.scatter(x, y, c=‘dodgerblue‘, alpha=0.55, s=60, label=‘Sample‘) 28 29 sorted_indices = x.T[0].argsort() 30 mp.plot(x[sorted_indices], pred_y[sorted_indices], 31 ‘o-‘, c=‘orangered‘, label=‘Regression‘) 32 33 mp.legend() 34 mp.show()
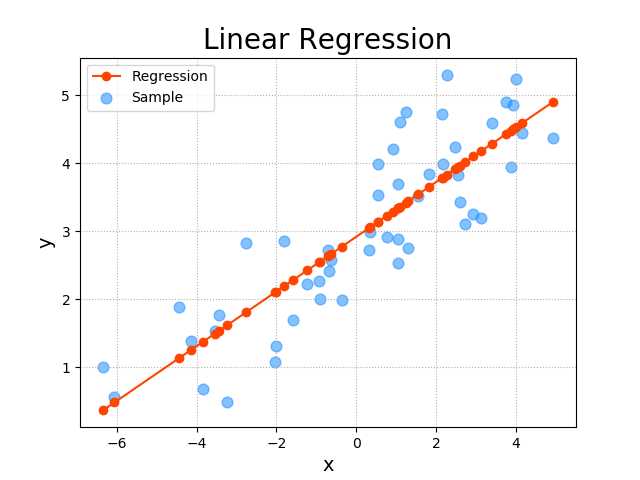
以上是关于线性回归的主要内容,如果未能解决你的问题,请参考以下文章
