bzoj1426 收集邮票

Posted 2020-12-26 miracevin

题目描述：

有n种不同的邮票，皮皮想收集所有种类的邮票。唯一的收集方法是到同学凡凡那里购买，每次只能买一张，并且买到的邮票究竟是n种邮票中的哪一种是等概率的，概率均为1/n。但是由于凡凡也很喜欢邮票，所以皮皮购买第k张邮票需要支付k元钱。
现在皮皮手中没有邮票，皮皮想知道自己得到所有种类的邮票需要花费的钱数目的期望。

N<=10000

 

题解：

k张k元不好做，先考虑每张都是1元怎么做。

设f[i]表示，已经有了i种，买到n种的期望步数，也就是期望花费。

f[i]=(i/n)*(f[i]+1) + (n-i)/n*(f[i+1]+1)  ;   ( i<n)

f[n]=0;

就是说，i/n的概率买到之前买过的邮票，(n-i)/n的概率买到新的邮票。

期望=概率*结果。理解上就是，这样的概率i/n,(n-i)/n，到达了这样的结果。就可以推出来了。

 

因为这个f数组，可以表示期望的步数，非常有用。以下讲解继续沿用。

然后，对于k张k元的情况，有两种做法：

 

（都要通过    期望=概率*事件的结果取值   来理解）

 

①（理解麻烦，过程简单）

设g[i]表示，从有了i种有邮票到买到n种邮票要花的钱数。

f[i]还和上面的一样。

所以，g[i]的转移是：

g[i]=i/n*(g[i]+f[i]+1)+(n-i)/n*(g[i+1]+f[i+1]+1)

g[n]=0;

比较难以理解。

解释：

i/n是买到自己原来买过的概率。

该种情况下，到达的结果是，还要有的g[i]花费，并且，之后期望还要买的f[i]次价格都上涨了1，总体加了f[i]，再加上这次的1花费。

为什么可以认为，这一次是第一次买，花费是1呢？？

我们在状态中，默认已经有了i张（从天上掉下来的，不花钱），所以，第一次买就是1元了。

或者，因为我们最后要求的是g[0]，

对于g[0]，第一次买花费1肯定是成立的。

所以，我们之后的所有花费，都默认第一次是1，之后计算还会加上的。

 

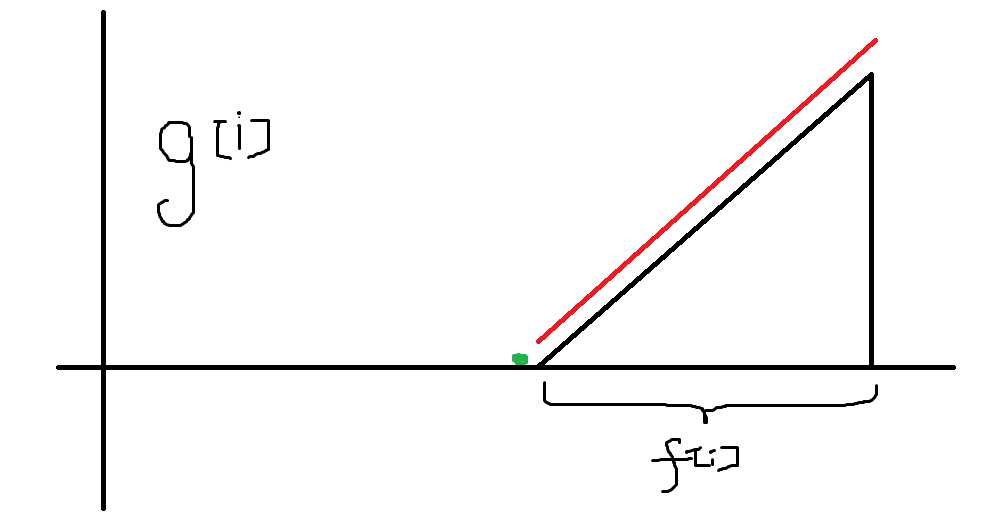
画图理解一下，g[i]的组成，黑色部分是的g[i],红色一道是增加了总体的f[i], 绿色一个点是这次操作花费的1元。

而相邻的g[i+1]->g[i]的更新时类似的。因为都加上了一个f[i+1]么，所以g[i+1]的花费1也就变成了花费2了。

 

之后拆开括号，移项，然后直接求。

 

②（理解简单，过程麻烦）

发现，假设买了k张邮票，花费就是：（k^2+k）/2     ----------------等差数列求和嘛

再确切一些，设s[i]表示，有了i种邮票，到n种邮票的步数（不是期望）

所以，f[i]=E(s[i])

所以花费的期望：E(cos)=E((s[0]^2+s[0])/2)

基于期望的线性性质，E(cos)=(   E(s[0]^2)+E(s[0])    )/2

我们已经求出了f[0]=E(s[0])

所以，要求出E(s[0]^2)   （注意，这个是平方的期望，不等于期望的平方！！）

 

设g[i]=E(s[i]^2)即从i到n步数平方的期望

因为，E((x+1）^2)=E(x^2)+2*E(x)+1

所以，g[i]=i/n*(E(  (s[i]+1)^2 ) +  (n-i)/n *(E( (s[i+1]+1)^2 )

拆开它:g[i]=i/n * ( g[i] + 2*f[i] + 1 ) + ( n - i ) * ( g[i+1] + 2* f[i+1] +1)

拆开括号，移项，然后直接求。

 

 

总结：

期望一定要小心谨慎分析，不要直觉瞎搞，设计好状态，转移。

分清楚 ： 事件，概率，结果，期望。

抓住E(x+y)=E(x)+E(y) 还有: E(x)=∑pi*xi