数学思维修炼

Posted 2020-12-26 strick

最近想阅读一些数学方面的资料，但是又想和自己的工作联系上，因此就找到了这本《程序员的数学思维修炼（趣味解读）》，下面会对本书的知识点做个梳理。

1.2.6 数的阶乘

1.2.7 大整数

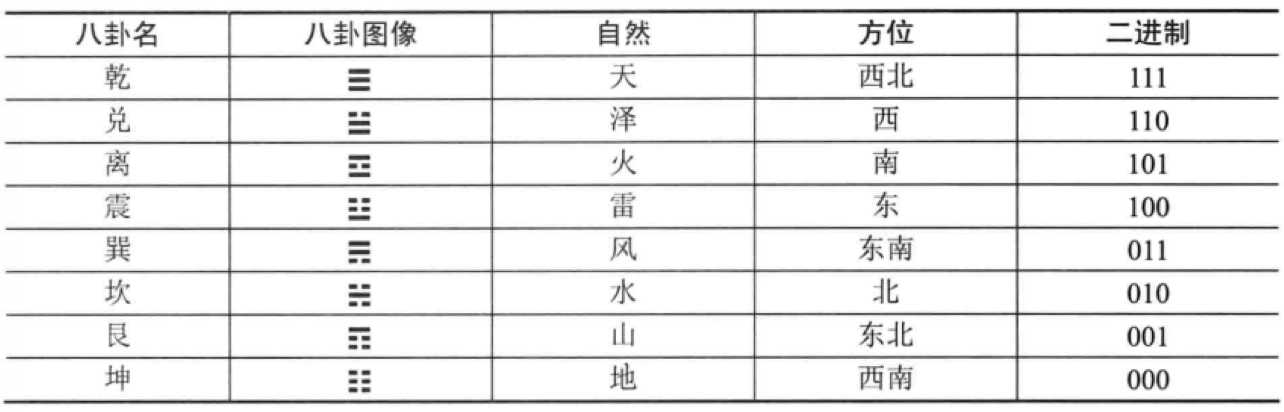
1.3.3 二进制运算

1.3.5 十进制和二进制之间的转换 以基数B再取余的方法

1.4 八进制、十六进制、六十进制

 

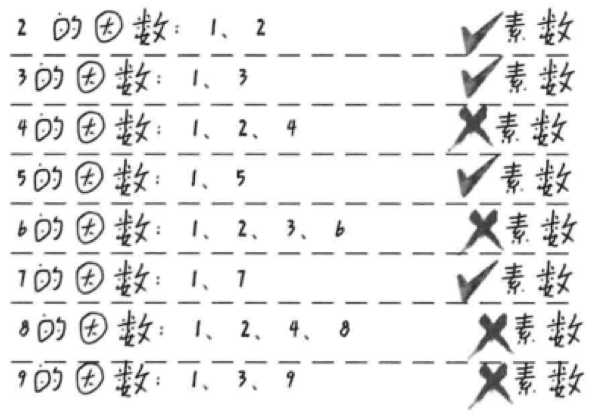
2.1.1 素数

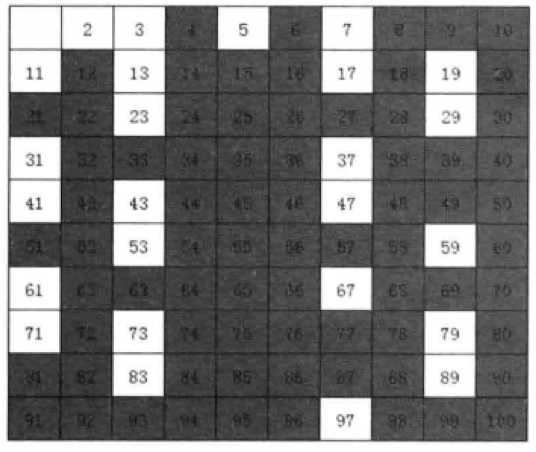
2.1.3 试除法（循环到√n即可），数学家筛选法，Eratosthenes寻找100以内的素数的算法：依次去除2、3、5、7的倍数的整数

2.1.4 素数定理

2.2.2 孪生素数

2.2.3 中国剩余定理

2.3 RSA算法，非对称加密，原理和实践

2.4 哥德巴赫猜想

2.5 梅森素数，2^p-1得到的是素数，其中p是素数

 

3.1.1 递归，按照先前定义的同类对象

3.1.2 德罗斯特效应（递归的一种视觉形式）

3.1.4 确定递归公式和边界条件

3.1.5 最大公约数，辗转相除法

3.2.2 递归的阶乘 

3.2.4 递归的基本思想：把规模大、难解决的问题变为规模小、易解决

3.3 汉诺塔 移动次数：2^n-1

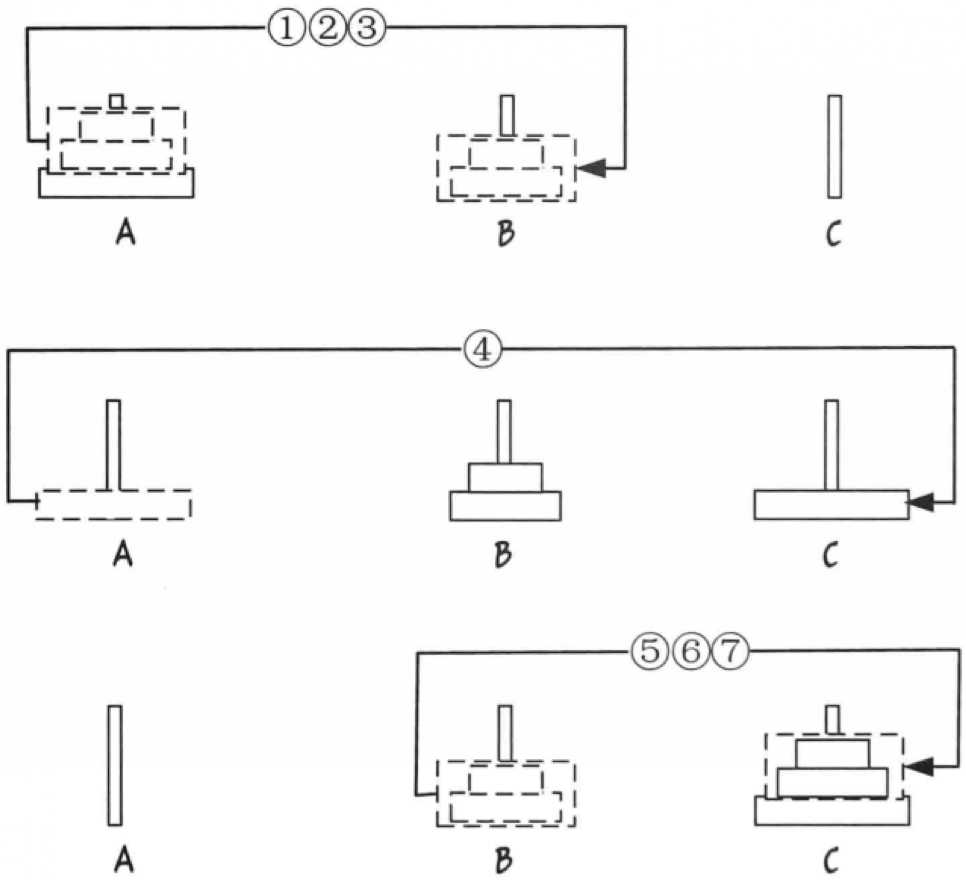
3.4 斐波那契数列

 

4.1 计数的两个问题：重复和遗漏

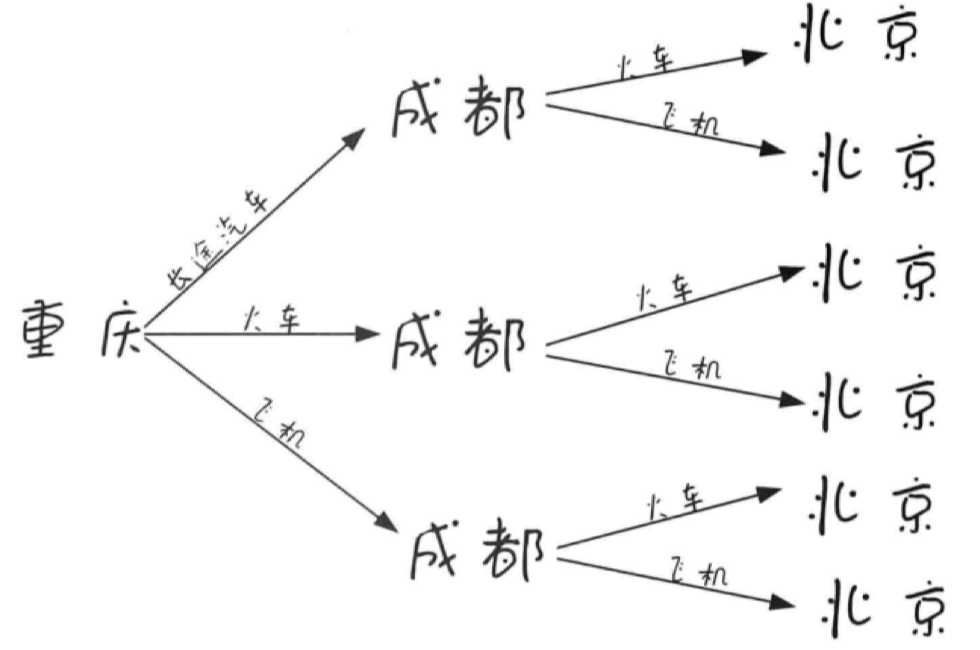
4.2.1 乘法原理，穷举法

4.2.2 核心是分步，每步只完成其中的一部分

4.2.3 棋子的放法

4.3.1 加法原理

4.3.2 核心是分类，每类只完成其中的一部分

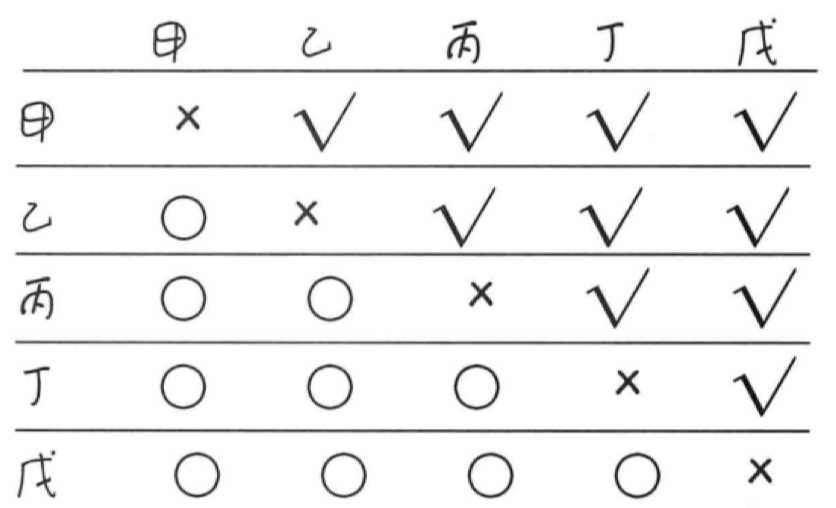
4.4.1 与顺序有关的是排列，枚举法。P.n^m=n*(n-1)...(n-m+1)

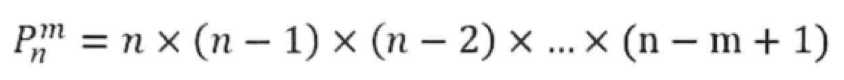
4.4.2 与顺序无关的是组合，C.n^m=P.n^m÷P.m^m

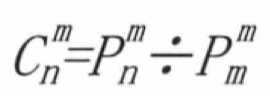
4.4.4 可重排列，电话号码和汽车牌照：n^m，n个不同元素的m种可重排列数

4.5 计算机字符编码，ASCII码、双字节、4字节和Unicode

4.6 密码长度和字符数

 

5.1.2 五条余数的性质

5.1.3 用余数进行分组

5.2 日历中的数学，计算星期几

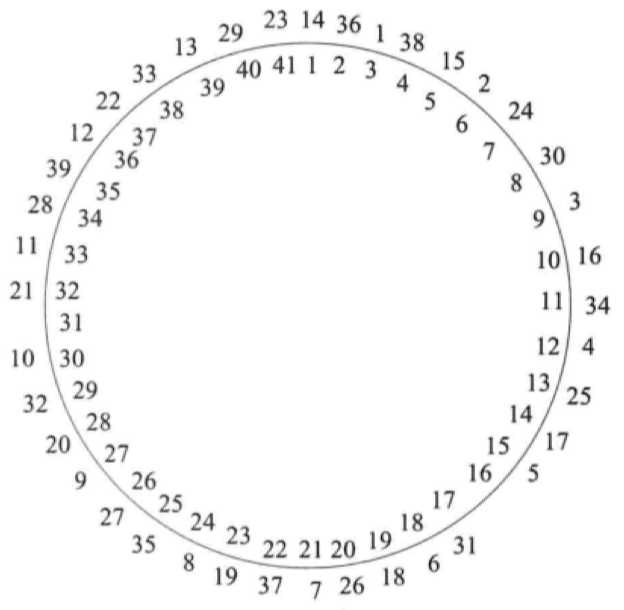
5.3 发牌魔术

5.4 通信中的奇偶校验，判断二进制代码中的位是1的个数，奇数或偶数

5.5.1 吕洞宾不能坐首位

5.5.3 约瑟夫环

5.6 智叟分牛

 

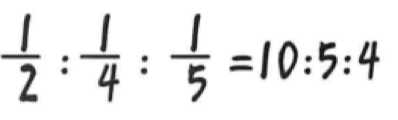
6.1 概率（或然率），抛硬币

6.1.4 必然事件和不可能事件

6.1.5 概率的四个基本性质

6.2 狄青的百枚钱币

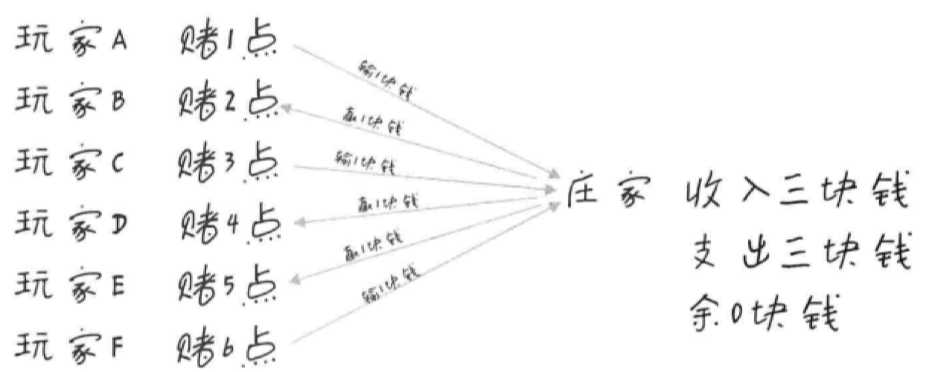
6.3 三个骰子的赌博

6.4 彩票

6.5 用概率估算鱼塘中鱼的重量

 

7.1.1 翻n番就是：基数 * 2^n

7.1.2 翻倍，在基数的基础上增加n倍：基数 * (n+1)

7.2.1 投资回报率：ROI = 年利润 / 投资总额 * 100%

7.2.2 单利：利润 = 投资额 * 利率 * 投资期，总收入 = 投资额 * (1 + 利率 * 投资期)

7.2.3 复利就是将上期利息加入本金中，然后一并计算利息的一种方法

7.2.5 信用卡还款

7.2.6 爱因斯坦的72法则，用72除以增长率（回报率）可快速估计出投资倍增或减半所需的时间

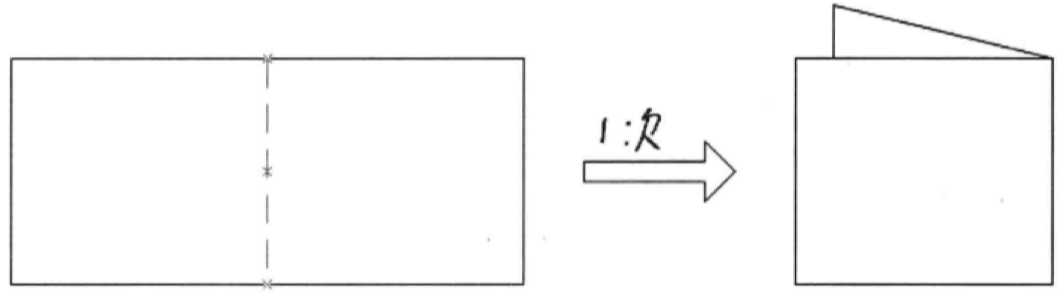
7.3 纸张对折：对折n次纸张厚度 = 原厚度 * 2^n

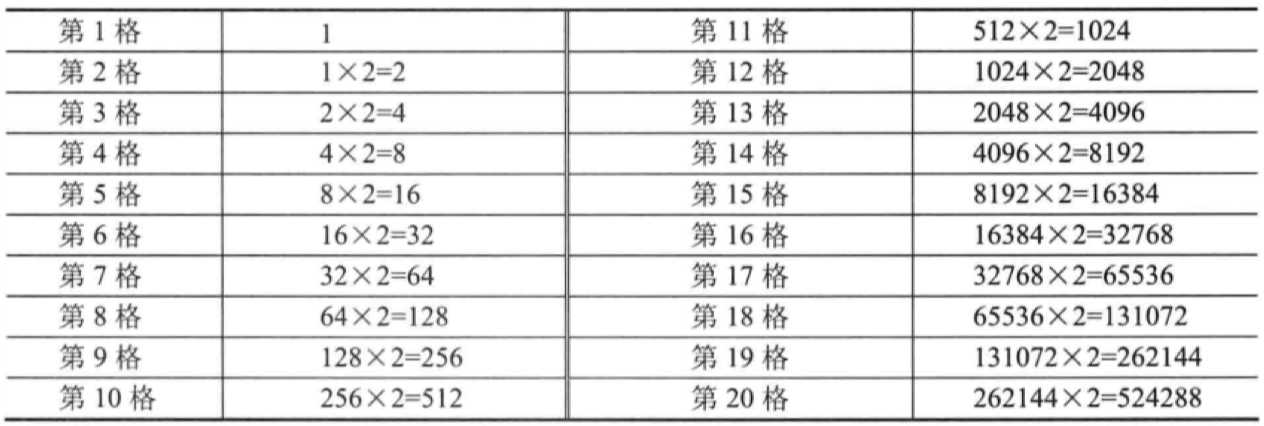
7.4 一棋盘的麦子：第n格麦粒数 = 2^n-1

7.5 折半法，假硬币

 

8.1.3 程序中的逻辑判断：程序 = 算法 + 数据，算法 = 逻辑 + 控制

8.2.1 命题：能判断真假的陈述句，例如中国位于亚洲

8.2.3 简单命题

8.2.4 复合命题

8.2.5 六种联接词：合取（且）、析取（或）、否定（非）、充分条件（如果...那么...）、必要条件（只有...才...）和充要条件（当且仅当）

8.3 布尔逻辑，逻辑或、逻辑与、逻辑非、逻辑异或

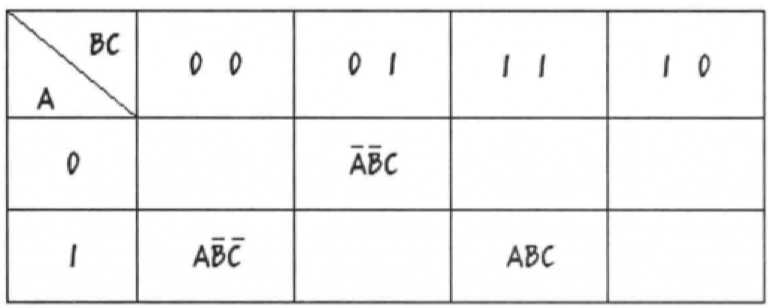
8.5 卡诺图：将此函数所有命题的真假组合以二维表的形式表示

 

9.1.1 演绎推理：通过演绎得出具体陈述或个别结论的过程

9.1.2 三段论，大前提、小前提和结论

9.1.3 选言推理，有两个前提的演绎推理，其中一个是选言命题（包含两个或多个的选择）

9.1.4 假言推理，根据假言命题的逻辑性质进行的推理：充分、必要和充分必要条件

9.1.5 关系推理，至少有一个关系判断，并按关系的逻辑性质进行推演

9.2.1 归纳推理：从个别性知识推出一般性结论，其中前提是真实的，结论未必为真，例如守株待兔

9.2.2 完全归纳推理：每一对象都具有或不具有某种属性，从而推出该类对象都具有或不具有某种属性

9.2.3 不完全归纳推理：某一类事物中的一部分对象具有或不具有某种属性，......，例如哥德巴赫猜想，所有大于5的奇数都可以分解为3个素数之和

 

10.1 花盆摆放

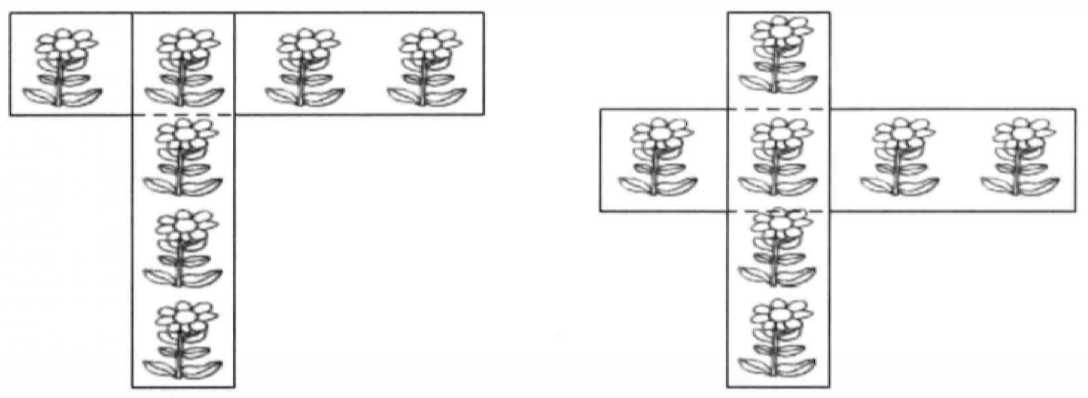
10.2 残缺的棋盘

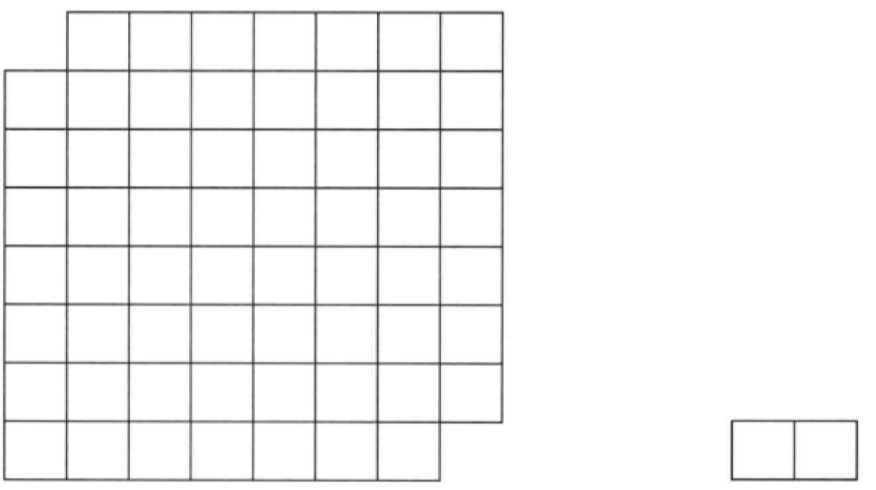
10.3 线条魔术

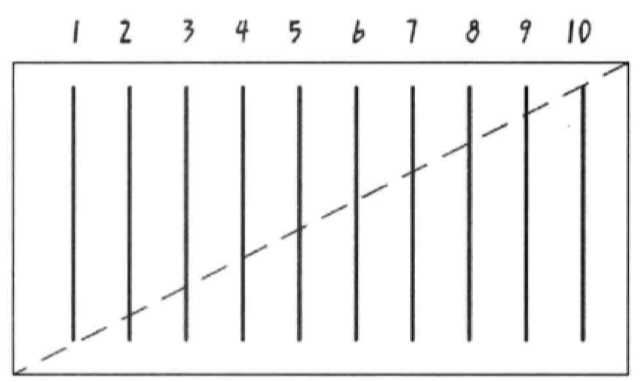
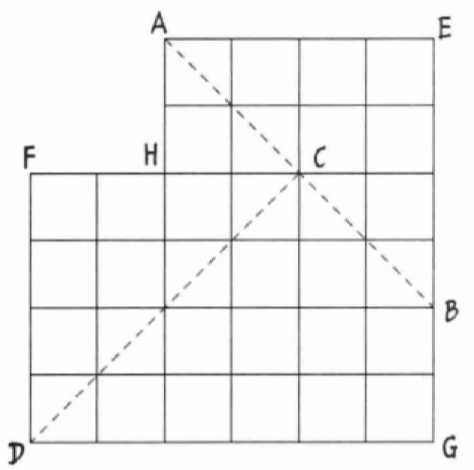
10.4 图形拼接，均分三角形和拼接正方形

 

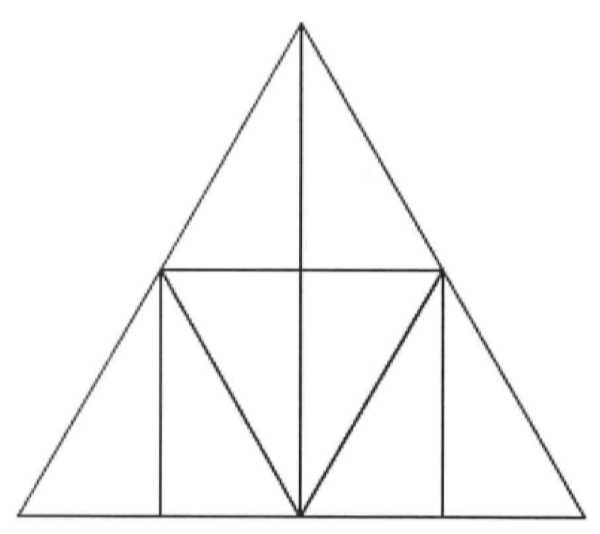
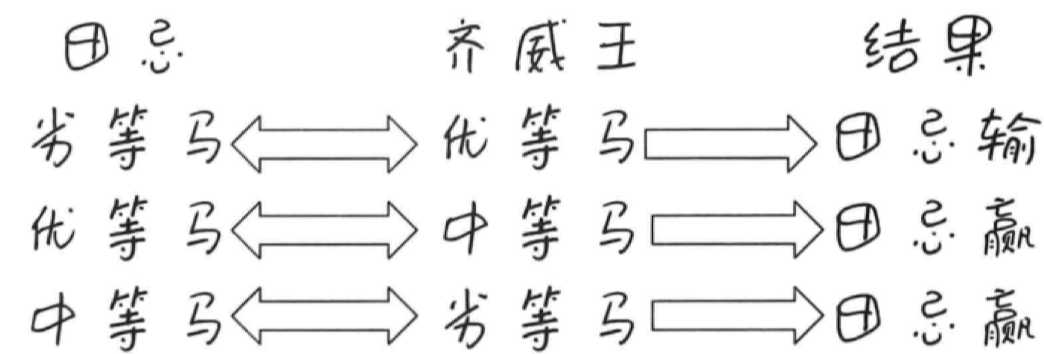
11.1 田忌赛马，统筹学目的：依据给定条件和目标，从众多方案中选择最佳方案

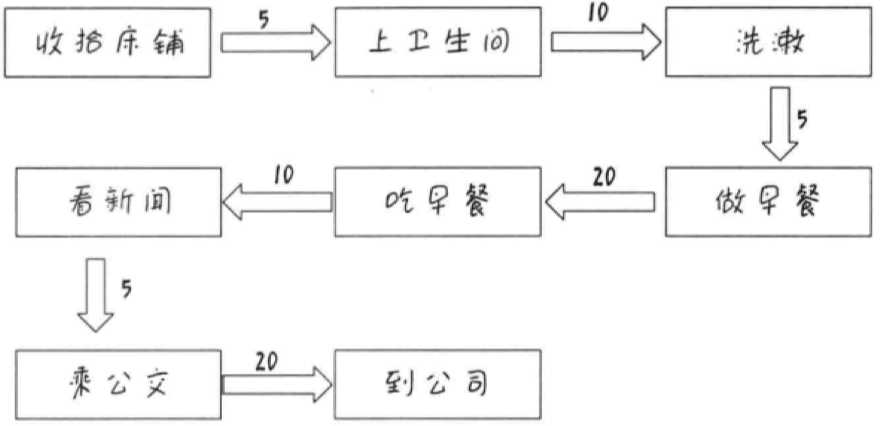
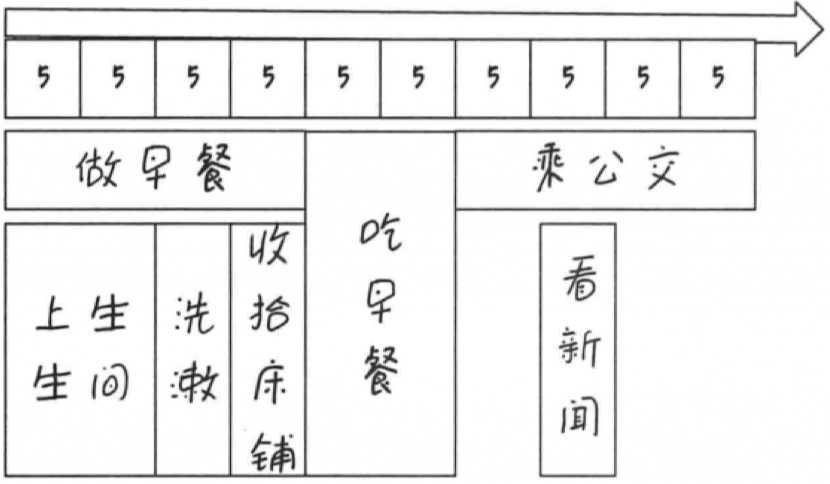
11.2 生活中的统筹规划

11.2.1 匆忙的早晨

11.2.2 节约运输成本

11.3 著名的动态规划求解问题：背包问题。