LCS(详解）

Posted 2020-12-26 moomcake

一，问题描述

给定两个字符串，求解这两个字符串的最长公共子序列（Longest Common Sequence）。比如字符串1：BDCABA；字符串2：ABCBDAB

则这两个字符串的最长公共子序列长度为4，最长公共子序列是：BCBA

 

二，算法求解

这是一个动态规划的题目。对于可用动态规划求解的问题，一般有两个特征：①最优子结构；②重叠子问题

①最优子结构

设 X=(x1,x2,.....xn) 和 Y={y1,y2,.....ym} 是两个序列，将 X 和 Y 的最长公共子序列记为LCS(X,Y)

找出LCS(X,Y)就是一个最优化问题。因为，我们需要找到X 和 Y中最长的那个公共子序列。而要找X 和 Y的LCS，首先考虑X的最后一个元素和Y的最后一个元素。

1）如果 xn=ym，即X的最后一个元素与Y的最后一个元素相同，这说明该元素一定位于公共子序列中。因此，现在只需要找：LCS(X_n-1，Y_m-1)

LCS(X_n-1，Y_m-1)就是原问题的一个子问题。为什么叫子问题？因为它的规模比原问题小。（小一个元素也是小嘛....）

为什么是最优的子问题？因为我们要找的是X_n-1 和 Y_m-1 的最长公共子序列啊。。。最长的！！！换句话说，就是最优的那个。（这里的最优就是最长的意思）

2）如果xn != ym，这下要麻烦一点，因为它产生了两个子问题：LCS(X_n-1，Y_m) 和 LCS(X_n，Y_m-1)

因为序列X 和 序列Y 的最后一个元素不相等嘛，那说明最后一个元素不可能是最长公共子序列中的元素嘛。（都不相等了，怎么公共嘛）。

LCS(X_n-1，Y_m)表示：最长公共序列可以在(x1,x2,....x(n-1)) 和 (y1,y2,...yn)中找。

LCS(X_n，Y_m-1)表示：最长公共序列可以在(x1,x2,....xn) 和 (y1,y2,...y(n-1))中找。

求解上面两个子问题，得到的公共子序列谁最长，那谁就是 LCS（X,Y）。用数学表示就是：

LCS=max{LCS(X_n-1，Y_m)，LCS(X_n，Y_m-1)}

由于条件 1)  和  2)  考虑到了所有可能的情况。因此，我们成功地把原问题 转化 成了 三个规模更小的子问题。

 

②重叠子问题

重叠子问题是啥？就是说原问题 转化 成子问题后，  子问题中有相同的问题。咦？我怎么没有发现上面的三个子问题中有相同的啊？？？？

OK，来看看，原问题是：LCS(X,Y)。子问题有 ?LCS(X_n-1，Y_m-1)    ?LCS(X_n-1，Y_m)    ?LCS(X_n，Y_m-1)

初一看，这三个子问题是不重叠的。可本质上它们是重叠的，因为它们只重叠了一大部分。举例：

第二个子问题：LCS(X_n-1，Y_m) 就包含了：问题?LCS(X_n-1，Y_m-1)，为什么？

因为，当X_n-1 和 Y_m 的最后一个元素不相同时，我们又需要将LCS(X_n-1，Y_m)进行分解：分解成：LCS(X_n-1，Y_m-1) 和 LCS(X_n-2，Y_m)

也就是说：在子问题的继续分解中，有些问题是重叠的。

 

由于像LCS这样的问题，它具有重叠子问题的性质，因此：用递归来求解就太不划算了。因为采用递归，它重复地求解了子问题啊。而且注意哦，所有子问题加起来的个数 可是指数级的哦。。。。

这篇文章中就演示了一个递归求解重叠子问题的示例。

那么问题来了，你说用递归求解，有指数级个子问题，故时间复杂度是指数级。这指数级个子问题，难道用了动态规划，就变成多项式时间了？？

呵呵哒。。。。

关键是采用动态规划时，并不需要去一 一 计算那些重叠了的子问题。或者说：用了动态规划之后，有些子问题 是通过 “查表“ 直接得到的，而不是重新又计算一遍得到的。废话少说：举个例子吧！比如求Fib数列。关于Fib数列，可参考：

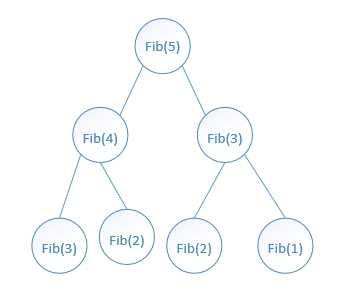
求fib(5)，分解成了两个子问题：fib(4) 和 fib(3)，求解fib(4) 和 fib(3)时，又分解了一系列的小问题....

从图中可以看出：根的左右子树：fib(4) 和 fib(3)下，是有很多重叠的！！！比如，对于 fib(2)，它就一共出现了三次。如果用递归来求解，fib(2)就会被计算三次，而用DP(Dynamic Programming)动态规划，则fib(2)只会计算一次，其他两次则是通过”查表“直接求得。而且，更关键的是：查找求得该问题的解之后，就不需要再继续去分解该问题了。而对于递归，是不断地将问题分解，直到分解为 基准问题(fib(1) 或者 fib(0))

 

说了这么多，还是要写下最长公共子序列的递归式才完整。借用网友的一张图吧：）

 

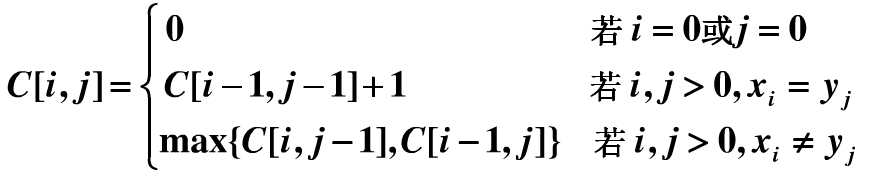
c[i,j]表示：(x1,x2....xi) 和 (y1,y2...yj) 的最长公共子序列的长度。（是长度哦，就是一个整数嘛）。公式的具体解释可参考《算法导论》动态规划章节

 

 

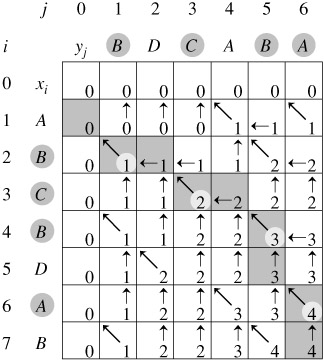
 1 #include<stdio.h>
 2 #include<string.h>
 3 #include<algorithm>
 4 #include<stack>
 5 #include<queue>
 6 #include<iostream>
 7 #include<map>
 8 #include<vector>
 9 #define Inf 0x3f3f3f3f
10 #define PI acos(-1.0)
11 using namespace std;
12 int str[1234];
13 int ans[1244];
14 int dp[1234][1234];
15 int len=1;
16 int main()
17 {
18     char str1[1234],str2[1234];
19     int len1,len2;
20     while(scanf("%s %s",&str1,&str2)!=-1){
21     len1=strlen(str1);
22     for(int i=len1;i>=1;i--)
23     {
24         str1[i]=str1[i-1];
25     }
26     len2=strlen(str2);
27     for(int i=len2;i>=1;i--)
28     {
29         str2[i]=str2[i-1];
30     }
31     memset(dp,0,sizeof(dp));
32     for(int i=1; i<=len1; i++)
33         for(int j=1; j<=len2; j++)
34         {
35              if(str1[i]==str2[j])
36              {
37                  dp[i][j]=dp[i-1][j-1]+1;
38              }
39              else{
40 
41                 dp[i][j]=max(dp[i][j-1],dp[i-1][j]);
42              }
43         }
44         printf("%d
",dp[len1][len2]);
45     }
46     return 0;
47 }

View Code