卡特兰数

Posted 2020-12-26 genius777

 卡特兰数是一种经典的组合数，经常出现在各种计算中，其前几项为 :

   1, 2, 5, 14, 42,
   132, 429, 1430, 4862, 16796,
   58786, 208012, 742900, 2674440, 9694845,
   35357670, 129644790, 477638700, 1767263190,
   6564120420, 24466267020, 91482563640, 343059613650, 1289904147324,
   4861946401452, ...

满足的递推公式

 

 

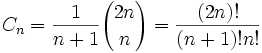
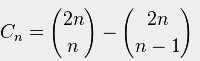
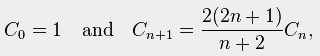
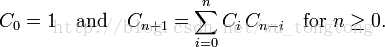
具体的应用

 

• Cn表示有n+1个叶子的二叉树的个数 
  

• Cn表示所有不同构的含n个分枝结点的满二叉树的个数（一个有根二叉树是满的当且仅当每个结点都有两个子树或没有子树）

• Cn表示所有在n × n格点中不越过对角线的单调路径的个数 
  一个单调路径从格点左下角出发，在格点右上角结束，每一步均为向上或向右 
  计算这种路径的个数等价于计算Dyck word的个数（同问题1）： 
  X代表“向右”，Y代表“向上”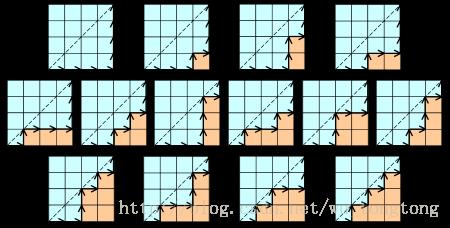 
  

• Cn表示通过连结顶点而将n + 2边的凸多边形分成三角形的方法个数 
  下图中为n = 4的情况： 
  

• Cn表示对{1, …, n}依序进出栈的置换个数 
  一个置换w是依序进出栈的当S(w) = (1, …, n), 
  其中S(w)递归定义如下：令w = unv，其中n为w的最大元素，u和v为更短的数列 
  再令S(w) =S(u)S(v)n，其中S为所有含一个元素的数列的单位元。

• Cn表示集合{1, …, n}的不交叉划分的个数. 其中每个段落的长度为2

• Cn表示用n个长方形填充一个高度为n的阶梯状图形的方法个数 
  下图为 n = 4的情况: 
  

总结最典型的四类应用：

（实质上却都一样，无非是递归等式的应用，就看你能不能分解问题写出递归式了）

1. 括号化问题。

   　　矩阵链乘： P=a1×a2×a3×……×an，依据乘法结合律，不改变其顺序，只用括号表示成对的乘积，试问有几种括号化的方案？(h(n)种)

2. 出栈次序问题。 
   　　一个栈(无穷大)的进栈序列为1,2,3,..n,有多少个不同的出栈序列? 
   　　 
   　　类似： 
   　　(1)有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票，另外n人只有10元钞票，剧院无其它钞票，问有多少中方法使得只要有10元的人买票，售票处就有5元的钞票找零？(将持5元者到达视作将5元入栈，持10元者到达视作使栈中某5元出栈) 
   　　 
   　　(2)在圆上选择2n个点,将这些点成对连接起来，使得所得到的n条线段不相交的方法数。 
   　　

3. 将多边行划分为三角形问题。 
   　　将一个凸多边形区域分成三角形区域的方法数? 
   　　 
   　　类似：一位大城市的律师在她住所以北n个街区和以东n个街区处工作。每天她走2n个街区去上班。如果她从不穿越（但可以碰到）从家到办公室的对角线，那么有多少条可能的道路？ 
   　　 
   　　类似：在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数? 
   　　 
   4.给顶节点组成二叉树的问题。 
   　　给定N个节点，能构成多少种形状不同的二叉树？ 
   　　先去一个点作为顶点,然后左边依次可以取0至N-1个相对应的,右边是N-1到0个,两两配对相乘,就是h(0)*h(n-1) + h(2)*h(n-2) +…+ h(n-1)h(0)=h(n)（能构成h(N)个）

总结

卡特兰数，可以起到对组合数求解的很大优化，但是一般来说（排除你是神犇的情况）卡特兰数在OI考试辨识出来是有一定难度的，我们一半可以通过打表找规律来推出某道题满足卡特兰数的性质，可见打表找规律能力很重要。

 

我们还是来看看一道题，题目传送门

---

 【代码实现】

 1 #include<cstdio>
 2 #include<cctype>
 3 #include<algorithm>
 4 using namespace std;
 5 inline void read(int &v)
 6 {
 7     int f;char ch;
 8     while(!isdigit(ch=getchar())&&ch!=‘-‘); ch==‘-‘?(f=-1,v=0):(f=1,v=ch-‘0‘);
 9     while(isdigit(ch=getchar())) v=v*10+ch-‘0‘;v=v*f;
10 }
11 const int N=2e6+5;
12 int low[N],p[N],sum[N],n,mod,cnt,ans=1;
13 bool vis[N];
14 void get_prime()
15 {
16     for(int i=2;i<=2*n;i++)
17     {
18         if(!vis[i]) p[++cnt]=i,low[i]=i;
19         for(int j=1;j<=cnt;j++)
20         {
21             if(p[j]*i>2*n) break;
22             vis[p[j]*i]=1,low[p[j]*i]=p[j];
23             if(p[j]%i==0) break;
24         }
25     }
26 }
27 void get_sum(int v,int x)
28 {
29     while(v>1)
30     {
31         sum[low[v]]+=x;
32         v=v/low[v];
33     }
34 }
35 int main()
36 {
37     read(n),read(mod);
38     get_prime();
39     for(int i=1;i<=n;i++) get_sum(i,-1);
40     for(int i=n+2;i<=2*n;i++) get_sum(i,1);
41     for(int i=1;i<=2*n;i++) 
42     for(int j=1;j<=sum[i];j++) ans=1ll*ans*i%mod;
43     printf("%d",ans);
44     return 0;
45 }