第一次接触状压DP

Posted 2020-12-26 sky-zxz

状压DP入门及理解

*（另类的暴力）*

     一般状态数不多的时候就会开数组，但是有的状态并不好表示，于是，状压DP就产生了。

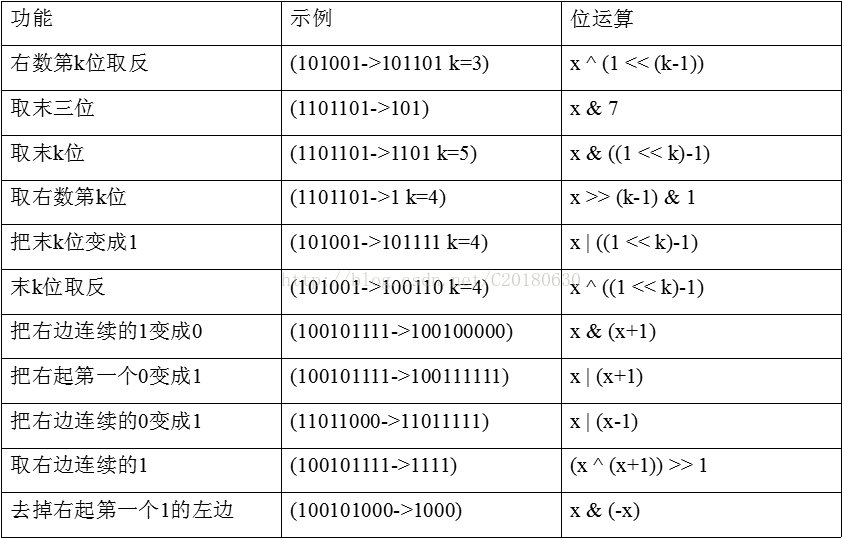
    状压DP应该是分两类的，一类是压缩状态，另一类是舍弃状态。    我感觉初学状压DP难就难在二进制运算的应用，了解二进制运算符就显得十分重要。

    所以我们先看下表，如果有不会二进制简单应用的请点击https://blog.csdn.net/sinat_35121480/article/details/53510793（神犇请忽略...）

 

 

下面就可以看题了：

对于状压压缩，入门题[USACO06NOV]玉米田和Corn Fields[SCOI2005]互不侵犯，思路基本上相同。

[USACO06NOV]玉米田Corn Fields

https://www.lydsy.com/JudgeOnline/problem.php?id=1725

我自己做了这两个题有两点体会，如下：

第一点（第一题）：我们可以通过循环预处理出所有的状态，再在动态规划的过程中判断状态是否可行，方案数累加即可。

这样来，动态规划的方程就很好推出来了（初学者可能有点困难）。

 

F[ I ][ j ] 表示前I行，第I行状态为J的方案数，J存的是状态，用二进制表示。

 

代码如下：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<bitset>
using namespace std;//前 i 行  //当前行 状态为j的方案数
int n,m,a[15][15],g[1<<12],f[15][1<<12],mod=1e8;
int check(int x)
{
    if(!((x<<1)&x)&&!((x>>1)&x))
    return 1;
    else
    return 0;
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    for(int j=1;j<=m;j++)
    scanf("%d",&a[i][j]);
    for(int i=1;i<=n;i++)
    for(int j=1;j<=m;j++)//转化成二进制
    g[i]=(g[i]<<1)+a[i][j];
    for(int i=0;i<(1<<m);i++)
    if(check(i)&&((i&g[1])==i))//后者表示在可以种植的地方选择（全选/部分/不选)地方去种，有点子集的感觉。
    f[1][i]=1;
        for(int i=2;i<=n;i++)//第i行
        {
            for(int j=0;j<(1<<m);j++)//第i行状态为J
            {
             if(check(j)&&((j&g[i])==j))
             for(int k=0;k<(1<<m);k++)//第i-1行状态为k
             {
             if(check(k)&&((k&g[i-1])==k)&&(!(k&j)))
             f[i][j]+=f[i-1][k],f[i][j]%=mod;
             }
            }
        }
    int ans=0;
    for(int i=0;i<(1<<m);i++)
    ans+=f[n][i],ans%=mod;
    printf("%d",ans%mod);
    return 0；
}

[SCOI2005]互不侵犯

https://www.lydsy.com/JudgeOnline/problem.php?id=1087

第二点（第二题）：我们可以通过DFS搜索出所有符合情况的方案记录下来再进行动态规划。

DFS过程中如果搜到行的尽头，我们就保存状态再返回，否则就进行下一步搜索。

搜索分两种状态：1.当前格子不放国王，搜索下一个格子  2.当前格子放国王，就得跳过下一个格子搜索。（代码中有特别注释）

我们先不要管在列方向上的约束，只管每一行的国王不能放在一起，每一列的国王不能放在一起那是下面要考虑的问题。

当所有满足条件的行的状态都搜索出来之后，就可以动态规了，中间剔除列上不符要求的状态。

动态规划方程也跟上题的差不多：

F[ I ][ J ] [ K ] 表示前 I 行 ，第 i 行状态为J  总共选了K个国王的方案数。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#define ll long long int
using namespace std;
ll n,t,top,sum[2000],zt[2000],f[20][1000][300],ans;//位置  状态   选了几个
void dfs(ll z,ll s,ll ci)
{
    if(ci>=n)
    {
        top++;
        zt[top]=z;
        sum[top]=s;
        return;
    }
    dfs(z,s,ci+1);//不选
    dfs(z+(1<<ci),s+1,ci+2);//选
}
int main(){
    scanf("%lld%lld",&n,&t);
    dfs(0,0,0);
    for(ll i=1;i<=top;i++)f[1][i][sum[i]]=1;
    for(ll i=2;i<=n;i++)
      for(ll j=1;j<=top;j++)
        for(ll k=1;k<=top;k++)
        {
            if(zt[j]&zt[k])continue;
            if((zt[j]<<1)&zt[k])continue;
            if((zt[k]<<1)&zt[j])continue;
            for(ll q=sum[j];q<=t;q++){
                f[i][j][q]+=f[i-1][k][q-sum[j]];
                //前i行 第i行状态为j  有q个国王的方案数。
            }
        }
    for(ll i=1;i<=top;i++)
    ans+=f[n][i][t];
    printf("%lld",ans);
    return 0;
}

嗯，这道题是右上角的大佬教我的。

我对于状压DP的理解刚刚入门，可能还有很多说的不妥当的地方希望各位神犇评论告知。

2018-07-28

19:17:14