归并排序

Posted 2020-12-25 wuqinglong

概念

归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

将两个的有序数列合并成一个更大的有序数列，我们称之为"归并"。

归并排序(Merge Sort)就是利用归并思想对数列进行排序。根据具体的实现，归并排序包括"从上往下"和"从下往上"2种方式。

1. 从下往上的归并排序
   1. 将待排序的数列分成若干个长度为1的子数列。
   2. 将这些数列两两合并，得到若干个长度为2的有序数列。
   3. 再将这些数列两两合并；得到若干个长度为4的有序数列。
   4. 再将它们两两合并；直到合并成一个数列为止。
2. 从上往下的归并排序：它与"从下往上"在排序上是反方向的。
   1. 分解 -- 将当前区间一分为二，即求分裂点 mid = (low + high)/2;
   2. 求解 -- 递归地对两个子区间a[low...mid] 和 a[mid+1...high]进行归并排序。递归的终结条件是子区间长度为1。
   3. 合并 -- 将已排序的两个子区间a[low...mid]和 a[mid+1...high]归并为一个有序的区间a[low...high]。

两种排序的区别可以参考下面图片：

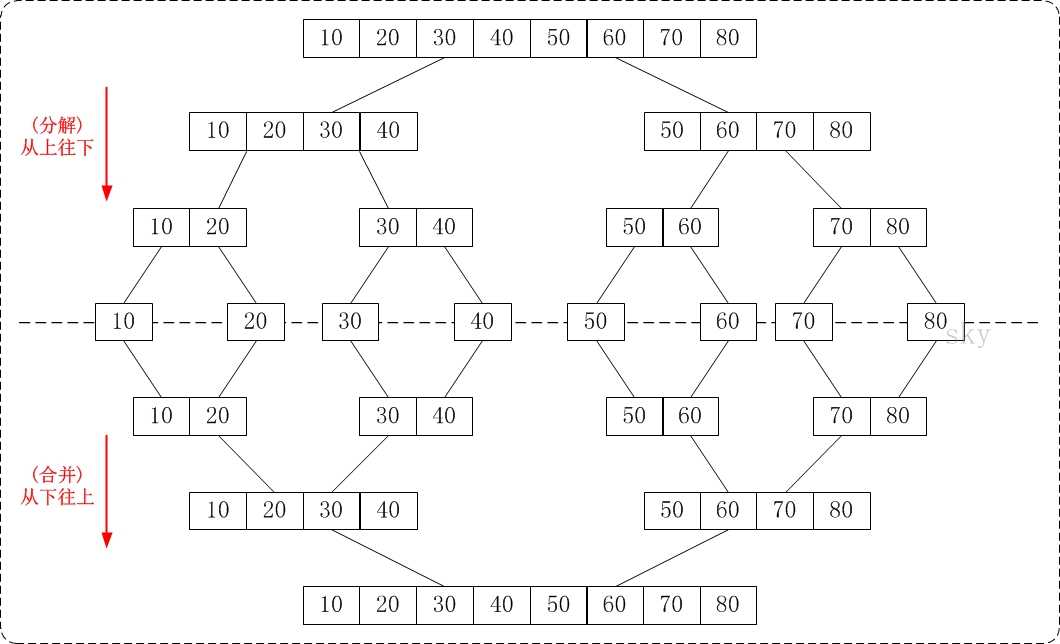
分析

• 时间复杂度：O(nlog₂n)，这是基于比较的排序算法所能达到的最高境界。
• 空间复杂度：需要 O(n) 的辅助空间，而与之效率相同的快排和堆排分别需要O(logn)和O(1)的辅助空间，在同类算法中归并排序的空间复杂度略高。
• 是一种效率高且稳定的算法。

代码说明

基础归并

将两个数组合并为进行一次合并

@Test
public void mergeSorBase() {

    // 初始化数组
    // 两个子数组([0,2]和[3,5])都是有序的
    int[] array = {4,5,6,2,3,9};
    int[] temp = new int[array.length];

    // 数组参数
    int left = 0;
    int right = array.length - 1;
    int mid = (left + right) / 2;

    // 辅助循环
    int i = left; // 左边数组的第一个元素
    int j = mid + 1; // 右边数组的第一个元素
    int index = 0; // 临时数组下标

    // 循环比较两个数组的值, 直到其中一个数组遍历结束
    while (i <= mid && j <= right) {
        if (array[i] < array[j])
            temp[index++] = array[i++];
        else
            temp[index++] = array[j++];
    }

    // 取出左边数组剩余的元素
    while (i <= mid) {
        temp[index++] = array[i++];
    }

    // 取出右边数组剩余的元素
    while (j <= right) {
        temp[index++] = array[j++];
    }

    // 把临时数组中的值填充到原数组
    for (int k = 0; k < index; k++) {
        array[left + k] = temp[k];
    }

    // 打印数组元素
    for (int t : array) {
        System.out.print(t);
    }

}

 

从上往下归并

所有的归并排序最终都依赖于上面的基础归并

@Test
public void mergeSort() {

    // 初始化数组
    int[] array = {4,5,1,6,2,3,7,9};
    sort(array, 0, array.length - 1);
    // 打印数组元素
    for (int t : array) {
        System.out.print(t);
    }

}

private void sort(int[] array, int left, int right) {

    if (left >= right) return;

    int mid = (left + right) / 2;

    // 排序左边的
    sort(array, left, mid);

    // 排序右边的
    sort(array, mid + 1, right);

    // 合并两边数组
    merge(array, left, mid, right);
}

private void merge(int[] array, int left, int mid, int right) {
    int[] temp = new int[array.length];

    int i = left;
    int j = mid + 1;
    int ti = 0;

    // 合并数组, 会有一个数组会剩余元素
    while (i <= mid && j <= right) {
        if (array[i] < array[j]) {
            temp[ti++] = array[i++];
        } else {
            temp[ti++] = array[j++];
        }
    }

    // 如果左边剩余元素
    while (i <= mid) {
        temp[ti++] = array[i++];
    }

    // 如果右边剩余元素
    while (j <= right) {
        temp[ti++] = array[j++];
    }

    // 将临时数组的值, 对应到原数组
    for (int k = 0; k < ti; k++) {
        array[left + k] = temp[k];
    }

}

 

 

参考：https://www.cnblogs.com/skywang12345/p/3602369.html