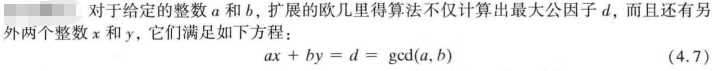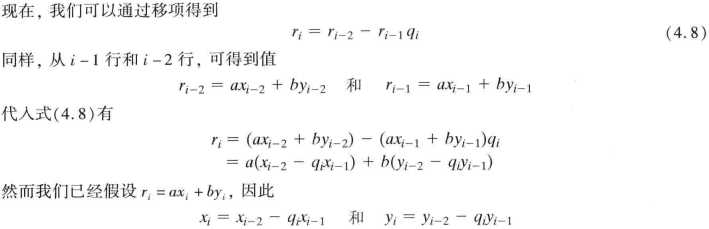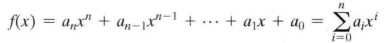AES-128加密过程中的S盒构造
Posted junbo20141201
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了AES-128加密过程中的S盒构造相关的知识,希望对你有一定的参考价值。
文档引用了《密码编码学与网络安全--原理和实践》里边的推导过程,如有不妥,请与我联系修改。
文档《FIPS 197》高级加密标准AES,里边有个S盒构造,涉及到了数论和有限域的一些概念,一脸懵逼,所以贱贱的研究了下,花了好久时间。
在网上找的S盒构造的详细步骤总是缺了点什么,要么步骤不详细,要么只贴了程序,难以搞清楚由几个基本概念一步一步推导出最终的S盒。最后,还是《密码编码学与网络安全--原理和实践》这本书讲得比较详细。教材果然还是经过精雕细琢过的,符合大部分人的认知过程。
这篇文章其一是记录下来这个学习步骤,其二是希望我的这篇能够更详细些。
先贴出来《FIPS 197》中对S盒构造的描述步骤:

就这两条。实际上是三个步骤,《密码编码学与网络安全--原理和实践》教材里会讲得更详细些。

一下都按照《密码编码学与网络安全--原理和实践》教材里边的三个步骤进行推导。
步骤1、3都比较浅显,即使没有数论和有限域概念,一样可以编程写出来。
步骤一:
根据行标号和列标号组合成16X16的二维数组,行标号作为高4bit,列标号作为低4bit;
生成代码如下:
1 for(i=0;i<0x10;i++)
2 {
3 for(j=0;j<0x10;j++)
4 {
5 s_box_ary[i][j] = ((i<<4)&0xF0) + (j&(0xF));
6 }
7 }
代码产生的数组:
1 0 1 2 3 4 5 6 7 8 9 A B C D E F
2 0 0 1 2 3 4 5 6 7 8 9 a b c d e f
3 1 10 11 12 13 14 15 16 17 18 19 1a 1b 1c 1d 1e 1f
4 2 20 21 22 23 24 25 26 27 28 29 2a 2b 2c 2d 2e 2f
5 3 30 31 32 33 34 35 36 37 38 39 3a 3b 3c 3d 3e 3f
6 4 40 41 42 43 44 45 46 47 48 49 4a 4b 4c 4d 4e 4f
7 5 50 51 52 53 54 55 56 57 58 59 5a 5b 5c 5d 5e 5f
8 6 60 61 62 63 64 65 66 67 68 69 6a 6b 6c 6d 6e 6f
9 7 70 71 72 73 74 75 76 77 78 79 7a 7b 7c 7d 7e 7f
10 8 80 81 82 83 84 85 86 87 88 89 8a 8b 8c 8d 8e 8f
11 9 90 91 92 93 94 95 96 97 98 99 9a 9b 9c 9d 9e 9f
12 a a0 a1 a2 a3 a4 a5 a6 a7 a8 a9 aa ab ac ad ae af
13 b b0 b1 b2 b3 b4 b5 b6 b7 b8 b9 ba bb bc bd be bf
14 c c0 c1 c2 c3 c4 c5 c6 c7 c8 c9 ca cb cc cd ce cf
15 d d0 d1 d2 d3 d4 d5 d6 d7 d8 d9 da db dc dd de df
16 e e0 e1 e2 e3 e4 e5 e6 e7 e8 e9 ea eb ec ed ee ef
17 f f0 f1 f2 f3 f4 f5 f6 f7 f8 f9 fa fb fc fd fe ff
本文重点叙述步骤2的推导。
步骤二:
这里边有三个概念:有限域、GF(2^8)、逆。
有限域:我的理解是,有一些元素构成了一个集合,集合中的一个或多个元素,进行某种运算,所得的结果仍然是集合中的元素。 元素,可以是具体的数字,也可以是字母,或是表达式,等等;某种运算,可以是加减乘除,或者逻辑运算,或者求余,或者是这几种运算的组合,等等。 这个定义当然很不严格,但是我觉得对于理解这个S盒推导够用了。
GF(2^8):GF()是代表一个有限域,2^8=256,是指这个有限域内的元素的个数,即256个。
举个是有限域的集合的例子吧。
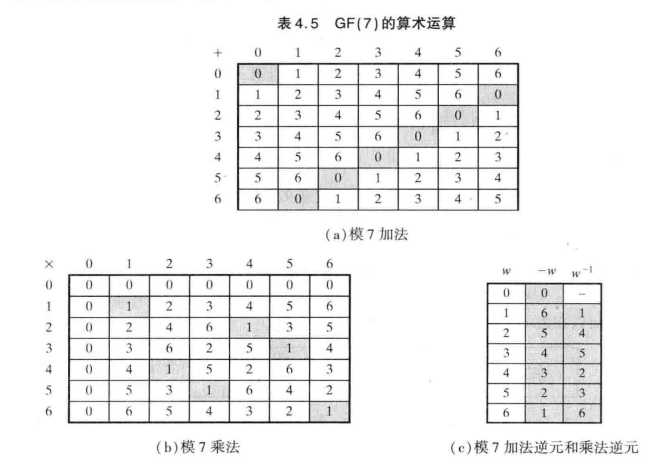
GF(7)={0,1,2,3,4,5,6},它是关于任意两个元素的相加/乘积模7运算的有限域。特点是任意两个元素相加/乘积,对7取余数,这个余数仍然在GF(7)内。
截取《密码编码学与网络安全--原理和实践》中的例子:
此外,这个GF(7)的7叫做阶,特点是阶与域内的元素都互素(互质)。
在计算机中,一个字节是8位,0~255刚好是一个字节所能代表的所有数字,但是呢,GF(256),256对于0~255内的元素并不是每个都互素(互质),当以251为模时,251~255又不能用,造成浪费,所以不能直接使用上边的计算形式。但是我们还得必须用0~255这256个整数作为一个集合,通过某种运算构成有限域,所有只能把研究重点放在“某种运算”上。可能是为了区分GF(256),所以用GF(2^8)。
逆:乘法逆元。定义:GF(p), (a)、(b)、(a-1)都在GF(p)内,其中(a)、(a-1)互为乘法逆元,则有:[(a) X (a-1)] mod p = 1;
第二个步骤,就是 在步骤一得到的数组基础上,对每个元素 在 GF(2^8)有限域上求解出乘法逆元,在原位置替换该元素。
如何求解有限域上的逆元?《密码编码学与网络安全--原理和实践》中从欧几里得算法开始做知识铺垫,到扩展欧几里得算法。我们可以得出求乘法逆元的一个程序上可实现的方法。
d=gcd(a,b),d是a和b的最大公约数,或者叫最大公因子。求解步骤:
1、定义变量:r0, r1, r2
2、赋初值r0=a;r1=b;
3、求解r0、r1的余数:r3=r0 Mod r1;
4、更新变量:r0=r1;r1=r2;
5、从3开始重复,一直到求解的余数r1是0结束。
6、r0就是要求解的最大公约数。
long gcd(long a, long b)
{
long tmp;
while(b)
{
tmp=a;
a=b;
b=tmp%b;
}
return a;
}
欧几里得算法的关键是gcd(a,b)=gcd(b,(a mod b));为什么能成立?
可以证明:
当a>b,就有,a=q1 * b + r1,r1 = a - q1 * b;
假设 d=gcd(a,b),那么d分别是a和b的最大公因子,记作:d|a,d|b,所以:d|(a-q1 * b)=d|r1
所以有d=gcd(b,r1)=gcd(b, (a mod b));
《密码编码学与网络安全--原理和实践》里边讲解会更详细:
扩展欧几里得算法的计算步骤同欧几里得算法的步骤相似,由一个公式迭代计算,一直达到某个条件成立结束迭代,返回结果。
扩展欧几里得算法用来求解乘法逆元,为什么?
上边已经有了公式:[(a) * (a-1)] mod p = 1;
可以等效变换成:p * x + 1 = (a) * (a-1)
========> - p * x + (a) * (a-1) = 1
与ax+by=1的形式是不是很像?
与ax+by=gcd(a,b)=1的形式是不是很像?
gcd(a,b)=1,就是a、b互素即可。
可以看出,可以运用欧几里得算法的步骤计算乘法逆元,但是怎么计算呢?
这点我还是照搬《密码编码学与网络安全--原理和实践》里边的讲解步骤吧,我觉得不会比他讲得更好了。
就是这样,初始条件:(R-1) = a; R0=b; (X-1)=1;X0=0;(Y-1)=0;Y0=1;
迭代步骤:Rn=(Rn-2) Mod (Rn-1);Qn = [(Rn-2) /(Rn-1)] {(Rn-2) /(Rn-1)的商};Xn = (Xn-2) - (Xn-2) ;Yn = (Yn-2) - (Yn-2) 。
终止条件:Rn=1时,计算出来的Yn即是结果。
如果结果为负数,需要加上模值变为正数。
代码如下:
long multiplicativeInverse(long a, long b)
{
long r0,r1,r2,q1,x0,x1,x2,y0,y1,y2;
long d = gcd(a,b);
if((d!=1)&&(d!=-1))
{
printf("a、b不互质
");
return -1;
}
r0=a;
r1=b;
x0=1;
y0=0;
x1=0;
y1=1;
if((b==1)||(b==-1))
{
y2=y1;
}
while((r1!=1)&&(r1!=-1))
{
q1=r0/r1;
r2=r0%r1;
x2=x0-q1*x1;
y2=y0-q1*y1;
r0=r1;
r1=r2;
x0=x1;
x1=x2;
y0=y1;
y1=y2;
}
if(y2 < 0)
{
y2=a+y2;
}
return y2;
}
回归到GF(2^8)有限域,需要找到“某种运算”,使GF(2^8)有限域成立。这种运算是多项式除法运算。
多项式如下形式:
我们可以把GF(2^8)有限域内的每一个元素,按照下列方式写成多项式的形式:
设 字节a ∈ GF(2^8),写成二进制的形式a=b7b6b5b4b3b2b1b0,用bn代表a的每一位,其中n是二进制数中的位置;
那么,bn当作系数,n作为变量x的指数;
可以把一个字节写成:
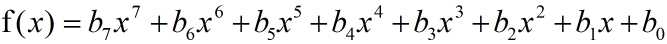
这种形式。
举例:
0x9A=(b)10011010,写成多项式形式:x^7+x^4+x^3+x。
多项式除法运算,计算规则:
1、遵循代数基本规则中的普通多项式运算规则;
2、系数运算遵循以2为模的加法和乘法运算;(原话是:系数运算以p为模,即遵循有限域Zp上的运算规则);
3、如果乘法运算的结果是次数大于7(原文:n-1)的多项式,那么必须将其除以某个次数为8(原文:n)的即约多项式m(x)并取余式,对于多项式f(x),这个余数可表示为:即r(x) = f(x) mod m(x)。
高级加密标准AES使用有限域GF(2^8)上的运算,其中即约多项式m(x)=x^8 + x^4 + x^3 + x + 1;
举例:
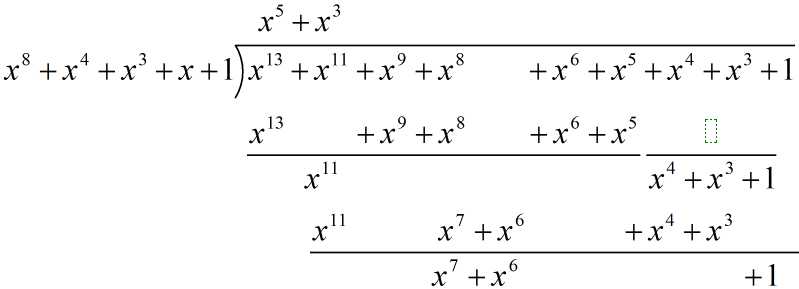
m(x)=x^8 + x^4 + x^3 + x + 1;
f(x) =x^6 + x^4 + x^2 + x + 1;g(x) =x^7 + x + 1;
f(x) * g(x) = (x^6 + x^4 + x^2 + x + 1) * (x^7 + x + 1)
= x^13 + x^11 + x^9 + x^8 + x^7
+ x^7 + x^5 + x^3 + x^2 + x
+ x^6 + x^4 + x^2 + x + 1
= x^13 + x^11 + x^9 + x^8 + x^6+ x^5 + x^4 + x^3 + 1
r(x) = [f(x) * g(x)] mod m(x) => m(x) * q(x) + r(x) = f(x) * g(x):
q(x) = x^5 + x^3;r(x) = x^7 + x^6 + 1。
上文已经讲到:扩展欧几里得算法用来求解乘法逆元。
(b-1)*b mod a = 1; => ax+by=1=gcd(a, b)
把a、b用多项式替代,形式如下:
b-1(x) * b(x) mod m(x) = 1 => m(x)v(x) + b(x)w(x) = 1 = gcd(m(x), b(x))
直接引用上边求乘法逆元的步骤,用多项式直接替代数值计算:
重述如下:
1、把带求解的字节变换成多项式形式b(x);
2、初始条件:
(R-1) = m(x); R0=b(x);
(v-1)(x)=1; v0(x)=0;
(w-1)(x)=0; w0(x)=1;
3、迭代步骤:
Rn(x)=(Rn-2)(x) Mod (Rn-1)(x);
Qn(x) = [(Rn-2)(x) / (Rn-1)(x)] 即:{(Rn-2) /(Rn-1)的商};
vn(x) = (vn-2)(x) - Qn(x)*(vn-2)(x) ;
wn(x) = (wn-2)(x) - Qn(x)*(wn-2) 。
4、终止条件:
Rn(x)=1时,计算出来的wn(x)即是结果多项式。
5、把wn(x)变换回字节。
上述步骤中,需要专门的多项式乘法、多项式除法、多项式求余运算的实现函数。
多项式乘法函数:
//GF(2^8)的多项式乘法 uint16_t polynomialMutil(uint8_t a, uint8_t b) { uint16_t tmp[8]={0}; uint8_t i; for(i=0;i<8;i++) { tmp[i] = (a<<i)*((b>>i)&0x1); } tmp[0] = tmp[0] ^ tmp[1] ^ tmp[2] ^ tmp[3] ^ tmp[4] ^ tmp[5] ^ tmp[6] ^ tmp[7]; return tmp[0]; }
多项式除法函数:
//找到最高位 uint8_t findHigherBit(uint16_t val) { int i=0; while(val) { i++; val = val>>1; } return i; } //GF(2^8)的多项式除法 uint8_t gf28_div(uint16_t div_ed, uint16_t div, uint16_t *remainder) { uint16_t r0=0; uint8_t qn=0; int bitCnt=0; r0=div_ed; bitCnt = findHigherBit(r0)-findHigherBit(div); while(bitCnt>=0) { qn = qn | (1<<bitCnt); r0 = r0 ^ (div<<bitCnt); bitCnt = findHigherBit(r0)-findHigherBit(div); } *remainder = r0; return qn; }
多项式的扩展欧几里得算法:
//GF(2^8)多项式的扩展欧几里得算法 uint8_t extEuclidPolynomial(uint8_t a, uint16_t m) { uint16_t r0, r1, r2; uint8_t qn, v0, v1, v2, w0, w1, w2; r0=m; r1=a; v0=1; v1=0; w0=0; w1=1; while(r1!=1) { qn=gf28_div(r0, r1, &r2); v2=v0^polynomialMutil(qn, v1); w2=w0^polynomialMutil(qn, w1); r0=r1; r1=r2; v0=v1; v1=v2; w0=w1; w1=w2; } return w1; }
至此,S盒变换的第二步骤实现完成。
根据 扩展欧几里得算法,得到的中间状态的S盒如下:
0 1 2 3 4 5 6 7 8 9 A B C D E F 0 0 1 8d f6 cb 52 7b d1 e8 4f 29 c0 b0 e1 e5 c7 1 74 b4 aa 4b 99 2b 60 5f 58 3f fd cc ff 40 ee b2 2 3a 6e 5a f1 55 4d a8 c9 c1 a 98 15 30 44 a2 c2 3 2c 45 92 6c f3 39 66 42 f2 35 20 6f 77 bb 59 19 4 1d fe 37 67 2d 31 f5 69 a7 64 ab 13 54 25 e9 9 5 ed 5c 5 ca 4c 24 87 bf 18 3e 22 f0 51 ec 61 17 6 16 5e af d3 49 a6 36 43 f4 47 91 df 33 93 21 3b 7 79 b7 97 85 10 b5 ba 3c b6 70 d0 6 a1 fa 81 82 8 83 7e 7f 80 96 73 be 56 9b 9e 95 d9 f7 2 b9 a4 9 de 6a 32 6d d8 8a 84 72 2a 14 9f 88 f9 dc 89 9a a fb 7c 2e c3 8f b8 65 48 26 c8 12 4a ce e7 d2 62 b c e0 1f ef 11 75 78 71 a5 8e 76 3d bd bc 86 57 c b 28 2f a3 da d4 e4 f a9 27 53 4 1b fc ac e6 d 7a 7 ae 63 c5 db e2 ea 94 8b c4 d5 9d f8 90 6b e b1 d d6 eb c6 e cf ad 8 4e d7 e3 5d 50 1e b3 f 5b 23 38 34 68 46 3 8c dd 9c 7d a0 cd 1a 41 1c
步骤三:S盒字节变换和逆S盒字节变换:
//S盒字节变换 uint8_t byteTransformation(uint8_t a, uint8_t x) { uint8_t tmp[8]={0}; for(uint8_t i=0;i<8;i++) { tmp[i]= (((a>>i)&0x1)^((a>>((i+4)%8))&0x1)^((a>>((i+5)%8))&0x1)^((a>>((i+6)%8))&0x1)^((a>>((i+7)%8))&0x1)^((x>>i)&0x1)) << i; } tmp[0] = tmp[0]+tmp[1]+tmp[2]+tmp[3]+tmp[4]+tmp[5]+tmp[6]+tmp[7]; return tmp[0]; } //逆S盒字节变换 uint8_t invByteTransformation(uint8_t a, uint8_t x) { uint8_t tmp[8]={0}; for(uint8_t i=0;i<8;i++) { tmp[i]= (((a>>((i+2)%8))&0x1)^((a>>((i+5)%8))&0x1)^((a>>((i+7)%8))&0x1)^((x>>i)&0x1)) << i; } tmp[0] = tmp[0]+tmp[1]+tmp[2]+tmp[3]+tmp[4]+tmp[5]+tmp[6]+tmp[7]; return tmp[0]; }
S盒变换代码:
//S盒产生 void s_box_gen(void) { uint8_t i,j; uint8_t s_box_ary[16][16] = {0}; //初始化S盒 for(i=0;i<0x10;i++) { for(j=0;j<0x10;j++) { s_box_ary[i][j] = ((i<<4)&0xF0) + (j&(0xF)); } } printf(" 0 1 2 3 4 5 6 7 8 9 A B C D E F"); for(i=0;i<0x10;i++) { printf(" %2x",i); for(j=0;j<0x10;j++) { printf(" %2x",s_box_ary[i][j]); } } //求在GF(2^8)域上的逆,0映射到自身 printf(" "); for(i=0;i<0x10;i++) { for(j=0;j<0x10;j++) { if(s_box_ary[i][j] != 0) { s_box_ary[i][j] = extEuclidPolynomial(s_box_ary[i][j],0x11B); } } } printf(" 0 1 2 3 4 5 6 7 8 9 A B C D E F"); for(i=0;i<0x10;i++) { printf(" %2x",i); for(j=0;j<0x10;j++) { printf(" %2x",s_box_ary[i][j]); } } //对每个字节做变换 for(i=0;i<0x10;i++) { for(j=0;j<0x10;j++) { s_box_ary[i][j]=byteTransformation(s_box_ary[i][j], 0x63); } } printf(" 0 1 2 3 4 5 6 7 8 9 A B C D E F"); for(i=0;i<0x10;i++) { printf(" %2x",i); for(j=0;j<0x10;j++) { printf(" %2x",s_box_ary[i][j]); } } }
输出如下:
0 1 2 3 4 5 6 7 8 9 A B C D E F 0 0 1 2 3 4 5 6 7 8 9 a b c d e f 1 10 11 12 13 14 15 16 17 18 19 1a 1b 1c 1d 1e 1f 2 20 21 22 23 24 25 26 27 28 29 2a 2b 2c 2d 2e 2f 3 30 31 32 33 34 35 36 37 38 39 3a 3b 3c 3d 3e 3f 4 40 41 42 43 44 45 46 47 48 49 4a 4b 4c 4d 4e 4f 5 50 51 52 53 54 55 56 57 58 59 5a 5b 5c 5d 5e 5f 6 60 61 62 63 64 65 66 67 68 69 6a 6b 6c 6d 6e 6f 7 70 71 72 73 74 75 76 77 78 79 7a 7b 7c 7d 7e 7f 8 80 81 82 83 84 85 86 87 88 89 8a 8b 8c 8d 8e 8f 9 90 91 92 93 94 95 96 97 98 99 9a 9b 9c 9d 9e 9f a a0 a1 a2 a3 a4 a5 a6 a7 a8 a9 aa ab ac ad ae af b b0 b1 b2 b3 b4 b5 b6 b7 b8 b9 ba bb bc bd be bf c c0 c1 c2 c3 c4 c5 c6 c7 c8 c9 ca cb cc cd ce cf d d0 d1 d2 d3 d4 d5 d6 d7 d8 d9 da db dc dd de df e e0 e1 e2 e3 e4 e5 e6 e7 e8 e9 ea eb ec ed ee ef f f0 f1 f2 f3 f4 f5 f6 f7 f8 f9 fa fb fc fd fe ff 0 1 2 3 4 5 6 7 8 9 A B C D E F 0 0 1 8d f6 cb 52 7b d1 e8 4f 29 c0 b0 e1 e5 c7 1 74 b4 aa 4b 99 2b 60 5f 58 3f fd cc ff 40 ee b2 2 3a 6e 5a f1 55 4d a8 c9 c1 a 98 15 30 44 a2 c2 3 2c 45 92 6c f3 39 66 42 f2 35 20 6f 77 bb 59 19 4 1d fe 37 67 2d 31 f5 69 a7 64 ab 13 54 25 e9 9 5 ed 5c 5 ca 4c 24 87 bf 18 3e 22 f0 51 ec 61 17 6 16 5e af d3 49 a6 36 43 f4 47 91 df 33 93 21 3b 7 79 b7 97 85 10 b5 ba 3c b6 70 d0 6 a1 fa 81 82 8 83 7e 7f 80 96 73 be 56 9b 9e 95 d9 f7 2 b9 a4 9 de 6a 32 6d d8 8a 84 72 2a 14 9f 88 f9 dc 89 9a a fb 7c 2e c3 8f b8 65 48 26 c8 12 4a ce e7 d2 62 b c e0 1f ef 11 75 78 71 a5 8e 76 3d bd bc 86 57 c b 28 2f a3 da d4 e4 f a9 27 53 4 1b fc ac e6 d 7a 7 ae 63 c5 db e2 ea 94 8b c4 d5 9d f8 90 6b e b1 d d6 eb c6 e cf ad 8 4e d7 e3 5d 50 1e b3 f 5b 23 38 34 68 46 3 8c dd 9c 7d a0 cd 1a 41 1c 0 1 2 3 4 5 6 7 8 9 A B C D E F 0 63 7c 77 7b f2 6b 6f c5 30 1 67 2b fe d7 ab 76 1 ca 82 c9 7d fa 59 47 f0 ad d4 a2 af 9c a4 72 c0 2 b7 fd 93 26 36 3f f7 cc 34 a5 e5 f1 71 d8 31 15 3 4 c7 23 c3 18 96 5 9a 7 12 80 e2 eb 27 b2 75 4 9 83 2c 1a 1b 6e 5a a0 52 3b d6 b3 29 e3 2f 84 5 53 d1 0 ed 20 fc b1 5b 6a cb be 39 4a 4c 58 cf 6 d0 ef aa fb 43 4d 33 85 45 f9 2 7f 50 3c 9f a8 7 51 a3 40 8f 92 9d 38 f5 bc b6 da 21 10 ff f3 d2 8 cd c 13 ec 5f 97 44 17 c4 a7 7e 3d 64 5d 19 73 9 60 81 4f dc 22 2a 90 88 46 ee b8 14 de 5e b db a e0 32 3a a 49 6 24 5c c2 d3 ac 62 91 95 e4 79 b e7 c8 37 6d 8d d5 4e a9 6c 56 f4 ea 65 7a ae 8 c ba 78 25 2e 1c a6 b4 c6 e8 dd 74 1f 4b bd 8b 8a d 70 3e b5 66 48 3 f6 e 61 35 57 b9 86 c1 1d 9e e e1 f8 98 11 69 d9 8e 94 9b 1e 87 e9 ce 55 28 df f 8c a1 89 d bf e6 42 68 41 99 2d f b0 54 bb 16
逆S盒变换代码:
//逆S盒产生 void inv_s_box_gen(void) { uint8_t i,j; uint8_t s_box_ary[16][16] = {0}; uint8_t b=0, bb=0; //初始化S盒 for(i=0;i<0x10;i++) { for(j=0;j<0x10;j++) { s_box_ary[i][j] = ((i<<4)&0xF0) + (j&(0xF)); } } printf(" 0 1 2 3 4 5 6 7 8 9 A B C D E F"); for(i=0;i<0x10;i++) { printf(" %2x",i); for(j=0;j<0x10;j++) { printf(" %2x",s_box_ary[i][j]); } } //对每个字节做变换 for(i=0;i<0x10;i++) { for(j=0;j<0x10;j++) { s_box_ary[i][j]=invByteTransformation(s_box_ary[i][j], 0x05); } } printf(" 0 1 2 3 4 5 6 7 8 9 A B C D E F"); for(i=0;i<0x10;i++) { printf(" %2x",i); for(j=0;j<0x10;j++) { printf(" %2x",s_box_ary[i][j]); } } //求在GF(2^8)域上的逆,0映射到自身 printf(" "); for(i=0;i<0x10;i++) { for(j=0;j<0x10;j++) { if(s_box_ary[i][j] != 0) { s_box_ary[i][j] = extEuclidPolynomial(s_box_ary[i][j],0x11B); } } } printf(" 0 1 2 3 4 5 6 7 8 9 A B C D E F"); for(i=0;i<0x10;i++) { printf(" %2x",i); for(j=0;j<0x10;j++) { printf(" %2x",s_box_ary[i][j]); } } }
输出如下:
0 1 2 3 4 5 6 7 8 9 A B C D E F 0 0 1 2 3 4 5 6 7 8 9 a b c d e f 1 10 11 12 13 14 15 16 17 18 19 1a 1b 1c 1d 1e 1f 2 20 21 22 23 24 25 26 27 28 29 2a 2b 2c 2d 2e 2f 3 30 31 32 33 34 35 36 37 38 39 3a 3b 3c 3d 3e 3f 4 40 41 42 43 44 45 46 47 48 49 4a 4b 4c 4d 4e 4f 5 50 51 52 53 54 55 56 57 58 59 5a 5b 5c 5d 5e 5f 6 60 61 62 63 64 65 66 67 68 69 6a 6b 6c 6d 6e 6f 7 70 71 72 73 74 75 76 77 78 79 7a 7b 7c 7d 7e 7f 8 80 81 82 83 84 85 86 87 88 89 8a 8b 8c 8d 8e 8f 9 90 91 92 93 94 95 96 97 98 99 9a 9b 9c 9d 9e 9f a a0 a1 a2 a3 a4 a5 a6 a7 a8 a9 aa ab ac ad ae af b b0 b1 b2 b3 b4 b5 b6 b7 b8 b9 ba bb bc bd be bf c c0 c1 c2 c3 c4 c5 c6 c7 c8 c9 ca cb cc cd ce cf d d0 d1 d2 d3 d4 d5 d6 d7 d8 d9 da db dc dd de df e e0 e1 e2 e3 e4 e5 e6 e7 e8 e9 ea eb ec ed ee ef f f0 f1 f2 f3 f4 f5 f6 f7 f8 f9 fa fb fc fd fe ff 0 1 2 3 4 5 6 7 8 9 A B C D E F 0 5 4f 91 db 2c 66 b8 f2 57 1d c3 89 7e 34 ea a0 1 a1 eb 35 7f 88 c2 1c 56 f3 b9 67 2d da 90 4e 4 2 4c 6 d8 92 65 2f f1 bb 1e 54 8a c0 37 7d a3 e9 3 e8 a2 7c 36 c1 8b 55 1f ba f0 2e 64 93 d9 7 4d 4 97 dd 3 49 be f4 2a 60 c5 8f 51 1b ec a6 78 32 5 33 79 a7 ed 1a 50 8e c4 61 2b f5 bf 48 2 dc 96 6 de 94 4a 0 f7 bd 63 29 8c c6 18 52 a5 ef 31 7b 7 7a 30 ee a4 53 19 c7 8d 28 62 bc f6 1 4b 95 df 8 20 6a b4 fe 9 43 9d d7 72 38 e6 ac 5b 11 cf 85 9 84 ce 10 5a ad e7 39 73 d6 9c 42 8 ff b5 6b 21 a 69 23 fd b7 40 a d4 9e 3b 71 af e5 12 58 86 cc b cd 87 59 13 e4 ae 70 3a 9f d5 b 41 b6 fc 22 68 c b2 f8 26 6c 9b d1 f 45 e0 aa 74 3e c9 83 5d 17 d 16 5c 82 c8 3f 75 ab e1 44 e d0 9a 6d 27 f9 b3 e fb b1 6f 25 d2 98 46 c a9 e3 3d 77 80 ca 14 5e f 5f 15 cb 81 76 3c e2 a8 d 47 99 d3 24 6e b0 fa 0 1 2 3 4 5 6 7 8 9 A B C D E F 0 52 9 6a d5 30 36 a5 38 bf 40 a3 9e 81 f3 d7 fb 1 7c e3 39 82 9b 2f ff 87 34 8e 43 44 c4 de e9 cb 2 54 7b 94 32 a6 c2 23 3d ee 4c 95 b 42 fa c3 4e 3 8 2e a1 66 28 d9 24 b2 76 5b a2 49 6d 8b d1 25 4 72 f8 f6 64 86 68 98 16 d4 a4 5c cc 5d 65 b6 92 5 6c 70 48 50 fd ed b9 da 5e 15 46 57 a7 8d 9d 84 6 90 d8 ab 0 8c bc d3 a f7 e4 58 5 b8 b3 45 6 7 d0 2c 1e 8f ca 3f f 2 c1 af bd 3 1 13 8a 6b 8 3a 91 11 41 4f 67 dc ea 97 f2 cf ce f0 b4 e6 73 9 96 ac 74 22 e7 ad 35 85 e2 f9 37 e8 1c 75 df 6e a 47 f1 1a 71 1d 29 c5 89 6f b7 62 e aa 18 be 1b b fc 56 3e 4b c6 d2 79 20 9a db c0 fe 78 cd 5a f4 c 1f dd a8 33 88 7 c7 31 b1 12 10 59 27 80 ec 5f d 60 51 7f a9 19 b5 4a d 2d e5 7a 9f 93 c9 9c ef e a0 e0 3b 4d ae 2a f5 b0 c8 eb bb 3c 83 53 99 61 f 17 2b 4 7e ba 77 d6 26 e1 69 14 63 55 21 c 7d
以上代码肯定不是最优代码,欢迎拍砖,并在留言区留下您宝贵意见,谢谢!
以上是关于AES-128加密过程中的S盒构造的主要内容,如果未能解决你的问题,请参考以下文章
AES-128-CBC加密过程中,我想随机产生16位的向量,希望各位能给我一下C语言代码的实现。
AES128_CBC_NoPading加密、sha256withRSA签名