UVA297：Quadtrees（四分树）

Posted 2020-12-24 alphawa

题目描述

四象树是每个内结点均有4个子结点的特殊四叉树，它可用于描述平面上黑白图像。平面上的黑白图像是32行×32列的正方形，每个格子称为1个象素，是最小的图像单位。正方形图像可分成四个相等的小正方形，可按直角坐标系四个象限的顺序分别编号1，2，3，4，分别对应于四象树的四个子结点。这样，32行×32列的图像就对应于一棵深度为6的完全四叉树，最底层的每个叶结点正好对应于一个象素。但我们可以压缩四象树的结点数量。

当图像上某个区域为全白或者全黑时，可把该区域在四象树上对应的结点描述为全白(用小写字母e表示)或者全黑（用小写字母f表示），并且对这样的结点不再扩展子结点，因为再扩展出的子树上每个结点都是相同的颜色。

只有当图像上某个区域为“杂色”时，才继续划分成四个子区域（在四象树上对应的结点用小写字母p表示），然后“纯”色的子区域也不再扩展，并继续扩展“杂”色子区域。例如，下图左、中两个图像可分别用它们下边的四象树描述。

 

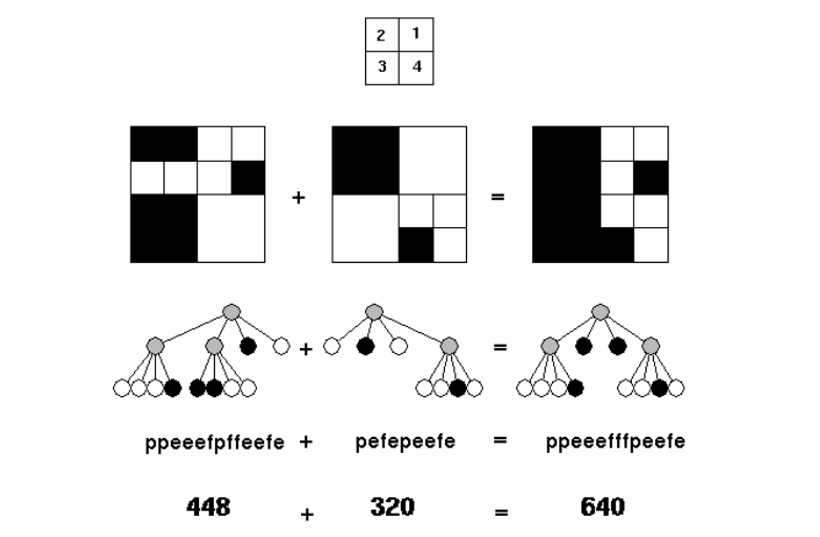
我们感兴趣的问题是：当两个大小均为32*32的黑白图像叠加后，合成的新图像是什么样子。合成的规则是：当一个图像上某个区域为全黑时，新图像的这个区域即为全黑；当一个图像上某个区域为全白时，新图像的这个区域的颜色是另加一个图像上这个区域的颜色。上图准确地示例了本合成的规则。

我们给出两个图像对应四象树的先序遍历顺序，求合成后的图像中，黑色象素点的数量。

输入

 多组测试数据，第1行一个整数T，表示测试数据的组数，每组数据的格式为：

第1行：一个字符串，描述第1棵四象树的先序序列

第2行：一个字符串，描述第2棵四旬树的先序序列

输出

 对每组数据，在单独一行上输出一个整数，表示合成后的图像上黑色象素的数量，格式如输出样例所示：

样例输入

3
ppeeefpffeefe
pefepeefe
peeef
peefe
peeef
peepefefe

样例输出

There are 640 black pixels.
There are 512 black pixels.
There are 384 black pixels.

 我直接把BZOJ的翻译粘过来了（逃

思路1：数据量很小。我第一次写时直接模拟了两棵四叉树的建树与搜索，然后捎带着把最后的黑色个数算出来了。其中黑色结点的值跟它的深度有关，写一写就能找到规律。

 1 #include <cstdio>
 2 #include <cstring>
 3 #include <iostream>
 4 #include <cmath>
 5 using namespace std;
 6 
 7 struct node
 8 {
 9     char c;
10     node *ptr[4];
11     node(){for (int i = 0; i < 4; i++)    ptr[i] = NULL;}
12 };
13 
14 node *root1, *root2;
15 
16 int sum, cnt;//sum是最终结果，cnt是记录字符串走到哪个位置了
17 
18 void release(node *root)//释放
19 {
20     if (!root)    return;
21     for (int i = 0; i < 4; i++)
22         release(root->ptr[i]);
23     delete root;
24 }
25 
26 void build(string cur, node *&root)//建树，记得root要加地址符
27 {
28     root = new node();
29     root->c = cur[cnt++];
30     if (root->c == ‘p‘)
31         for (int i = 0; i < 4; ++i)
32         {
33             root->ptr[i] = new node();
34             build(cur, root->ptr[i]);
35         }
36 }
37 
38 void dfs(node *root1, node *root2, int depth)
39 {
40     //大概分了三种情况讨论
41     if (root1->c == ‘f‘ || root2->c == ‘f‘)//有一个是黑
42     {
43         sum += pow(4,6-depth);//数学可推……
44         return;
45     }
46     else if (root1->c == ‘e‘ && root2->c == ‘e‘)//全是白
47         return;
48     //对于‘p‘的点深搜
49     bool flag1 = root1->c==‘p‘, flag2 = root2->c==‘p‘;
50     node *x = root1, *y = root2;
51     for (int i = 0; i < 4; i++)
52     {
53         if (flag1)    x = root1->ptr[i];
54         if (flag2)    y = root2->ptr[i];
55         dfs(x, y, depth+1);
56     }
57 }
58 
59 int main()
60 {
61     int test;
62     scanf("%d", &test);
63 
64     while (test--)
65     {
66         sum = 0;
67         string s,t;
68         cin >> s >> t;
69         cnt = 0, build(s, root1);
70         cnt = 0, build(t, root2);
71 
72         dfs(root1, root2, 1);
73 
74         printf("There are %d black pixels.
", sum);
75 
76         release(root1),release(root2);
77     }
78 
79     return 0;
80 }

 

思路2：书上代码思路是在32*32的正方形里面涂色然后查找，貌似跟树也没什么关系了……书中的注释已经很明白了，见代码。（PS：UVA有毒）

 1 #include <cstdio>
 2 #include <cstring>
 3 
 4 const int len = 32;
 5 const int maxn = 1024 + 10;
 6 //下面这个char数组和int变量定义顺序变一下UVA居然会WA啊！
 7 //我从未见过如此厚颜无耻之OJ
 8 char s[maxn];
 9 int buf[len][len], cnt;
10 
11 //把字符串s[p..]导出到以（r，c）为左上角，边长为w的缓冲区中
12 //2 1
13 //3 4
14 void draw(const char* s, int& p, int r, int c, int w)
15 {
16     char ch = s[p++];
17     if (ch == ‘p‘)
18     {
19         draw(s, p, r    , c+w/2, w/2);//1
20         draw(s, p, r    , c    , w/2);//2
21         draw(s, p, r+w/2, c    , w/2);//3
22         draw(s, p, r+w/2, c+w/2, w/2);//4
23     }
24     else if (ch == ‘f‘)
25         for (int i = r; i < r+w; i++)
26             for (int j = c; j < c+w; j++)
27                 if (buf[i][j] == 0)
28                     buf[i][j] = 1,cnt++;
29 }
30 
31 int main()
32 {
33     int t;
34     scanf("%d", &t);
35 
36     while (t--)
37     {
38         memset(buf, 0, sizeof(buf));
39         cnt = 0;
40         for (int i = 0; i < 2; i++)
41         {
42             scanf("%s",s);
43             int p = 0;
44             draw(s, p, 0, 0, len);
45         }
46                     
47         printf("There are %d black pixels.
", cnt);
48 
49     }
50 
51     return 0;
52 }