JPEG格式压缩算法

Posted 2020-12-24 torrance

• 一、JPEG原理概述
• 二、JPEG原理详细分析及压缩算法过程
  • 1、Color Model Conversion (色彩模型)
  • 2、DCT (Discrete Cosine Transform 离散余弦变换)
  • 3、数据量化
  • 4、重排列 DCT 结果
  • 5、基于差分脉冲编码调制的DC编码
  • 6、RLE编码
  • 7、范式Huffman编码
  • 8、JPEG压缩过程总结
• 三、JPEG存储格式
• 四、JPEG压缩的GPU优化

一、JPEG原理概述

JPEG 是 Joint Photographic Experts Group 的缩写，即 ISO 和 IEC 联合图像专家组，负责静态图像压缩标准的制定，这个专家组开发的算法就被称为 JPEG 算法，并且已经成为了大家通用的标准，即 JPEG 标准。 JPEG 压缩是有损压缩，但这个损失的部分是人的视觉不容易察觉到的部分，它充分利用了人眼对计算机色彩中的高频信息部分不敏感的特点，来大大节省了需要处理的数据信息。

JPEG格式在图片中的地位相当于mp3格式在音乐中的地位一样，都是对于原始数据的有损压缩，举个例子，一张1000*1000的图片，RGB三个通道各占一个字节，所以未经压缩的情况下其图像信息的大小大约为1000*1000*3=3000000字节，约等于2.86MB，这个文件大小看过小说的人都能想象到，大概应该是150w字到200w字，而经过JPEG压缩后，其大小能达到300KB左右，压缩比一般为1:8左右。而JPEG如何实现如此高的压缩比呢？前面提到过JPEG是有损压缩，所谓有损，就是把图片中不重要，人眼对其不敏感的东西过滤掉，以达到压缩文件大小的目的，比如12345.0000000001这个数字，我们可以将其视为12345，而忽略的部分就是因为其包含的信息太少。接下来，在存储过程中，我们可以使用一些特殊的方式对存储结构进行优化，以达到进一步压缩文件大小的目的。所以，对原始图像信息进行JPEG编码的过程就分为两大步：第一步，去除视觉上的多余信息，即空间冗余度；第二步，去除数据本身的多余信息，即结构冗余度。

二、JPEG原理详细分析及压缩算法过程

整个JPEG编码中主要涉及的内容包括：Color Model Conversion (色彩模型)、DCT (Discrete Cosine Transform 离散余弦变换)、数据量化、重排列 DCT 结果、基于差分脉冲编码调制的DC编码、RLE编码和范式Huffman编码。接下来我们详细讲解一下。

1、Color Model Conversion (色彩模型)

在图像处理中，为了利用人的视角特性，从而降低数据量，通常把 RGB 空间表示的彩色图像变换到其他色彩空间。现在我们采用的色彩空间变换有三种：YIQ，YUV 和 YCrCb。

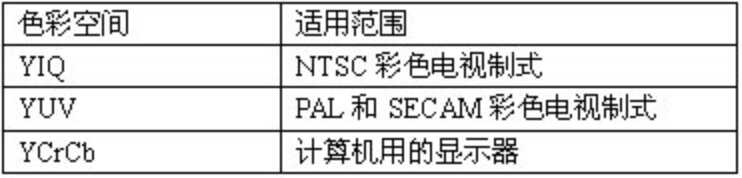
对计算机而言，计算机用的数字域的色彩空间变换与电视模拟域的色彩空间变换不同，它们的分量使用 Y、Cr 和 Cb 来表示，所以需要将RGB转化为YCrCb，其转换关系如下： 

这里的Y表示亮度(Luminance)，Cb和Cr分别表示绿色和红色的“色差值”。

从这里，就可以看出，计算出来的 Y、Cr 和 Cb 分量，会出现大量的小数，即浮点数，从而导致了在JPEG 编码过程中会出现大量的浮点数的运算，当然经过一定的优化，这些浮点数运算可以用移位与加法这些计算机能更快速处理的方式来对其进行编码。

注意一点，实际上，JPEG 算法与色彩空间无关，色彩空间是涉及到图像采样的问题，它和数据的压缩并没有直接的关系。JPEG 算法处理的彩色图像是单独的彩色分量图像，因此它可以压缩来自不同色彩空间的数据，如 RGB，YcbCr 和 CMYK。

人眼对构成图像的不同频率成分具有不同的敏感度，这个是由人眼的视觉生理特性所决定的。如人的眼睛含有对亮度敏感的柱状细胞1.8亿个，含有对色彩敏感的椎状细胞0.08亿个，由于柱状细胞的数量远大于椎状细胞，所以眼睛对亮度的敏感程度要大于对色彩的敏感程度。比如下面这张图：

可以明显看到，亮度图的细节更加丰富。JPEG把图像转换为YCbCr之后，就可以针对数据得重要程度的不同做不同的处理。这就是为什么JPEG一般使用这种颜色空间的原因。

2、DCT (Discrete Cosine Transform 离散余弦变换)

前面我们提到过，人眼对计算机色彩中的高频信息部分不敏感，所以如果能将图像中的高频部分过滤掉就可以实现对图像的压缩了。问题是，我们如何将色彩域的图像转换到频域上呢？在数字通信原理中接触到过快速傅立叶变换，离散余弦变换就是傅立叶变换的另外一种形式，傅立叶变换可以将时域信号转化成频域信号，其源于傅立叶曾经提出的一个著名想法，他认为任何周期性的函数，都可以分解为一系列的三角函数的组合，这个想法当时被拉格朗日所质疑，他提出三角函数无论如何组合，都无法表达带有“尖角”的函数，虽然最后拉格朗日是正确的，但是只要三角函数足够多，我们就可以无限逼近最终结果，举个例子，来看一下如何用三角函数描述一个矩形方波：

 

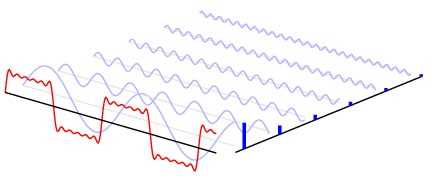
当我们要处理的不再是函数，而是一堆离散的数据时，那么傅里叶变化出来的函数只含有余弦项，这种变换称为离散余弦变换。举个例子，有一组一维数据[x0,x1,x2,…,xn-1],那么可以通过DCT变换得到n个变换级数Fi：

此时原始数据Xi可以通过离散余弦变换变化的逆变换（IDCT)表达出来：

也就是说，经过DCT变换，可以把一个数组分解成数个数组的和，如果我们数组视为一个一维矩阵，那么可以把结果看做是一系列矩阵的和：

举个例子，我们有一个长度为8的数字，为50，55，67，80，-10，-5，20，30，经过DCT转换，得到8个级数为287.0，106.3，14.2，-110.8，9.2，65.7，-8.2，-43.9，根据公式把这个数组转换为8个新的数组的和，如果我们使用图像来表达的话，就可以发现DCT转换的有趣之处了：

 

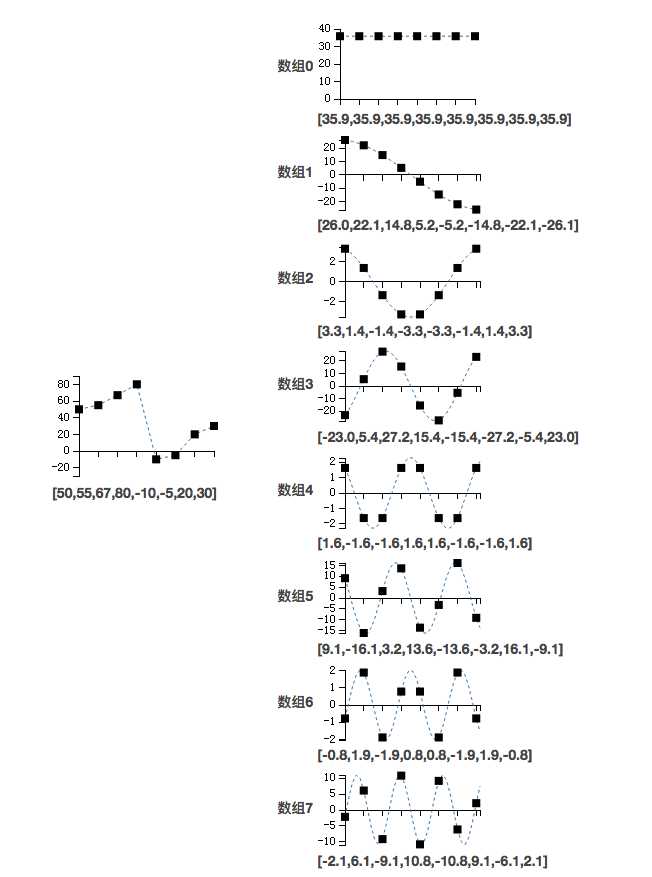
从上图可以看出，看似杂乱的数据经过DCT变换之后会变成几个工整变化的数据，而DCT转换后的数组中第一个是直线数据，所以称之为直流数据，简称DC，其余数据为交流数据，简称AC。

在JPEG压缩算法中，先会把整个图像分割成8*8的图像块，再对每一个图像块进行DCT变换，而为的DCT变换公式为：

我们来用一个极端的例子看一下DCT变换的威力究竟有多大：

经过DCT变换之后，整个图像的能量都被集中在了左上角的直流分量中。再来看一个普遍一点的例子：

可以明显看出，DCT变化后，矩阵被分成了直流分量和交流分量两个部分，而一直到这里，整个过程都是可逆的，图像仍然是无损的，而这一步为后面的图像压缩起了铺垫作用，所以DCT变换是JPEG压缩算法的核心。

3、数据量化

经过前两步之后，整个图像会分解成若干个8*8的小矩阵，而每个小矩阵又分为Y、Cb、Cr三个分量，我们以一个Y分量矩阵为例：

现在的问题在于如何在可以损失一些精度的情况下用更少的空间存储这些浮点数呢？答案就是量子化。举个例子，比如在游戏中处理角色的面朝方向时，一般不用0到2π这样的浮点数，而是把方向分成16个区间，用整数来表示，这样一个方向只需要4个bit。JPEG提供的量子化算法如下：

其中G是我们要处理的图像矩阵，Q是量化系数矩阵，在JPEG算法中提供了两张标准量化系数矩阵，分别用于处理亮度数据和色差数据：

经过量子化后，原矩阵变为了：

我们可以看到，经过压缩之后出现了大面积的0，这十分有利于数据的压缩，在实际的压缩过程中，我们还可以将这个矩阵乘以一个系数，代表压缩率，以控制出现更多或更少的0，进而控制压缩质量，系数的取值是0到1之间的实数。总体上来说，DCT 变换实际是空间域的低通滤波器。对亮度分量采用细量化，对色差分量采用粗量化。

4、重排列 DCT 结果

在量化之后，8*8的矩阵仍然是二维矩阵，如何调整我们DCT的结果能更高地提升压缩率呢？观察量化后的矩阵，我们发现大量信息都集中在左上角，所以我们采用ZigZag编排，如图：

其结果就变为了：?26，?3，0，?3，?3，?6，2，?4，1 ?4，1，1，5，1，2，?1，1，?1，2，0，0，0，0，0，?1，?1，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0。增加了连续0的个数，这样我们就可以更好地进行数据压缩。

5、基于差分脉冲编码调制的DC编码

观察8*8矩阵DCT之后的DC分量和AC分量，我们可以看出，DC分量的值很明显大于AC分量，而且对于相邻的8*8矩阵，其DC分量的系数值变化不大，这是因为图片的能量基本都集中在低频分量中，而图片大部分是有连续性的，即相邻矩阵中能量变化比较平稳，所以我们采用差分脉冲调制编码（DPCM）技术，对相邻图像块之间量化DC系数的差值进行编码。

6、RLE编码

Run Length Encoding，行程编码又称“运行长度编码”或“游程编码”，它是一种无损压缩编码。例如：5555557777733322221111111，这个数据的一个特点是相同的内容会重复出现很多次，那么就可以用一种简化的方法来记录这一串数字，如（5，6）（7，5）（3，3）（2，4）（1，7）即为它的行程编码。行程编码的位数会远远少于原始字符串的位数。举个例子来看一下：57，45，0，0，0，0，23，0，-30，-16，0，0，1，0，0，0，0 ，0 ，0 ，0，..，0，可以表示为：(0，57) ; (0，45) ; (4，23) ; (1，-30) ; (0，-16) ; (2，1) ; EOB。即每组数字的头一个表示0的个数，而且为了能更有利于后续的处理，必须是 4 bit，就是说，只能是 0~15，这是这个行程编码的一个特点。JPEG使用了1个字节的高4位来表示连续“0”的个数，而使用它的低4位来表示编码下一个非“0”系数所需要的位数，跟在它后面的是量化AC系数的数值。其中（0，0）和（15，0）比较特殊，（0，0）代表块结束，（15，0）代表已经有16个连续的0。

7、范式Huffman编码

DPCM和RLE编码后，为了进一步压缩，我们采用范式Huffman编码，用一个例子来看一下ZIGZAG后的数据是如何压缩的：

由于第一个是DC分量，采用DPCM技术，所以我们假设他的上一个矩阵的DC分量值为0，即35代表了其差值，则我们对原始数据的AC分量进行RLE编码后结果为：

接下来我们要处理的是括号右边的数据，JPEG提供了一张标准的码表：

所以我们的原始数据变成了：

将括号内的前两个字进行合并，变成一个字节：

接下来我们就要使用哈夫曼编码了，假设我们现在的Huffman表如下，DC分量：

AC分量： 

 

经过哈夫曼编码后，数据变为了：

综上，最终我们使用了10个字节的空间保存了原本64字节的数据，至此，整个JPEG压缩算法全部结束。

8、JPEG压缩过程总结

所以，我们最后总结一下整个JPEG压缩图片的过程：

• 将整张图片分为若干8*8的矩阵
• 对每个8*8矩阵进行DCT变换
• 对DCT后的矩阵进行量子化
• 重新进行ZIGZAG排序
• 将DC分量和AC分量分别进行DPCM和RLE编码
• 将整体信息进行Huffman编码

三、JPEG存储格式

要注意的是，前面我们讲的都是JPEG压缩算法，这个标准只说明了如果将图片压缩成字节流以及重新解码成图片的过程，而JPEG标准定义的文件存储格式是JIF，但是其有一定缺陷，使用率不高，而后陆续又出现了不同的文件存储格式，如JFIF、EXIF等，但是他们都遵循JIF。

前面讲了整个JPEG压缩算法的全过程，显然，JPEG大体的存储格式就基本清晰了，我们至少需要字段去存储量化表、哈夫曼表和压缩后的数据。接下来我们就看一下JPEG格式的存储格式到底是什么样的：

JPEG以0xFF为Marker，当遇到0xFF就需要判断：

• 如果是0X00，表示0XFF是图像流的组成部分；需要进行译码；
• 如果是0XD0～0XD7，组成RSTn标记，需要忽视整个RSTn标记，即不对当前0XFF和紧接着的0XDn两个字节进行译码，并按RST标记的规则调整译码变量；
• 如果是0XFF，忽略当前0XFF，对后一个0XFF进行判断；
• 如果是已有的头部标记，则进行对应的译码；
• 如果是其它数值，忽然当前0XFF，并保留紧接着此数值用于译码；

而头部标记码及其含义如下：

SOI，Start Of Image， 图像开始，标记代码为固定值0XFFD8，用2字节表示；

APP0，Application 0, 应用程序保留标记0，标记代码为固定值0XFFE0，用2字节表示；该标记码之后包含了9个具体的字段：

（1）数据长度：2个字节，用来表示（1）--（9）的9个字段的总长度，即不包含标记代码但包含本字段；

（2）标示符：5个字节，固定值0X4A6494600，表示了字符串“JFIF0”；

（3）版本号：2个字节，一般为0X0102，表示JFIF的版本号为1.2；但也可能为其它数值，从而代表了其它版本号；

（4）X,Y方向的密度单位：1个字节，只有三个值可选，0：无单位；1：点数每英寸；2：点数每厘米；

（5）X方向像素密度：2个字节，取值范围未知；

（6）Y方向像素密度：2个字节，取值范围未知；

（7）缩略图水平像素数目：1个字节，取值范围未知；

（8）缩略图垂直像素数目：1个字节，取值范围未知；

（9）缩略图RGB位图：长度可能是3的倍数，保存了一个24位的RGB位图；如果没有缩略位图（这种情况更常见），则字段（7）（8）的取值均为0；

APPn, Application n, 应用程序保留标记n(n=1---15),标记代码为2个字节，取值为0XFFE1--0XFFEF；包含了两个字段：

（1）数据长度，2个字节，表示（1）（2）两个字段的总长度；即，不包含标记代码，但包含本字段；

（2）详细信息：数据长度-2个字节，内容不定；

DQT，Define Quantization Table, 定义量化表；标记代码为固定值0XFFDB；包含9个具体字段：

（1）数据长度：2个字节，表示（1）和多个（2）字段的总长度；即，不包含标记代码，但包含本字段；

（2）量化表：数据长度-2个字节，其中包括以下内容：

（a）精度及量化表ID，1个字节，高4位表示精度，只有两个可选值，0：8位；1:16位；低4位表示量化表ID，取值范围为0--3；

（b）表项，64*（精度取值+1）个字节，例如，8位精度的量化表，其表项长度为64*（0+1）=64字节；

本标记段中，（2）可以重复出现，表示多个量化表，但最多只能出现4次；

SOFO，Start Of Frame, 帧图像开始，标记代码为固定值0XFFC0；包含9个具体字段：

（1）数据长度：2个字节，（1）--（6）共6个字段的总长度；即，不包含标记代码，但包含本字段；

（2）精度：1个字节，代表每个数据样本的位数；通常是8位；

（3）图像高度：2个字节，表示以像素为单位的图像高度，如果不支持DNL就必须大于0；

（4）图像宽度：2个字节，表示以像素为单位的图像宽度，如果不支持DNL就必须大于0；

（5）颜色分量个数：1个字节，由于JPEG采用YCrCb颜色空间，这里恒定为3；

（6）颜色分量信息：颜色分量个数*3个字节，这里通常为9个字节；并依此表示如下一些信息：

（a）颜色分量ID： 1个字节；

（b）水平/垂直采样因子：1个字节，高4位代表水平采样因子，低4位代表垂直采样因子；

（c）量化表：1个字节，当前分量使用的量化表ID；

本标记段中，字段（6）应该重复出现3次，因为这里有3个颜色分量；

DHT，Define Huffman Table定义Huffman表，标记码为0XFFC4；包含2个字段：

（1）数据长度，2个字节，表示（1）--（2）的总长度，即，不包含标记代码，但包含本字段；

（2）Huffman表，数据长度-2个字节，包含以下字段：

（a）表ID和表类型，1个字节，高4位表示表的类型，取值只有两个；0：DC直流；1：AC交流；低4位，Huffman表ID；需要提醒的是，DC表和AC表分开进行编码；

（b）不同位数的码字数量，16个字节；

（c）编码内容，16个不同位数的码字数量之和（字节）；

本标记段中，字段（2）可以重复出现，一般需要重复4次。

DRI，Define Restart Interval，定义差分编码累计复位的间隔，标记码为固定值0XFFDD；

包含2个具体字段：

（1）数据长度：2个字节，取值为固定值0X0004，表示（1）（2）两个字段的总长度；即，不包含标记代码，但包含本字段；

（2）MCU块的单元中重新开始间隔：2个字节，如果取值为n，就代表每n个MCU块就有一个RSTn标记；第一个标记是RST0，第二个是RST1,RST7之后再从RST0开始重复；如果没有本标记段，或者间隔值为0，就表示不存在重开始间隔和标记RST；

SOS，Start Of Scan，扫描开始；标记码为0XFFDA，包含2个具体字段：

（1）数据长度：2个字节，表示（1）--（4）字段的总长度；

（2）颜色分量数目：1个字节，只有3个可选值，1：灰度图；3：YCrCb或YIQ；4：CMYK；

（3）颜色分量信息：包括以下字段，

（a）颜色分量ID：1个字节；

（b）直流/交流系数表ID，1个字节，高4位表示直流分量的Huffman表的ID；低4位表示交流分量的Huffman表的ID；

（4）压缩图像数据

（a）谱选择开始：1个字节，固定值0X00；

（b）谱选择结束：1个字节，固定值0X3F；

（c）谱选择：1个字节，固定值0X00；

本标记段中，（3）应该重复出现，有多少个颜色分量，就重复出现几次；本段结束之后，就是真正的图像信息了；图像信息直到遇到EOI标记就结束了；

EOI，End Of Image，图像结束；标记代码为0XFFD9；

四、JPEG压缩的GPU优化

CUDA是Nvidia出的面向GPU编程的平台，在CUDA中，将PC称为Host端，显卡称为Device端，提供了__global__宏用来定义核函数进行GPU运算，以及许多malloc、free、memcpy函数用来申请、释放显存，或将数据在内存和显存间传送，用<<<N，M>>>来指定开启N个线程块，每个块内M个线程来执行核函数。

举个例子看一下：

 1 #include <stdio.h>
 2 #include<cuda_runtime.h>
 3  
 4 //__global__声明的函数，告诉编译器这段代码交由CPU调用，由GPU执行
 5 __global__ void add(const int *dev_a,const int *dev_b,int *dev_c)
 6 {
 7     int i=threadIdx.x;
 8     dev_c[i]=dev_a[i]+dev_b[i];
 9 }
10  
11 int main(void)
12 {
13     //申请主机内存，并进行初始化
14     int host_a[512],host_b[512],host_c[512];
15     for(int i=0;i<512;i++)
16     {
17         host_a[i]=i;
18         host_b[i]=i<<1;
19     }
20  
21     //定义cudaError，默认为cudaSuccess(0)
22     cudaError_t err = cudaSuccess;
23  
24     //申请GPU存储空间
25     int *dev_a,*dev_b,*dev_c;
26     err=cudaMalloc((void **)&dev_a, sizeof(int)*512);
27     err=cudaMalloc((void **)&dev_b, sizeof(int)*512);
28     err=cudaMalloc((void **)&dev_c, sizeof(int)*512);
29     if(err!=cudaSuccess)
30     {
31         printf("the cudaMalloc on GPU is failed");
32         return 1;
33     }
34     printf("SUCCESS");
35     //将要计算的数据使用cudaMemcpy传送到GPU
36     cudaMemcpy(dev_a,host_a,sizeof(host_a),cudaMemcpyHostToDevice);
37     cudaMemcpy(dev_b,host_b,sizeof(host_b),cudaMemcpyHostToDevice);
38  
39     //调用核函数在GPU上执行。数据较少，之使用一个Block，含有512个线程
40     add<<<1,512>>>(dev_a,dev_b,dev_c);
41     cudaMemcpy(&host_c,dev_c,sizeof(host_c),cudaMemcpyDeviceToHost);
42     for(int i=0;i<512;i++)
43         printf("host_a[%d] + host_b[%d] = %d + %d = %d
",i,i,host_a[i],host_b[i],host_c[i]);
44     cudaFree(dev_a);//释放GPU内存
45     cudaFree(dev_b);//释放GPU内存
46     cudaFree(dev_c);//释放GPU内存
47     return 0 ;
48 }

所幸的是CUDA已经将GPU的多线程优化封装到了函数中，我们只需要直接调用NPP库内的函数即可。

经过测试，使用GPU优化后其效率是Golang中graphics库的10倍，是resize库的5倍左右。

 

-------------------------------------------------------------------------------------------------------------------------------------

参考资料：

1. https://www.ibm.com/developerworks/cn/linux/l-cn-jpeg/index.html
2. 《GPU高性能编程CUDA实战》

说明：本文参考了众多网络资料整理而成，感谢各位大牛的付出！