平面向量习题

Posted 2020-12-24 wanghai0666

(fbox{例1})

设(vec{a}，vec{b})为单位向量，若向量(vec{c})满足(|vec{c}-(vec{a}+vec{b})|=|vec{a}-vec{b}|)，则向量(|vec{c}|)的最大值为多少？

法1：最容易想到两边平方，整理得到(vec{c}^2-2(vec{a}+vec{b})cdot vec{c}+4vec{a}vec{b}=0)，分解为((vec{c}-2vec{a})(vec{c}-2vec{b})=0)，到此思路受阻。

法2：本题目用到绝对值不等式和均值不等式，由题目得到(|vec{c}-(vec{a}+vec{b})|=|vec{a}-vec{b}|ge |vec{c}|-|vec{a}+vec{b}|)，即(|vec{c}|leq |vec{a}+vec{b}|+|vec{a}-vec{b}|)，接下来需要求(|vec{a}+vec{b}|+|vec{a}-vec{b}|)的最大值。(|vec{a}+vec{b}|+|vec{a}-vec{b}|leq sqrt{2(|vec{a}+vec{b}|)^2+2(|vec{a}-vec{b}|)^2}=sqrt{2(2vec{a}^2+2vec{b}^2)}=2sqrt{2})，当且仅当(|vec{a}+vec{b}|=|vec{a}-vec{b}|)，即(vec{a}perpvec{b})时取到等号，故(|vec{c}|leq 2sqrt{2})。
(fbox{例1+1})
设(vec{a}，vec{b})为单位向量，且(vec{a}perp vec{b})，若向量(vec{c})满足(|vec{c}-(vec{a}+vec{b})|=|vec{a}-vec{b}|)，则向量(|vec{c}|)的最大值为多少？

法1：采用上题的法2.

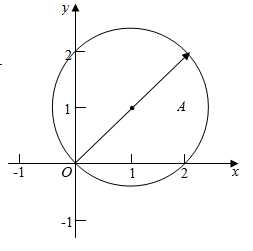
法2：由于(vec{a}，vec{b})为单位向量，且(vec{a}perp vec{b})，故设(vec{a}=(1，0)，vec{b}=(0，1)，vec{c}=(x，y))，由(|vec{c}-(vec{a}+vec{b})|=|vec{a}-vec{b}|)得到，(|(x，y)-(1，1)|=|(1，-1)|)，即(sqrt{(x-1)^2+(y-1)^2}=sqrt{1+1}=sqrt{2})，即((x-1)^2+(y-1)^2=2)，
故(vec{c})的终点坐标对应的轨迹为圆心为((1，1))，半径为(sqrt{2})的圆，又由于圆过圆心，则(|vec{c}|)的最大值为圆的直径(2sqrt{2})。

(fbox{例1+2})
已知(vec{a})，(vec{b})是单位向量，(vec{a}cdot vec{b}=0)，若向量(vec{c})满足(|vec{c}-vec{a}-vec{b}|=1)，则(|vec{c}|)的最大值为()
A.(sqrt{2}-1) (hspace{1cm}) B.(sqrt{2}) (hspace{1cm}) C.(sqrt{2}+1) (hspace{1cm}) D.(sqrt{2}+2)

法1：从形入手，条件(|vec{c}-(vec{a}+vec{b})|=1)可以理解为如图的情况，而(|vec{a}+vec{b}|=sqrt{2})，向量(vec{c})的终点在单位圆上，故向量(|vec{c}|)的最大值为(sqrt{2}+1)，故选C。

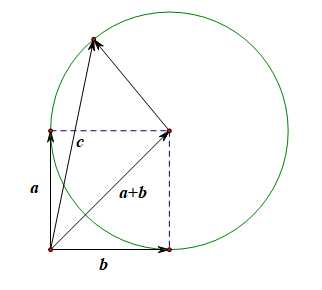
法2：从数的角度，由题意得到(|vec{a}|=|vec{b}|=1，vec{a}cdotvec{b}=0)，所以(|vec{a}+vec{b}|=sqrt{2})，又因为(|vec{c}-vec{a}-vec{b}|=1)，所以(|vec{c}-vec{a}-vec{b}|^2=vec{c}^2-2vec{c}cdot(vec{a}+vec{b})+(vec{a}+vec{b})^2=1)，设(vec{c})与(vec{a}+vec{b})的夹角为( heta)，则(|vec{c}|^2-2|vec{c}| imessqrt{2}cos heta+2=1)，即(|vec{c}|^2+1=2sqrt{2}|vec{c}|cos hetaleq 2sqrt{2}|vec{c}|)，即(|vec{c}|^2-2sqrt{2}|vec{c}|+1leq 0)，解得(sqrt{2}-1leq |vec{c}|leq sqrt{2}+1)。

法3：数形结合，由于(vec{a}，vec{b})为单位向量，且(vec{a}perp vec{b})，故设(vec{a}=(1，0)，vec{b}=(0，1)，vec{c}=(x，y))，则(vec{c}-vec{a}-vec{b}=(x-1，y-1))，由(|vec{c}-(vec{a}+vec{b})|=1)可得，(sqrt{(x-1)^2+(y-1)^2}=1)，即((x-1)^2+(y-1)^2=1)，即向量(vec{c})的终点坐标在圆心位于点((1，1))半径为(1)的圆上，故(|vec{c}|)的最大值是(sqrt{2}+1)，当然也可以知道(|vec{c}|)的最小值是(sqrt{2}-1)。

(fbox{例2})
设(O)在(Delta ABC)内部，且有(overrightarrow{OA}+2overrightarrow{OB}+3overrightarrow{OC}=vec{0})，则(Delta ABC)的面积与(Delta AOC)的面积之比为多少？

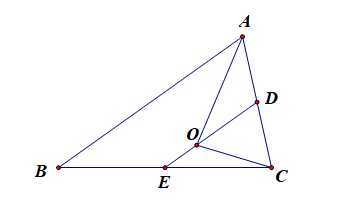
分析：由题目可知((overrightarrow{OA}+overrightarrow{OC})+2(overrightarrow{OB}+overrightarrow{OC})=vec{0})，如图即(2overrightarrow{OD}=-4overrightarrow{OE})，即(overrightarrow{OD}=-2overrightarrow{OE})，故点(O)是中位线(DE)上靠近点(E)的三等分点。令点(B)到边(AC)的高线为(h)，则(S_{Delta ABC}=cfrac{1}{2}cdot ACcdot h)，(S_{Delta AOC}=cfrac{1}{2}cdot ACcdot cfrac{h}{2}cdot cfrac{2}{3}=cfrac{1}{3}cdotcfrac{1}{2}cdot ACcdot h)，故(Delta ABC)的面积与(Delta AOC)的面积之比为3。

(fbox{例3})

设F(_1)、F(_2)为双曲线(cfrac{x^2}{a^2}-cfrac{y^2}{b^2}=1(a>0，b>0))的左右焦点，(P)为双曲线右支上的一点，满足((overrightarrow{OP}+overrightarrow{OF_2})cdot overrightarrow{PF_2}=0)，(O)为坐标原点，且(3|overrightarrow{PF_1}|=4|overrightarrow{PF_2}|)，则双曲线的离心率是多少？

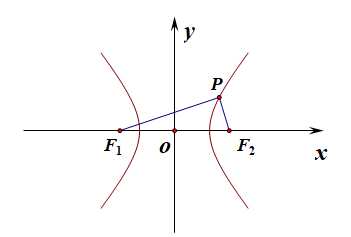
分析：设点(P(x，y))，由点(F_1(-c，0))和点(F_2(c，0))，得到(overrightarrow{OP}=(x，y))，(overrightarrow{OF_2}=(c，0))，(overrightarrow{OP}+overrightarrow{OF_2}=(c+x，y))，(overrightarrow{PF_1}=(-c-x，-y))，(overrightarrow{PF_2}=(c-x，-y))，

由((overrightarrow{OP}+overrightarrow{OF_2})cdot overrightarrow{PF_2}=0)得到，((c-x)(c+x)-y^2=0)，即(c^2=x^2+y^2)，即点(P)在以坐标原点为圆心，以(c)为半径的圆上，故有(overrightarrow{PF_1}cdot overrightarrow{PF_1}=0)，这样(3|overrightarrow{PF_1}|=4|overrightarrow{PF_2}|)得到，可设(|PF_1|=4k(k>0))，(|PF_2|=3k)，故(|F_1F_2|=5k)，即(2c=5k)，又由双曲线的定义知道，(|PF_1|-|PF_2|=2a=k) ，则离心率(e=cfrac{2c}{2a}=cfrac{5k}{k}=5)。

(fbox{例4})
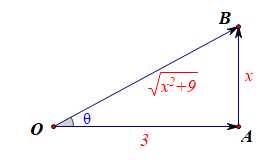
已知向量(overrightarrow{OA}perp overrightarrow{AB})，(|overrightarrow{OA}|=3)，求(overrightarrow{OA}cdot overrightarrow{OB})的值。

分析：设向量(|overrightarrow{AB}|=x)，则(|overrightarrow{OB}|=sqrt{x^2+9})，再设(< overrightarrow{OA} ，overrightarrow{OB}>= heta)，则(overrightarrow{OA}cdot overrightarrow{OB}=|overrightarrow{OA}||overrightarrow{OB}|cos heta=3 imessqrt{x^2+9} imescfrac{3}{sqrt{x^2+9}}=9)

(fbox{例5})已知(vec{a}，vec{b}，vec{c})为平面向量，其中(vec{a}，vec{b})为单位向量，(vec{a}cdot vec{b}=0)，且(vec{a}cdot vec{c}=vec{b}cdot vec{c}=1)，求(|vec{a}+vec{b}+vec{c}|)

分析：由(vec{a}cdot vec{b}=0)，可知(<vec{a}，vec{b}>=90^{circ})，

又(vec{a}cdot vec{c}=vec{b}cdot vec{c}=1)，即(|vec{a}||vec{c}|cos<vec{a}，vec{c}>=|vec{b}||vec{c}|cos<vec{b}，vec{c}>=1)，

即(<vec{a}，vec{c}>=<vec{b}，vec{c}>=45^{circ})，故由(vec{a}cdot vec{c}=1)可知，

(|vec{c}|=sqrt{2})，又(|vec{a}|=1)，(|vec{b}|=1)，

则有(|vec{a}+vec{b}+vec{c}|^2=vec{a}^2+vec{b}^2+vec{c}^2+2vec{a}cdot vec{b}+2vec{a}cdot vec{c}+2vec{b}cdot vec{c}=1+1+2+0+2+2=8)，

故(|vec{a}+vec{b}+vec{c}|=2sqrt{2})。

(fbox{例6})
对任意平面向量(vec{a}，vec{b})，下列关系式不恒成立的是【】

(A.|vec{a}cdot vec{b}|leq |vec{a}||vec{b}|)

分析：恒成立，由于(vec{a}cdot vec{b}=|vec{a}|cdot |vec{b}|cos heta) ，故有(|vec{a}cdot vec{b}|=|vec{a}|cdot |vec{b}||cos heta|leq |vec{a}|cdot |vec{b}|) ；

(B.|vec{a}- vec{b}|leq ||vec{a}|-|vec{b}||)

分析：不恒成立，比如这个反例，(vec{a}=vec{-b})，取为一对相反单位向量，则此时左边为(|2|leq 0)出错。

(C.(vec{a}+ vec{b})^2= |vec{a}+vec{b}|^2)

分析：恒成立，可以按照多项式乘法展开；

(D.(vec{a}+ vec{b})cdot (vec{a}- vec{b})= vec{a}^2-vec{b}^2)

分析：恒成立，可以按照多项式乘法展开；

(fbox{例7})(2017河北武邑中学一模，文11)

在(RtDelta ABC)中，(CA=CB=3)，(M，N)是斜边(AB)上的两个动点，(MN=sqrt{2})，则(overrightarrow{CM}cdot overrightarrow{CN})的取值范围是【】

(A.[2，cfrac{5}{2}];;;;) (B.[2，4];;;;) (C.[3，6];;;;) (D.[4，6];;;;)

分析：求向量的内积的取值范围，应该想到用内积的坐标运算，本题目难点是一般想不到主动建系，由形的运算转化为数的运算。

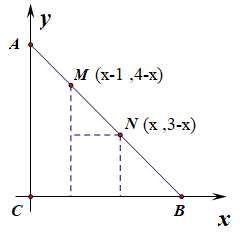
解：如图所示，以点(C)为坐标原点，分别以(CB、CA)所在的直线为(x、y)轴建立如同所示的坐标系，
则(C(0，0))，(A(0，3))，(B(3 ，0))，设点(N)的横坐标为(x)，则由等腰直角三角形可知，点(N)的纵坐标为(3-x)，即点(N(x，3-x))，

又由(MN=sqrt{2})，计算可知点(M(x-1，4-x))，则(overrightarrow{CM}=(x-1，4-x))，(overrightarrow{CN}=(x，3-x))，

由于点(M,N)是动点，取两个极限位置研究(x)的取值范围，当点(M)位于点(A)时，(x)取到最小值(1)，当点(N)位于点(B)时，(x)取到最大值(3)，即(1leq xleq 3)，

则(overrightarrow{CM}cdot overrightarrow{CN}=f(x)=((x-1，4-x)cdot (x，3-x)=x(x-1)+(4-x)(3-x)=2(x-2)^2+4)，(xin [1，3])

当(x=2)时，(f(x)_{min}=f(2)=4)，当(x=1)或(x=3)时，(f(x)_{max}=f(1)=f(3)=6)，即(f(x)in [4，6])。故选D。

(fbox{例8})(2017辽宁沈阳二模)

已知向量(overrightarrow{OA}=(3，1))，(overrightarrow{OB}=(-1，3))，(overrightarrow{OC}=moverrightarrow{OA}-noverrightarrow{OB}(m>0，n>0))，若(m+nin [1，2])，则向量(overrightarrow{OC})的取值范围是【】

(A.[sqrt{5}，2sqrt{5}];;;;) (B.[sqrt{5}，2sqrt{10});;;;) (C.(sqrt{5}，sqrt{10});;;;) (D.[sqrt{5}，2sqrt{10}])

解：(overrightarrow{OC}=moverrightarrow{OA}-noverrightarrow{OB}=m(3，1)-n(-1，3)=(3m，m)-(-n，3n)=(3m+n，m-3n))，

故(|overrightarrow{OC}|=sqrt{(3m+n)^2+(n-3m)^2}=sqrt{10m^2+10n^2}=sqrt{10}sqrt{m^2+n^2})

【预备知识】已知(m>0，n>0 ，m+nin [1，2])，求(m^2+n^2)的取值范围。

分析：将上述给定的数的条件转化为形的条件，则(m^2+n^2)可以看成半径为(r)的动圆上位于第一象限内的一点，(1leq m+nleq 2)可以看成两条平行线(m+n=1)和(m+n=2)之间的平面区域内且位于第一象限的的任意一点，

故(m^2+n^2)的取值范围：最小值可以看成圆心((0，0))到直线(m+n=1)的距离的平方，最大值可以看成圆心((0，0))到直线(m+n=2)的距离的平方，

则可知(d_1=cfrac{1}{sqrt{2}})，(d_2=cfrac{2}{sqrt{2}})，故(d_1^2=cfrac{1}{2})，(d_2^2=2)，即(m^2+n^2in [cfrac{1}{2}，2])；

接上可知，(|overrightarrow{OC}|=sqrt{10}sqrt{m^2+n^2}in [sqrt{5}，2sqrt{5}])，故选A。

【引申】已知(m>0，n>0 ，m+nin [1，2])，求((m+1)^2+(n+1)^2)的取值范围。

分析：即故((m+1)^2+(n+1)^2)的取值范围：最小值可以看成点((-1，-1))到直线(m+n=1)的距离的平方，最大值可以看成点((-1，-1))到直线(m+n=2)的距离的平方；