ds第五章学习记录

Posted 2020-12-23 drgnibasaw

二叉树性质

在二叉树的 第l层上至多有2i-l 个结点

深度为K的 二叉树至多有 2k -1 个结点 

对任何一棵二叉树T, 如果其终端结点数为n。度为2的结点数为n2 则n。= n2+1。

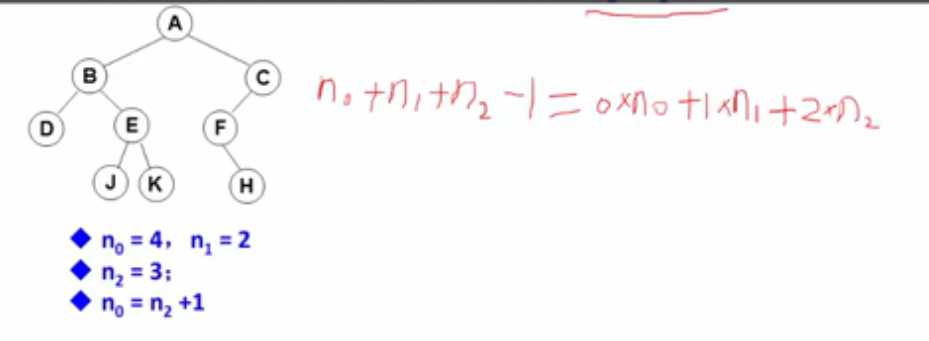  （结点-1=边）

具有 n 个结点的完全二叉树的深度为llog心+ 1 

    

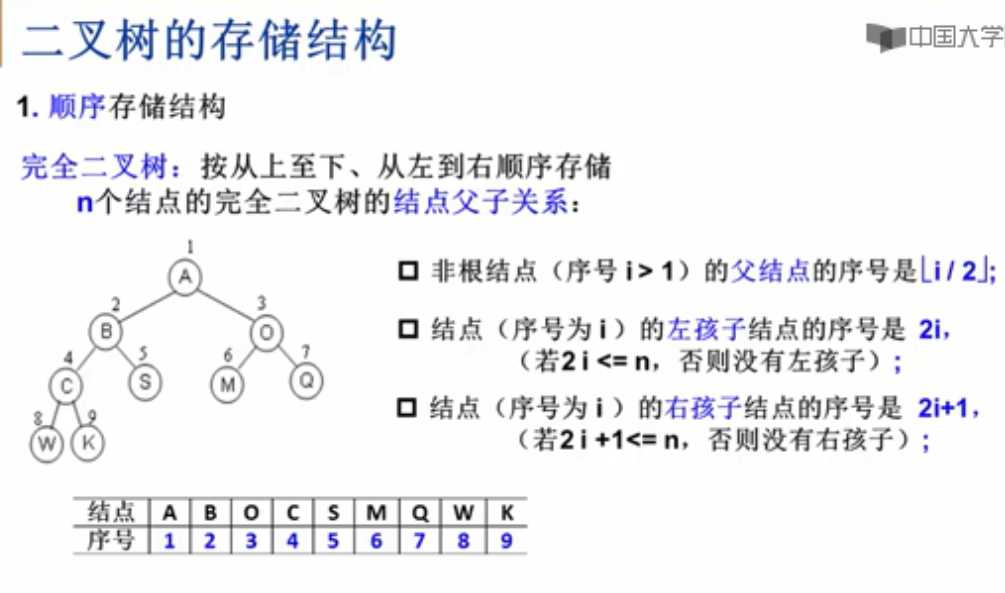
一般二叉树用数组存储 易造成空间浪费

 

 

 

 

 

 

 

课堂笔记

1. 一个具有258个结点的二叉树的高h为？   最高 斜二叉树 258       最矮 完全二叉树 9
2. 深度为h的满m叉树的第k层有多少个结点?(1<=k<=h)      m^(k-1）
3. 在一棵度为3的树T中,若有10个度为3的结点,1个度为2的结点,10个度为1的结点,则树T叶子结点个数为？

除了根节点之外，树的每个节点都有唯一的一个入度，因此计算出共有多少个出度，+1=总节点数目。20+2+20+1=43   结点总数 = 分支总数+1

 

课堂笔记

1. typedef的问题

2. 堆与栈的内存分配      为什么cin>>n;  new BiTree[n]可以但是int a[n]不可以？

      

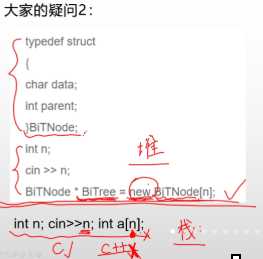
3.       类型定义 注意结点                                                                                                                

4. list leaves  层次遍历                                                                                                                                                                                                                          二叉链表表示                         遍历 先存储 （保留孩子）先进先出 --->队列模板stl  queue入队类型？变量名？       queue<BiTNode *>q;                                          front pop push  +栈/+队列  作为中间辅助数据结构解决问题                                                                                                                                                                

 

• 个人问答题                                                                                                                                                                                                                                           用结构体数组储存二叉树的中序遍历     {char data; int lchild; int rchild; }BiNode； BiNode[] t +int root                                                                                               递归中序遍历： 只关注本层逻辑！       递进到终止条件 回推到这一层

void MidOrder(BiTree[] t,int root)
{
	int l,r,i=root;
	l=t[i].lchild;
	r=t[i].rchild;
	
	if(l)  MidOrder(t,l);
	cout<<t[i].data;
	if(r)  MidOrder(t,r);
			
}

　 

• 树的同构                                                                                                                                                                                                                                               给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2，则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的，因为我们把其中一棵树的结点A、B、G的左右孩子互换后，就得到另外一棵树

 

• • 用new运算符动态分配一个长度为n的整型数组

 

 

• • 树不为空的情况
    • 结点的数据不相等（不同构） 
    • 结点数据相等继续比较左左孩子和右右孩子（若都同构则两棵树同构） 
    • 结点数据相等但左左孩子和右右孩子不同构则继续比较左右和右左孩子（若都同构则两棵树同构） 
    • 结点数据相等但左左右右，左右右左都不同构则两棵树不同构
  • 树为空的情况 root就返回-1 

 

参考资料https://www.cnblogs.com/jingjing1234/p/10822040.html

 

• 小组合作0528---找到最深的叶结点

1. 转换成层次储存 直接遍历输出
2. 调用递归 先利用check数组找到根结点 从根节点一直调用函数递归至叶子结点 每调用一次+1   递进到终止条件 回推到这一层
3. 我们组的算法比较傻 时间复杂度也很高         改进--->算法 new动态数组

ruolin小组的递归

int depth(bitnode tree[],int ownnum)
 {
  if(tree[ownnum].num==0)//到底了
    return 0;
    
  int max=0;
 
  for(int i=0;i<tree[ownnum].num;i++)
  {//遍历每个孩子，寻找孩子中的最大值
   int childdepth=depth(tree,tree[ownnum].child[i])+1;//每递归一次深度加一，得到目前结点的深度
   if(childdepth>max)
   max=childdepth;
  }
 
  return max;//返回当前深度给上一层

 }

　　改进方向 其他小组意见

 

 

 

哈哈记得要释放空间啊