《非线性泛函分析导论:拓扑方法导论》
Posted cx2016
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了《非线性泛函分析导论:拓扑方法导论》相关的知识,希望对你有一定的参考价值。
非线性泛函分析导论(三):拓扑方法导论
这一节详细讨论拓扑方法。其中 Brouwe 拓扑度的基本使用方法在之前介绍流形的环绕时我们已经接触过。Brouwer 度是拓扑学中的重要工具,但对于泛函分析而言,我们需要将其延伸至无限维空间。这就是Leray-Schaulder 拓扑度。











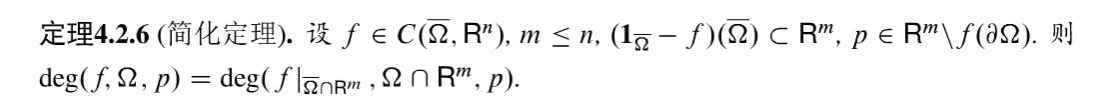



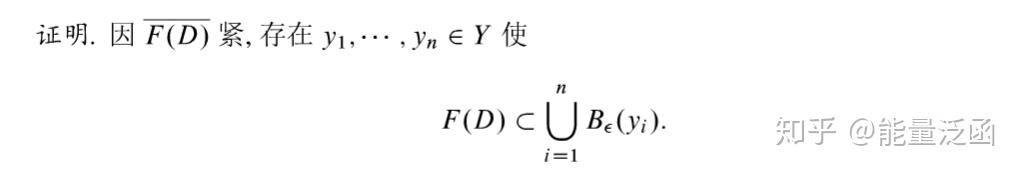
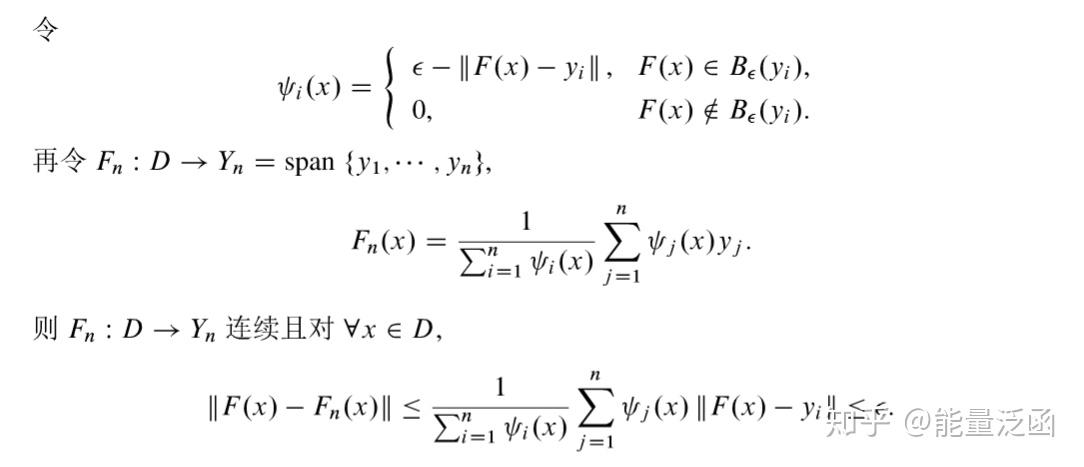






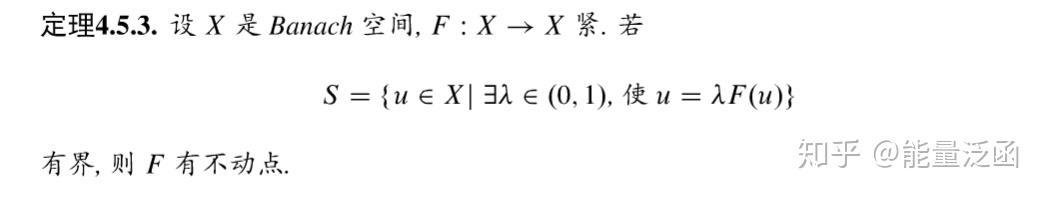










写下你的评论...
全文完
本文由 简悦 SimpRead 优化,用以提升阅读体验
使用了 全新的简悦词法分析引擎 beta,点击查看详细说明
以上是关于《非线性泛函分析导论:拓扑方法导论》的主要内容,如果未能解决你的问题,请参考以下文章
《非线性泛函分析导论(完): 形变定理与 MinMax 原理》