AVL树

Posted 2020-12-23 happyknockoncode

AVL树

AVL树是平衡二叉搜索树，比普通二叉搜索树多了一个平衡功能；

当一个节点的左子树与右子树的高度差超过1时 ，就被认为是不平衡的。然后通过旋转二叉树维持平衡。

插入操作

左节点的左子树插入操作（单旋转）插入5号：

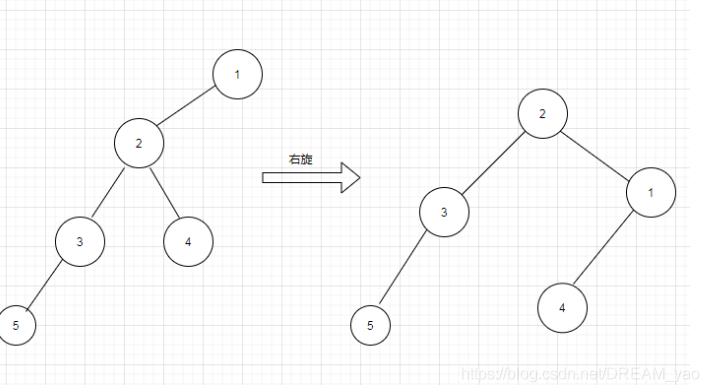
左节点的右子树插入操作（双旋转）插入5号：

]

删除操作：

需要删除一个节点时，若只有一个子节点或无子节点，直接替换即可，若有两个子节点，则要判断左右子树的高度，用最高的子树去覆盖要删除的节点，然后释放子树上的节点空间，调整平衡即可。

当删除一个节点后，判断树的高度，若破坏了平衡，则调整平衡；

撸代码：

  1/**
  2把二叉树的任何节点的左子树高度减去右子树高度定义为
  3该节点的平衡因子。二叉平衡树的平衡因子只能是1、0或者-1。
  4
  5一、单旋转
  61.左节点的左子树插入操作 右旋转
  72.右节点的右子树插入操作 左旋转
  8
  9二、双旋转
 101.左节点的右子树插入操作 先左后右旋转
 112.右节点的左子树插入操作 先右后左旋转
 12*/
 13
 14#include<stdio.h>
 15#include<iostream>
 16#include<algorithm>
 17using namespace std;
 18typedef struct AvlNode
 19{
 20    int data;
 21    AvlNode *m_pLeft;
 22    AvlNode *m_pRight;
 23    int height;
 24}*AvlTree,*Position,AvlNode;
 25int Height(AvlTree T)
 26{
 27    if(NULL==T)
 28        return -1;/**为了使差==2 直线情况*/
 29    else
 30        return T->height;
 31}
 32/**单旋转右旋*/
 33AvlTree Right(AvlTree T)
 34{
 35    AvlTree L=T->m_pLeft;
 36    T->m_pLeft=L->m_pRight;
 37    L->m_pRight=T;
 38    T->height=max(Height(T->m_pLeft),Height(T->m_pRight))+1;
 39    L->height=max(Height(L->m_pLeft),Height(L->m_pRight))+1;
 40    return L;/**L成为根节点*/
 41}
 42/**单旋转左旋*/
 43AvlTree Left(AvlTree T)
 44{
 45    AvlTree R=T->m_pRight;
 46    T->m_pRight=R->m_pLeft;
 47    R->m_pLeft=T;
 48    T->height=max(Height(T->m_pLeft),Height(T->m_pRight))+1;
 49    R->height=max(Height(R->m_pLeft),Height(R->m_pRight))+1;
 50    return R;/**R成为根节点*/
 51}
 52/**双旋转 先左旋后右旋*/
 53AvlTree doubleRight(AvlTree T)
 54{
 55    T->m_pLeft=Left(T->m_pLeft);
 56    return Right(T);
 57}
 58/**双旋转 先右后左*/
 59AvlTree doubleLeft(AvlTree T)
 60{
 61    T->m_pRight=Right(T->m_pRight);
 62    return Left(T);
 63}
 64AvlTree AvlTreeInsert(AvlTree T,int x)
 65{
 66    if(T==NULL)/**设立根节点*/
 67    {
 68        T=(AvlNode *)malloc(sizeof(struct AvlNode));
 69        if(T)
 70        {
 71            T->data=x;
 72            T->m_pLeft=T->m_pRight=NULL;
 73            T->height=0;
 74        }
 75        else
 76        {
 77            printf("ERROR
");
 78            exit(0);
 79        }
 80    }
 81    else if(x<T->data)/**插入左子树*/
 82    {
 83        T->m_pLeft=AvlTreeInsert(T->m_pLeft,x);/**先插入，后旋转*/
 84
 85        /**不平衡*/
 86        if(Height(T->m_pLeft)-Height(T->m_pRight)==2)
 87        {
 88            if(x<T->m_pLeft->data)/**左节点的左子树插入操作 右旋转*/
 89            {
 90                T=Right(T);
 91            }
 92            else
 93            {
 94                T=doubleLeft(T);
 95            }
 96        }
 97    }
 98    else if(x>T->data)
 99    {
100        T->m_pRight=AvlTreeInsert(T->m_pRight,x);
101        if(Height(T->m_pRight)-Height(T->m_pLeft)==2)
102        {
103            if(x>T->m_pRight->data)/**右节点的右子树 左旋*/
104            {
105                T=Left(T);
106            }
107            else
108            {
109                T=doubleRight(T);
110            }
111        }
112    }
113    T->height=max(Height(T->m_pLeft),Height(T->m_pRight))+1;
114    return T;
115}
116AvlTree AvlTree_min(AvlTree T)
117{
118    if(T->m_pLeft==NULL)
119        return T;
120    else return AvlTree_min(T->m_pLeft);
121}
122AvlTree AvlTree_max(AvlTree T)
123{
124    if(T->m_pRight==NULL)
125        return T;
126    else return AvlTree_max(T->m_pRight);
127}
128
129/**删除 z 节点，返回根节点*/
130AvlTree deleteNode(AvlTree tree,AvlNode *z)
131{
132    if(tree==NULL||z==NULL)
133        return NULL;
134    /**待删除节点在tree的左子树上*/
135    if( z->data < tree->data )
136    {
137        tree->m_pLeft=deleteNode(tree->m_pLeft,z);
138        /**删除tree左子树节点后 ，调节AVL树平衡*/
139        /**在tree树上调整平衡*/
140        if(Height(tree->m_pRight)-Height(tree->m_pLeft)==2)
141        {
142            /**画图即可明白*/
143            AvlNode *r=tree->m_pRight;
144            if(Height(r->m_pLeft)>Height(r->m_pRight))
145                tree=doubleLeft(tree);
146            else
147                tree=Left(tree);
148        }
149    }
150    else if( z->data > tree->data )
151    {
152        /**删除tree右子树，调整平衡*/
153        tree->m_pRight=deleteNode(tree->m_pRight,z);
154        if(Height(tree->m_pLeft)-Height(tree->m_pRight)==2)
155        {
156            AvlNode *l=tree->m_pLeft;
157            if(Height(l->m_pRight)>Height(l->m_pLeft))
158                tree=doubleRight(tree);
159            else
160                tree=Right(tree);
161        }
162    }
163    else /**当前删除节点*/
164    {
165        /**左右孩子都有*/
166        if((tree->m_pLeft)&&(tree->m_pRight))
167        {
168            if(Height(tree->m_pLeft)>Height(tree->m_pRight))
169            {
170                /**若左子树较高
171                1 找出左子树最大节点
172                2 最大节点覆盖tree节点
173                3 删除这个叶子最大节点
174                这样尽量可保持平衡
175                */
176                AvlNode *Max =AvlTree_max(tree->m_pLeft);
177                tree->data=Max->data;
178                tree->m_pLeft=deleteNode(tree->m_pLeft,Max);
179            }
180            else
181            {
182                /**同理：找到右子树最小节点覆盖即可*/
183                AvlNode *Min=AvlTree_min(tree->m_pRight);
184                tree->data=Min->data;
185                tree->m_pRight=deleteNode(tree->m_pRight,Min);
186            }
187        }
188        else
189        {
190            /**只有一个孩子节点，直接接上即可*/
191            AvlNode *temp=tree;
192            tree=tree->m_pLeft?tree->m_pLeft:tree->m_pRight;
193            free(temp);
194        }
195    }
196    return tree;
197}
198
199void Find(AvlTree p)
200{
201    if(p)
202    {
203        printf("根节点 %d ",p->data);
204        if(p->m_pLeft)
205            printf("左儿子：%d ",p->m_pLeft->data);
206        if(p->m_pRight)
207            printf("右儿子：%d ",p->m_pRight->data);
208        printf("
");
209        Find(p->m_pLeft);
210
211        Find(p->m_pRight);
212    }
213}
214AvlTree getNode(AvlTree T,int x)
215{
216    while(T&&T->data!=x)
217    {
218        if(T->data>x)
219            T=T->m_pLeft;
220        else
221            T=T->m_pRight;
222    }
223    return T;
224}
225int main()
226{
227    AvlTree root = NULL;
228    for(int i=1;i<=5;i++)
229    {
230        root = AvlTreeInsert(root,i);
231    }
232    Find(root);
233    printf("
*****************
");
234    root=deleteNode(root,getNode(root,1));
235    Find(root);
236    return 0;
237}

学习博客：https://www.cnblogs.com/skywang12345/p/3576969.html
https://www.cnblogs.com/zhuwbox/p/3636783.html