单调栈

Posted 2020-12-23 r1-12king

1、分类

• 单调递增栈：数据出栈的序列为单调递增序列
• 单调第减栈：数据出栈的序列为单调递减序列

 

2、操作（以单调递增栈为例）

• 如果新元素比栈顶元素大， 入栈
• 如果新元素比栈顶元素小，栈顶元素出栈，直到栈顶元素小于该元素，入栈该元素

 

3、示例

例如，给定一个序列 [ 1, 3, 5, 2, 4 ]，当1，3，5入栈以后，当遇到新元素2时，由于栈顶元素5 > 2， 5被弹出， 新元素2是出栈元素5右边第一个比 5 小的元素，即新元素是出栈元素向后找第一个比其小的元素；此时新栈顶元素为3，3是5左边第一个比5小的数字，即新栈顶元素是出栈元素向前找第一个比其小的元素。

 

 

 

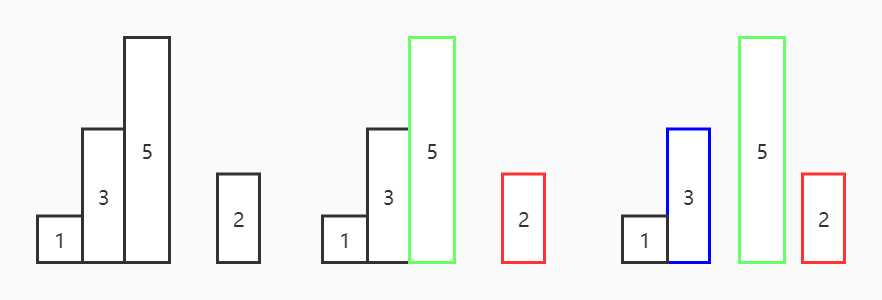
4、代码块

stack = []
for i in range(len(nums)):
    while stack and stack.top() > nums[i]:
        stack.pop()
    stack.push(nums[i])

 

5、应用

a.柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。求在该柱状图中，能够勾勒出来的矩形的最大面积。

 

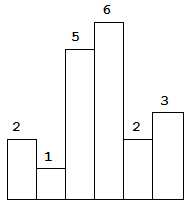
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

 

 

 

 

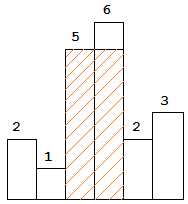
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

 

思路

1. 1. 对于一个高度，如果能得到向左和向右的边界
   2. 那么就能对每个高度求一次面积
   3. 遍历所有高度，即可得出最大面积
   4. 使用单调栈，在出栈操作时得到前后边界并计算面积

代码：

"""
为了方便计算，将栈内存储的是元素的位置
"""
class Solution:
    def largestRectangleArea(self, heights):
        height = [0] + heights + [0]
        lens = len(height)
        maxs = 0
        for i in range(1, lens - 1):
            left = i
            right = i
            for j in range(i - 1, -1, -1):
                if height[j] < height[i]:
                    left = j
                    break
            for k in range(i + 1, lens):
                if height[k] < height[i]:
                    right = k
                    break
            maxs = max(maxs, height[i] * (right - left - 1))

        return maxs

View Code