「网络流 24 题」魔术球 的贪心做法和证明

Posted 2020-12-23 cyx0406

https://loj.ac/problem/6003

https://www.luogu.com.cn/problem/P2765

假设有 (n) 根柱子，现要按下述规则在这 $ n $ 根柱子中依次放入编号为 $ 1, 2, 3, 4, cdots $ 的球。

1. 每次只能在某根柱子的最上面放球。
2. 在同一根柱子中，任何 (2) 个相邻球的编号之和为完全平方数。

试设计一个算法，计算出在 $ n $ 根柱子上最多能放多少个球。

(n leq 55)

一、 DAG 的最小路径覆盖做法

从小到大枚举答案，动态在和为平方数的数对中加边，相当于判断 DAG 上的最小路径覆盖数是否 (leq n)。

求 DAG 上的最小路径覆盖，可以将每个点拆成一个入点和一个出点，对于原图的边 ((u,v))，我们就从 (u) 的出点连向 (v) 的入点，注意一个点只能有至多一个入边和一个出边，于是转化成总点数减去二分图最大匹配。

实际测试出来，最后答案最大为 (1567)。

二、 贪心另解

本题还有一个贪心做法，值得探究。

这个贪心做法是这样的：每次和当前的每根柱子的顶部的球求和，判断能否放上去，能放就直接放上去，不能放就不放。

证明参考：http://kczno1.blog.uoj.ac/blog/2724

可以证明。用数学归纳法证明贪心法每次的选择是唯一的(即，只能把球放到0或1个已经放了球的柱子上)，且答案为(一个简单式子，暂不剧透)。用Dilworth定理可以证明这个是最优的(hint:柱子的顶端构成一个反链)。 这个算法work是因为“加起来是平方数”的性质很好。改成其他条件就做不了了。

具体的证明：

同样若 (a<b) 且 (a+b) 为完全平方数，我们连边 (a o b)。

首先归纳证明选择方案唯一（即对于每个 (x)，如果有放在它上面的球，那么一定是 (x) 的出边中编号最小的点），这里只讲关键归纳步骤。

假设 (a<b<c)，现在要加入 (c)。即假设 (a,b) 出边中最小的点都是 (c)，设 (a+c=x^2,b+c=y^2)。那么有下图的大小关系：

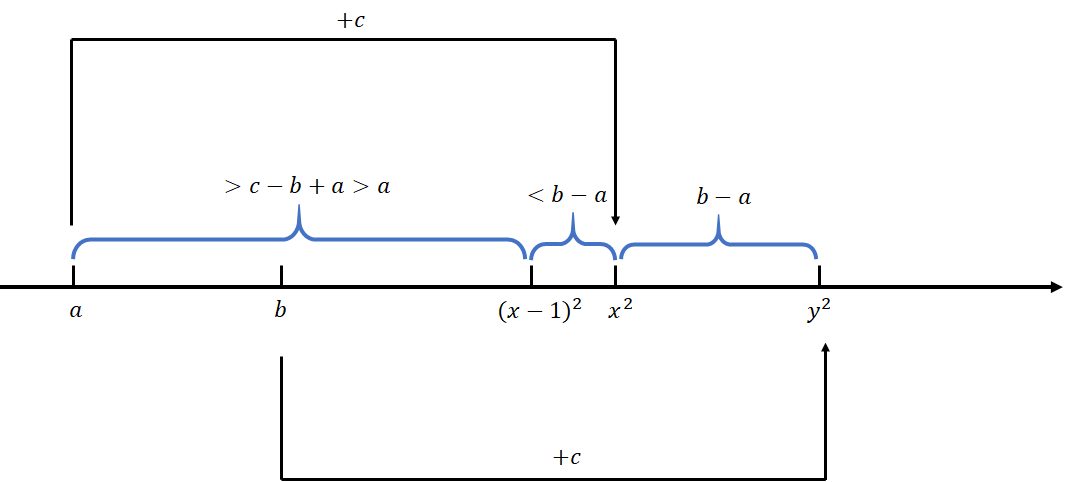
我们发现 (x^2-(x-1)^2<y^2-x^2=b-a)，于是 ((x-1)^2-a>c-b+a>a)，那么 (a) 一定可以连向一个更小的点 ((x-1)^2-a)。因此按照这种策略，每次都至多只能找到一个合法位置放在它上面。

同时我们也能证明柱子的顶端那些数构成一个反链。而根据 Dilworth 定理，任意反链 $leq $ 最小链覆盖 $leq $ 最小路径覆盖，因此这是最优解。