视觉SLAM三维空间刚体运动的描述

Posted 2020-12-22 guoben

本文将一步一步探索如何描述三维空间中的刚体运动（平移+旋转）。

1.点与坐标系

在2D平面中，两个向量之间的变换可以用两个坐标加旋转角表达；
在3D空间中描述刚体需要一些别的概念来描述（略写），主要有：坐标系（参考系）；点；向量；向量的坐标。

2.旋转矩阵

考虑一次旋转：坐标系(（e1,e2,e3))发生了旋转，变成(e_1‘,e_2‘,e_3‘))，而向量a不动，那么它的坐标如何变化?


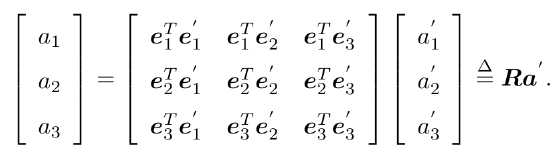
其中，??称为旋转矩阵,可以验证：
? R是一个正交矩阵；
? R的行列式为+1。
? 满足这两个性质的矩阵称为旋转矩阵

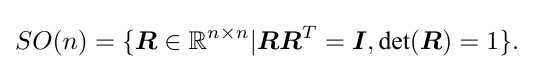
?Special Orthogonal Group 特殊正交群
于是，1到2的旋转可表达为：(??_1=??_{12}??_2)，反之：(??_2=??_{21}??_1)。(要注意下标顺序)
矩阵关系：(??_{21}=??_{12}^{?1}=??_{12})

3.旋转向量和欧拉角

旋转向量

除了旋转矩阵/变换矩阵之外，还存在其他的表示方式；旋转矩阵R有九个元素，但仅有三个自由度；能否以更少的元素表达旋转？

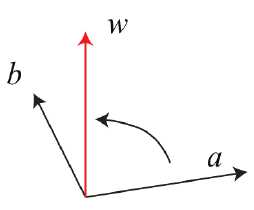
旋转向量：1.方向为旋转轴，长度为转过的角度；2.称为角轴/轴角（AngleAxis）或旋转向量（RotationVector）。
旋转向量与矩阵的不同：1.它仅有三个量 ；2.无约束；3. 更直观。它们可以是同一个旋转的不同表达方式。
罗德里格斯公式（Rodrigues’sFormula）：

[R=cos{ heta I} + (1-cos heta )nn^T + sin{ heta n^(^)} ]

（可以想办法证明这个公式）
?旋转矩阵转向量：

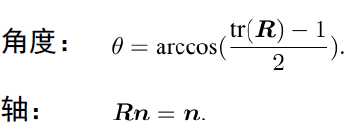
欧拉角

欧拉角（ Euler Angles)
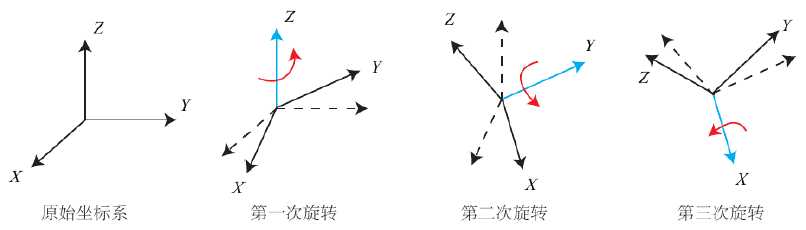
将旋转分解为三个方向上的转动例，按Z-Y-X顺序转动
轴可以是定轴或动轴，顺序亦可不同
常见的有：yaw-pitch-roll，东北天
不同领域的习惯有所不同
1.绕物体的乙轴旋转，得到偏航角yaw
2.绕旋转之后的Y轴旋转，得到俯仰角 pitch
3.绕旋转之后的X轴旋转，得到滚转角roll。

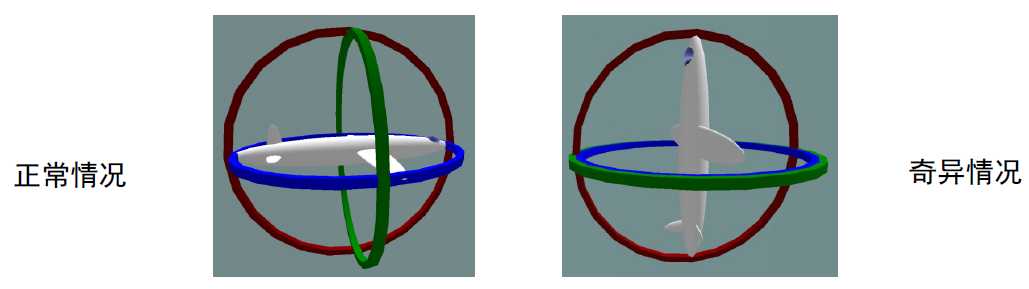
万向锁

• 欧拉角的奇异性问题
• 在特定值时，旋转自由度减1
• Yaw- pitch-rol顺序下，当 pitch为90度时，存在奇异性
  

4.四元数

旋转矩阵用9个量描述3自由度的旋转，具有冗余性；欧拉角和旋转向量是紧凑的，但具有奇异性。事实上，我们找不到不带奇异性的三维向量描述方式[19]。这有点类似于用两个坐标表示地球表面（如经度和纬度），将必定存在奇异性（纬度为+-90? 时经度无意义）。

四元数的描述

一个四元数q 拥有一个实部和三个虚部。如下：
(q = q_0 + q_1i + q_2j + q_3k);
其中i; j; k 为四元数的三个虚部。这三个虚部满足以下关系式：

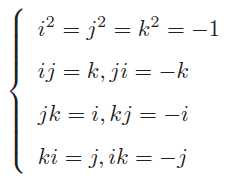
如果把i; j; k 看成三个坐标轴，那么它们与自己的乘法和复数一样，相互之间的乘法和外积一样。有时人们也用一个标量和一个向量来表达四元数：
(q = [s; v]^T, s = q_0 in R, v = [q_1; q_2; q_3]^Tin R^3)
这里，s称为四元数的实部，而v称为它的虚部。如果一个四元数的虚部为0，称之为实四元数。反之，若它的实部为0，则称之为虚四元数

四元数的运算

四元数和通常复数一样，可以进行一系列的运算。常见的包括四则运算、数乘、求逆、共轭等。下面将分别介绍。
现有两个四元数(q_a,q_b)，它们的向量表示为([s_a; v_a]T; [s_b; v_b]T)，或者原始四元数表示为：
(q_a = s_a + x_ai + y_aj + z_ak; q_b = s_b + x_bi + y_bj + z_bk).

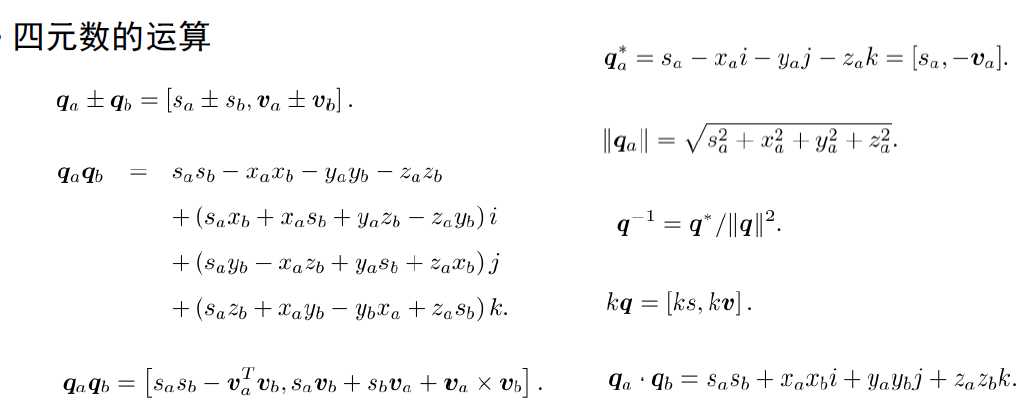
四元数到角轴：(q=[cos( heta/2).n_xsin( heta/2),n_ysin( heta/2),n_zsin( heta/2)])
角轴到四元数：

[egin{cases} heta = 2arccos(q_0)|n_x,n_y,n_z|^T=[q_1,q_2,q_3]^T/sin(frac{ heta}{2}) end{cases} $]