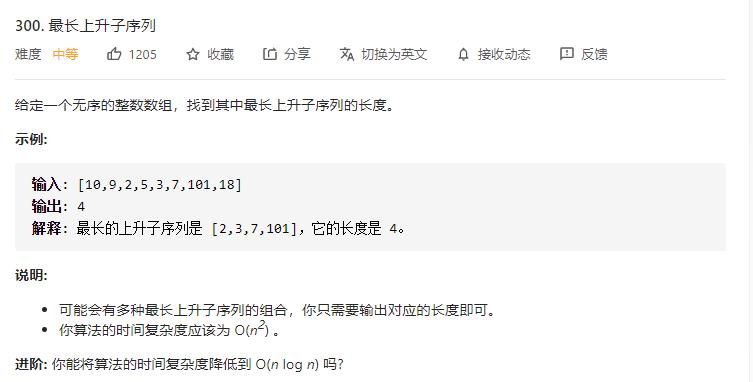
300. 最长上升子序列

Posted 2020-12-22 jmhwsrr

题目

方法一：动态规划

我们可以维护一个数组(dp[])，(dp[i])表示以(nums[i])为结尾元素的最长上升子序列的长度。在计算(dp[i])之前，我们已经计算出了(dp[0....i-1])的值，考虑在(num[i])之前的最长子序列的尾部加上(nums[i])， (dp[j])代表(nums[0...j-1])中最长上升子序列的长度，如果(dp[i])能够从(dp[j])这个状态转移过来，则要求(nums[i])必须大于(nums[j])。其状态转移方程为：

[dpleft[i ight] = maxleft(dpleft[j ight] ight) + 1,其中0<j<i,且nums[j]<nums[i] ]

代码实现：

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int n = (int)nums.size();
        if (n == 0) return 0;

        vector<int> dp(n, 0);
        dp[0] = 1;

        for (int i = 1; i < nums.size(); i++){
            dp[i] = 1;
            for (int j = 0; j < i; j++){
                if (nums[i] > nums[j]){
                    dp[i]  = max(dp[i], dp[j]+1);
                }
            }
        }

        return *max_element(dp.begin(), dp.end());
    }
};

方法二：贪心+二分查找

这个暂时没有理解，待下次理解。
题解地址：https://leetcode-cn.com/problems/longest-increasing-subsequence/solution/zui-chang-shang-sheng-zi-xu-lie-by-leetcode-soluti/

提交结果