构造哈夫曼树的过程

Posted 2020-12-21 gmengshuai

构造赫夫曼树

以下所有都是根据代码形成的流程，便于理解，阅读代码请移步

赫夫曼树-构造-编码-译码

1. 定义结点结构体

2. 定义结点结构体数组

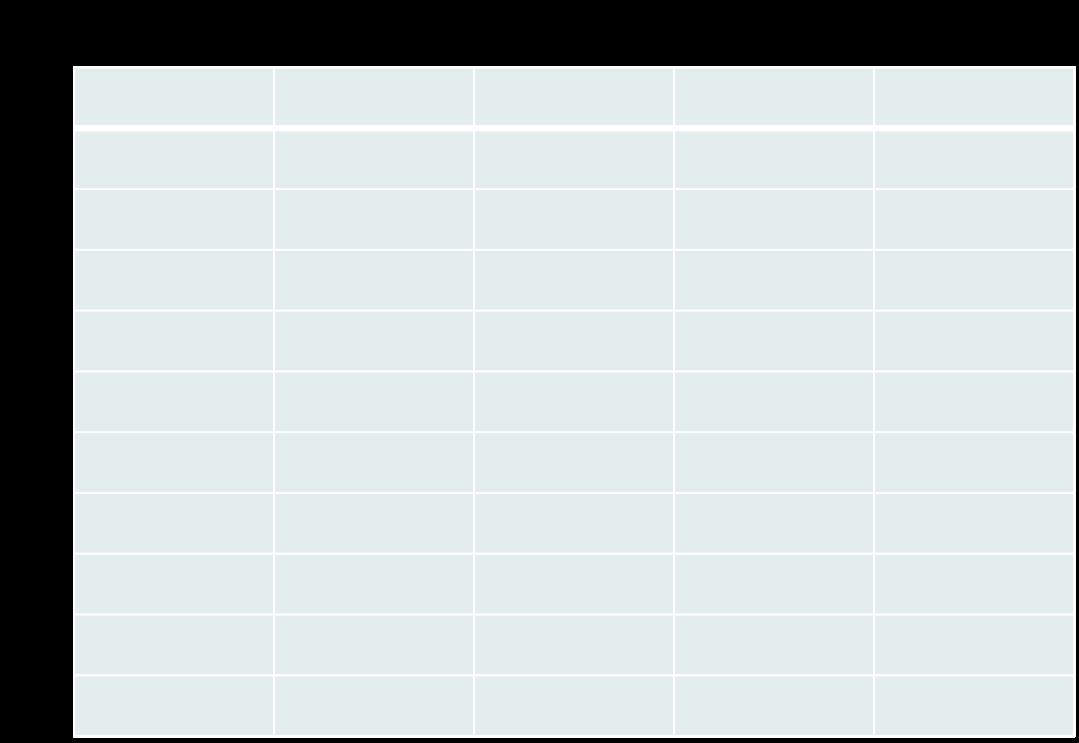
3. 初始化

? 权植为0，双亲及左右孩子为-1

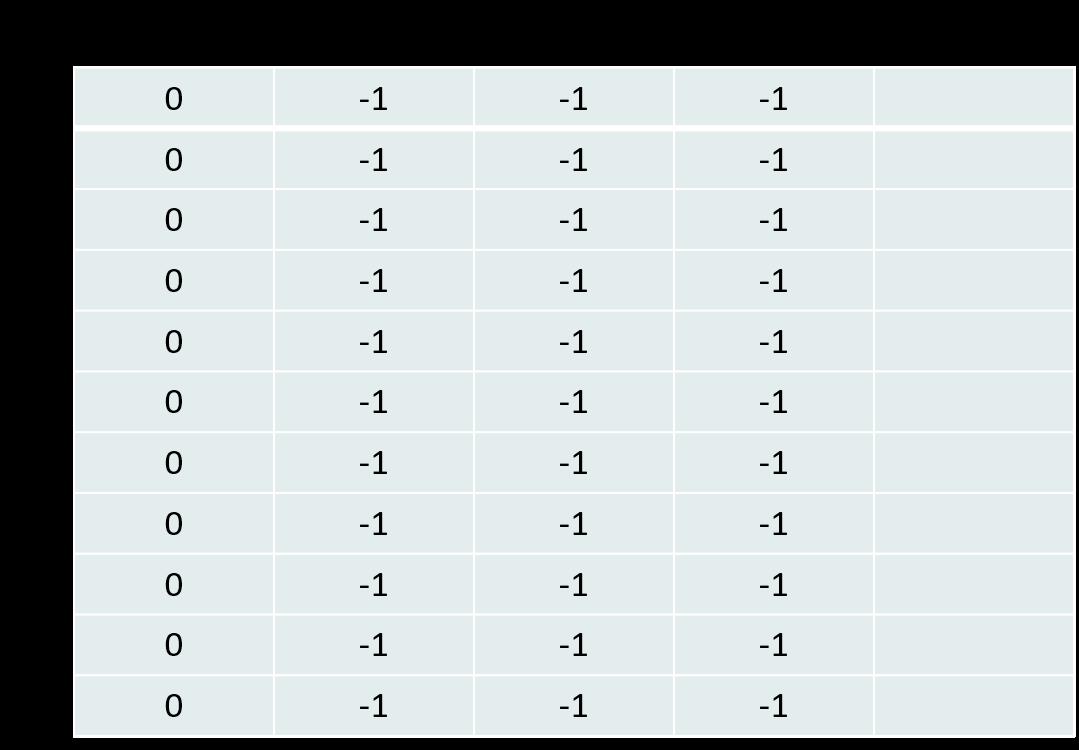
4. 输入叶子结点及其权植

? 假如输入叶子个数n为6

? 输入6个 叶子结点 及其 权植

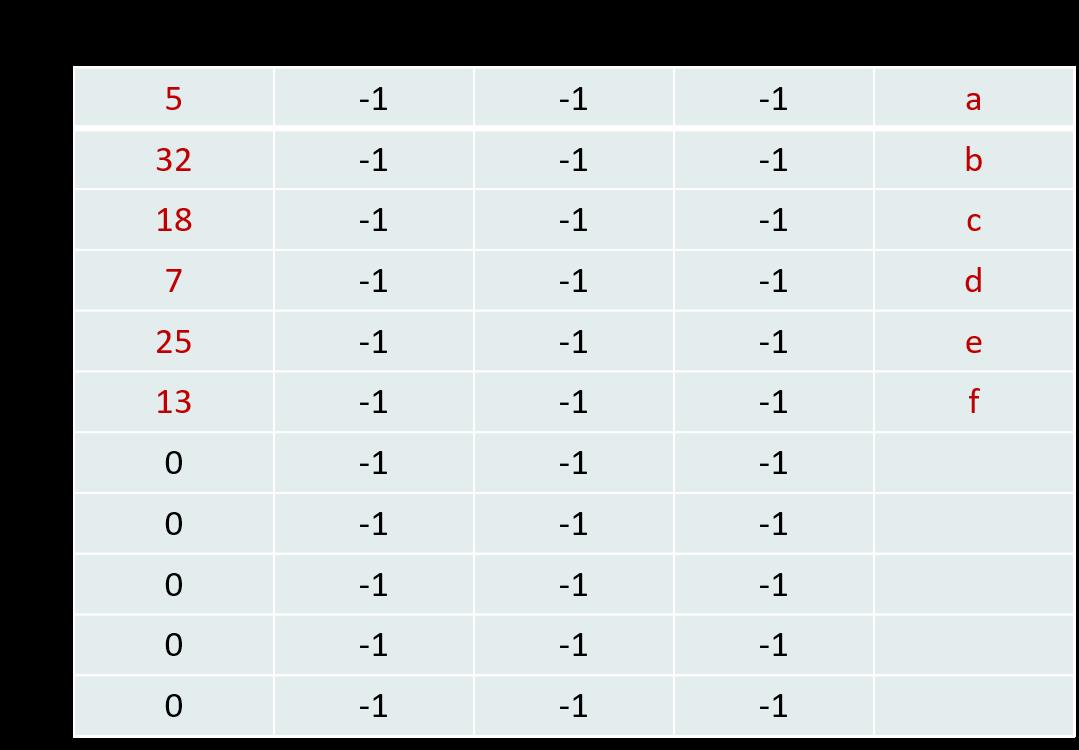
5. 找最小和次小权植

从叶子结点中找最小和次小权植【这些叶子结点包括合并产生的结点】

m1、m2中分别存放两个无父结点且结点权值 最小和次小 的两个结点
x1、x2分别对应m1和m2的下标值

m1 = m2 = MAXVALUE
x1 = x2 = 0

第1轮：

m1 = 5	m2 = 7
x1 = 0	x2 = 3

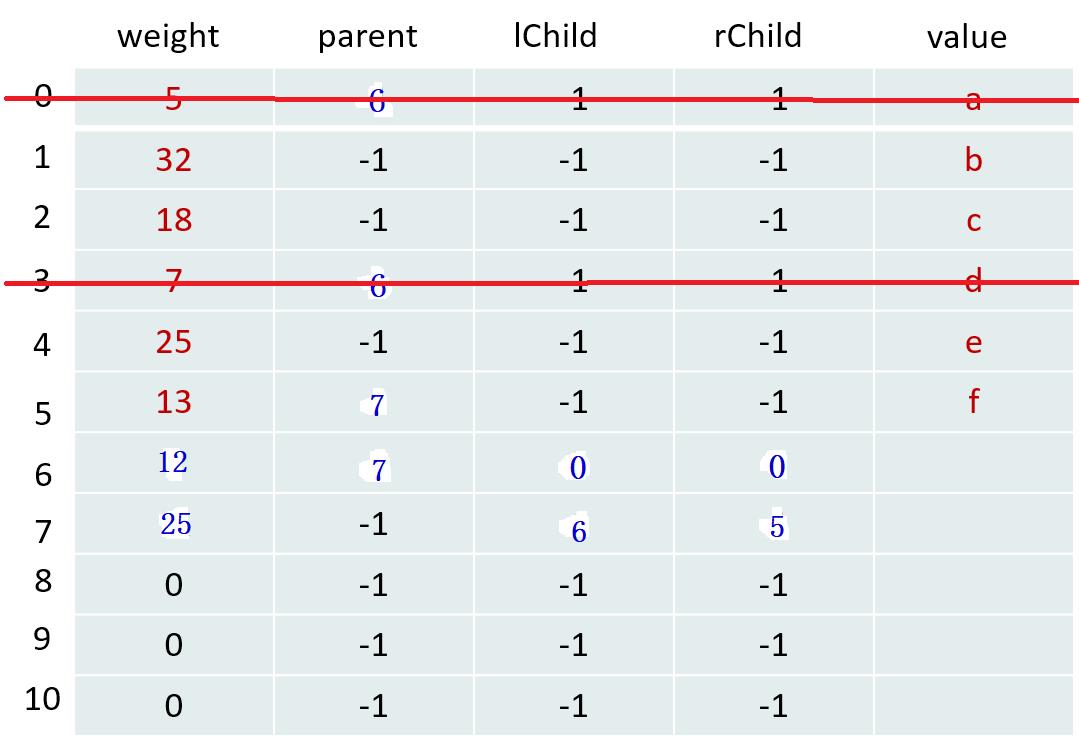
更新树的信息【相当于填表】

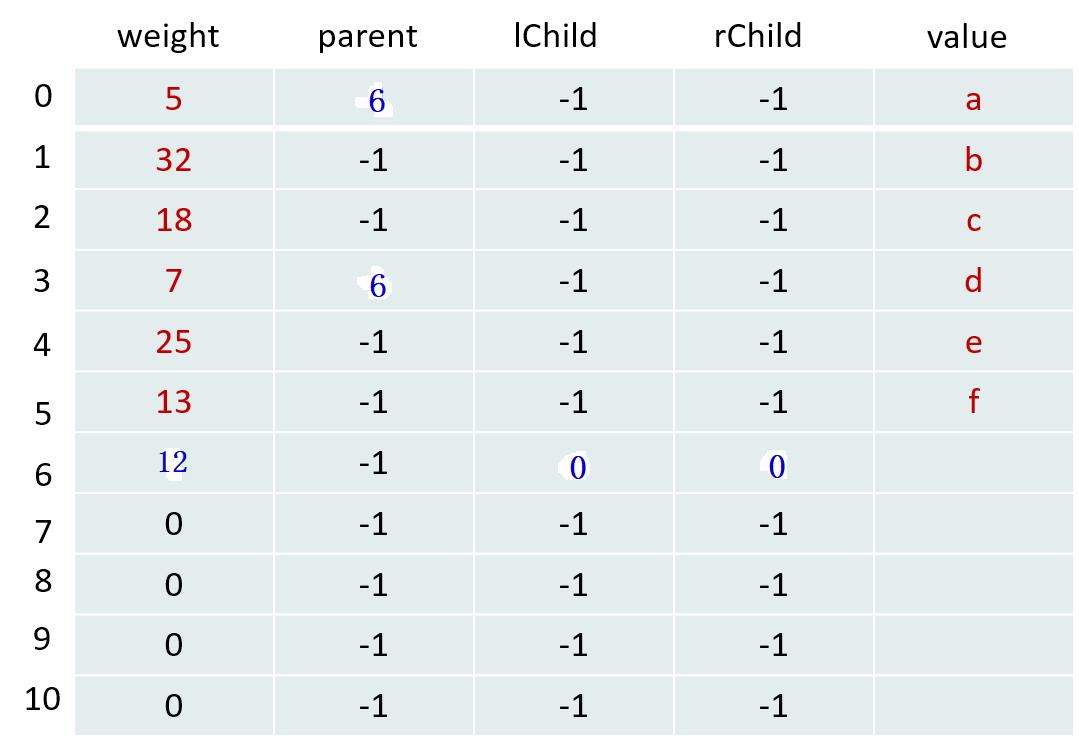
第2轮：

m1 = 12	m2 = 13
x1 = 6	x2 = 5

更新树的信息【相当于填表】

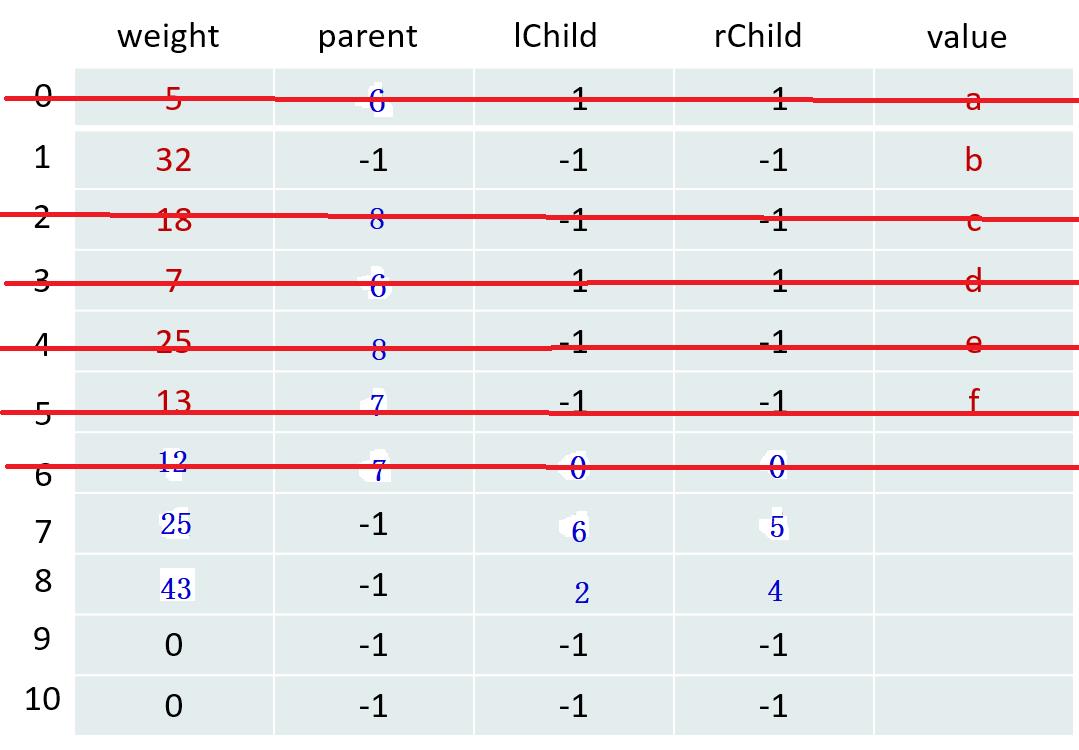
第3轮:

m1 = 18	m2 = 25
x1 = 2	x2 = 4

更新树的信息【相当于填表】

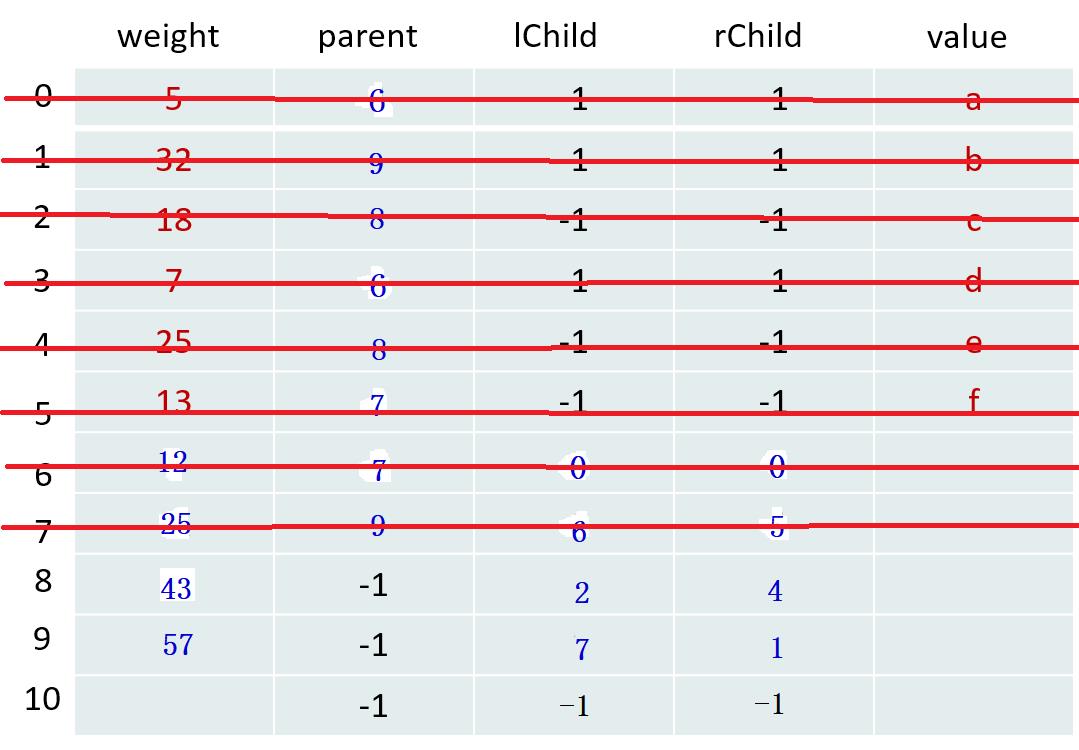
第4轮:

m1 = 25	m2 = 32
x1 = 7	x2 = 1

更新树的信息【相当于填表】

第5轮:

m1 = 43	m2 = 57
x1 = 8	x2 = 9

更新树的信息【相当于填表】

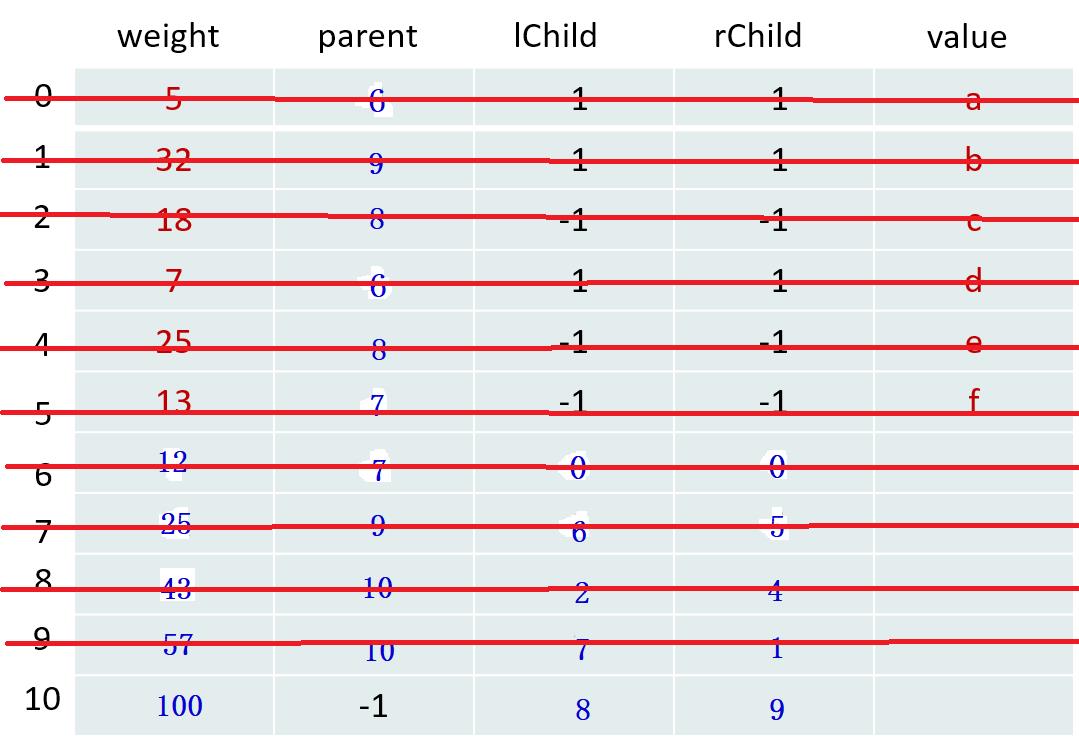
6片叶子需要合并5次

6. 构造完图示

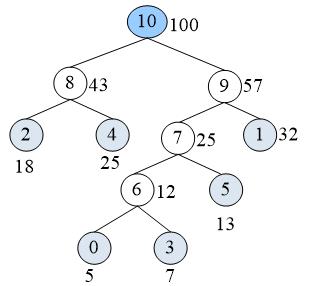
哈夫曼树编码

编码需从叶子结点出发走一条从叶子到根的路径

1. 编码结构体

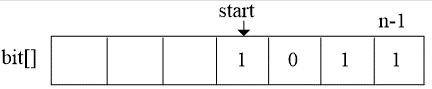
2. 编码结构体数组

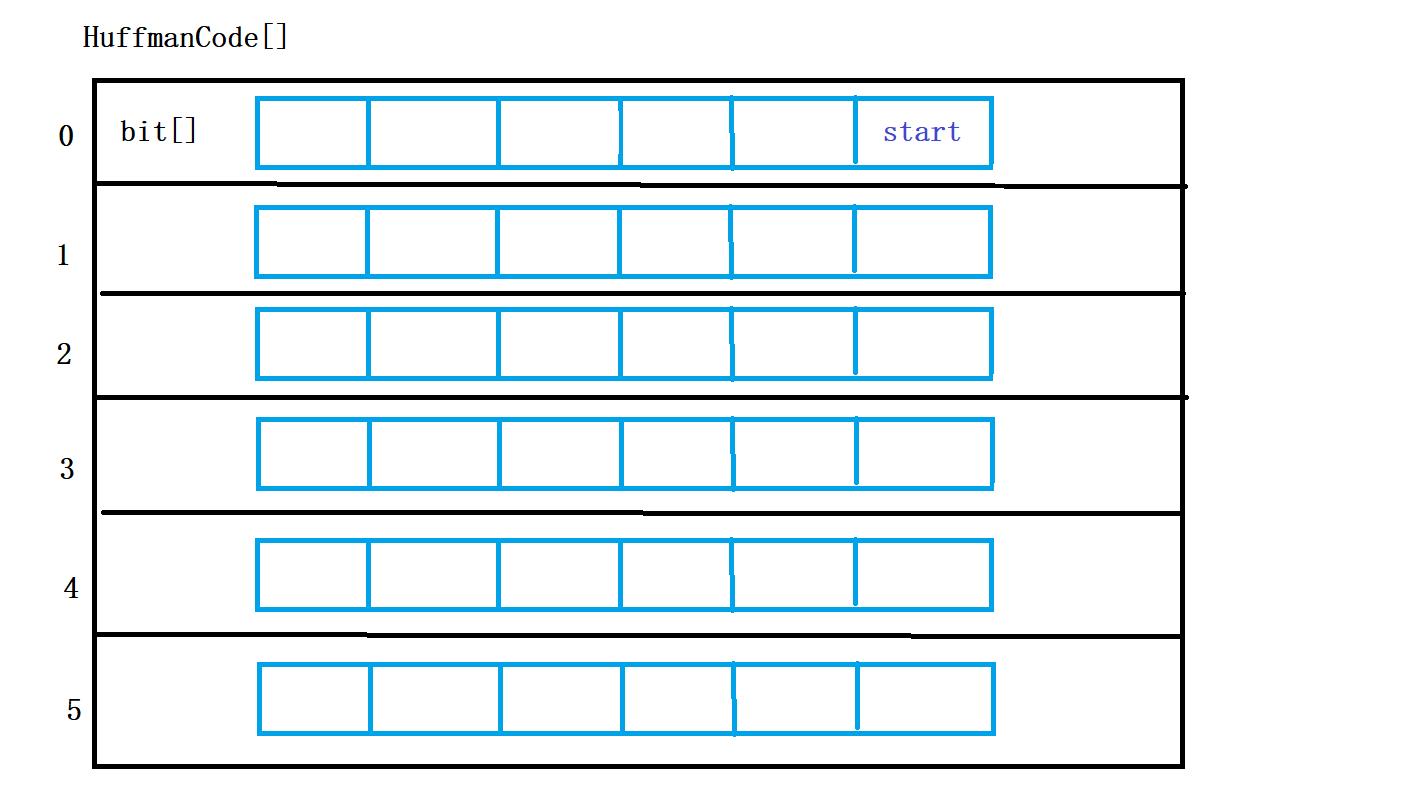
3. 对叶子结点进行编码

对n个叶子结点从后向前进行编码，不是树根就一直编码

左孩子编号为0

右孩子编号为1

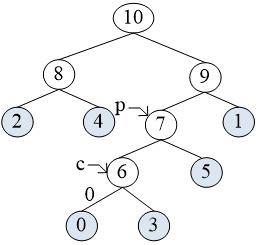
第一次for循环：完成下标为0的叶子的编码

start = 5
child = 0,   parent = 6

内部的while循环执行流程：

bit[5] = 0
start = 4
child = 6,   parent = 7

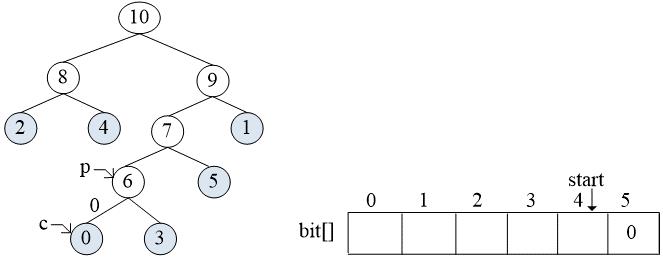
while循环：

bit[4] = 0
start = 3
child = 7,   parent = 9

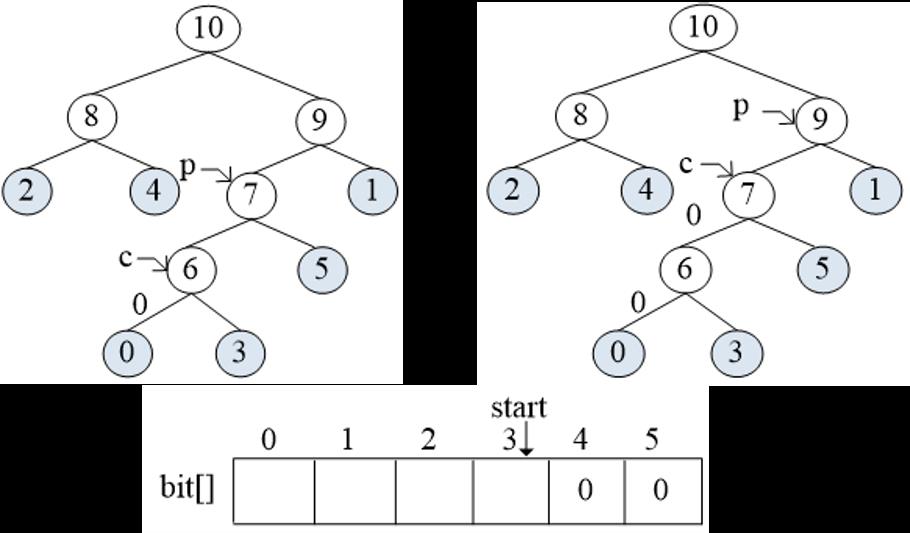
while循环：

bit[3] = 0
start = 2
child = 9,   parent = 10

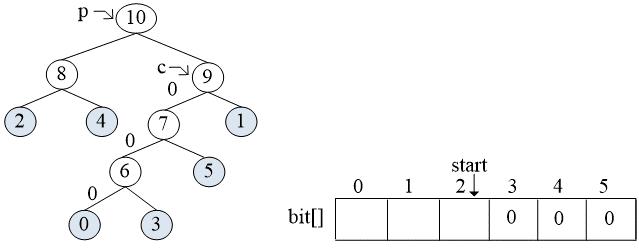
while循环：

bit[2] = 1
start = 1
child = 10,   parent = -1（结束）

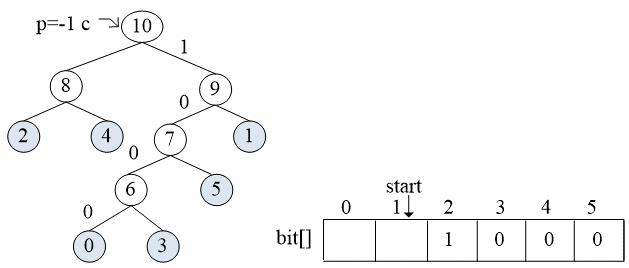
把叶子结点的编码信息从临时编码cd中复制出来，放入编码结构体数组

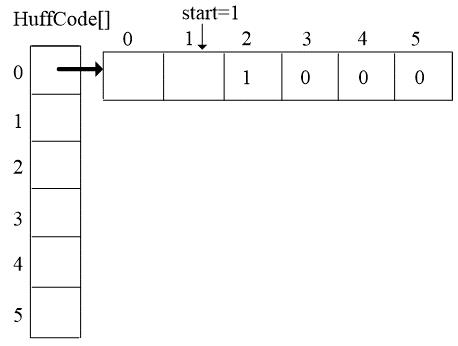
第二次for循环……

第三次for循环……

第四次for循环……

第五次for循环……

第六次for循环……

4. 编码后图示

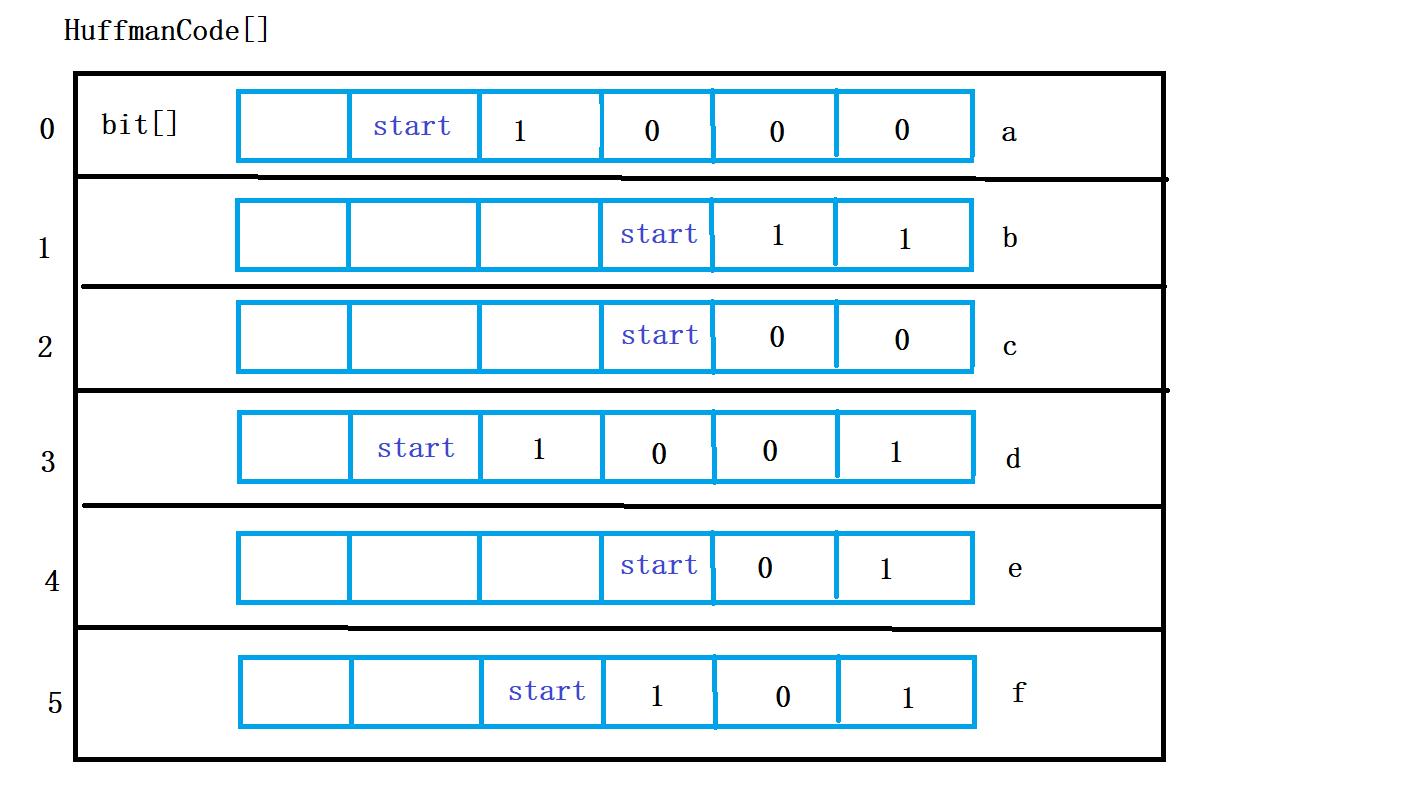
哈夫曼树译码

译码需要从根出发走一条从根到叶子的路径

1. 对叶子结点进行译码

对n个叶子结点从前向后进行译码，不是叶子就一直译码

第一次for循环：完成下标为0的叶子的译码

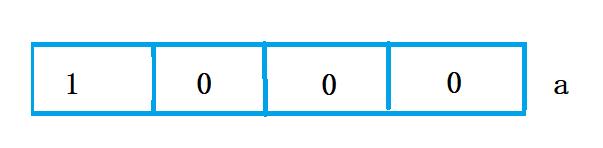
第二次for循环：完成下标为1的叶子的译码

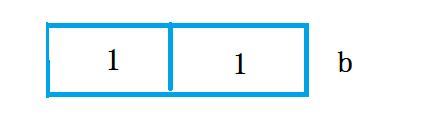
第三次for循环：完成下标为2的叶子的译码

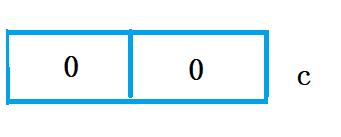
第四次for循环：完成下标为3的叶子的译码

第五次for循环：完成下标为4的叶子的译码

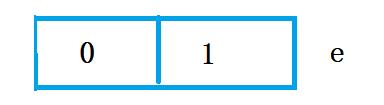
第六次for循环：完成下标为5的叶子的译码

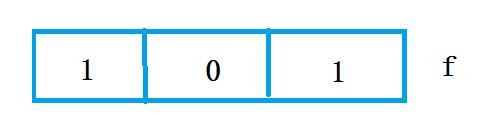
2. 最终运行结果