3. Distributional Reinforcement Learning with Quantile Regression

Posted 2020-12-21 hughcai

C51算法理论上用Wasserstein度量衡量两个累积分布函数间的距离证明了价值分布的可行性，但在实际算法中用KL散度对离散支持的概率进行拟合，不能作用于累积分布函数，不能保证Bellman更新收敛；且C51算法使用价值分布的若干个固定离散支持，通过调整它们的概率来构建价值分布。

而分位数回归(quantile regression)的distributional RL对此进行了改进。首先，使用了C51的“转置”，即固定若干个离散支持的均匀概率，调整离散支持的位置；引入分位数回归的思想，近似地实现了Wasserstein距离作为损失函数。

Quantile Distribution

假设(mathcal{Z}_Q)是分位数分布空间，可以将它的累积概率函数均匀分为(N)等分，即( au_0, au_1..., au_N( au_i=frac{i}{N},i=0,1,..,N))。使用模型( heta:mathcal{S} imes mathcal{A} o mathbb{R}^N)来预测分位数分布(Z_ heta in mathcal{Z}_Q)，即模型({ heta_i (s,a)})将状态-动作对((s,a))映射到均匀概率分布上。(Z_ heta (s,a))的定义如下

[Z_ heta (s,a):=frac{1}{N}sum_{i=1}^N delta_{ heta_i(s,a)} ag{1} ]

其中，(delta_z)表示在(zinmathbb{R})处的Dirac函数

与C51算法相比，这种做法的好处：

1. 不再受预设定的支持限制，当回报的变化范围很大时，预测更精确
2. 取消了C51的投影步骤，避免了一些先验知识
3. 使用分位数回归，可以近似最小化Wassertein损失，梯度下降不再有偏

Quantile Approximation

Quantile Projection

使用1-Wassertein距离对随机价值分布(Zin mathcal{Z})到(mathcal{Z}_Q)的投影进行量化：

[mathcal{Pi}_{W_1}Z:=underset{{Z_ heta}inmathcal{Z}_Q}{argmin}W_1(Z,Z_ heta) ]

假设(Z_ heta)的支持集为({ heta_1,..., heta_N })，那么

[W_1(Z,Z_ heta)=sum_{i=1}^N int_{ au_{i-1}}^{ au_i} |F_Z^{-1}(w)- heta_i|dw ]

其中，( au_i, au_{i-1}in[0,1])。论文指出，当(F_Z^{-1})是逆累积分布函数时，(F_Z^{-1}(( au_{i-1}+ au_i)/2))最小。因此，量化中点为(mathcal{hat au_i}=frac{ au_{i-1}+ au_i}{2}(1le ile N))，且最小化(W_1)的支持( heta_i=F_Z^{-1}(mathcal{hat au_i}))。如下图

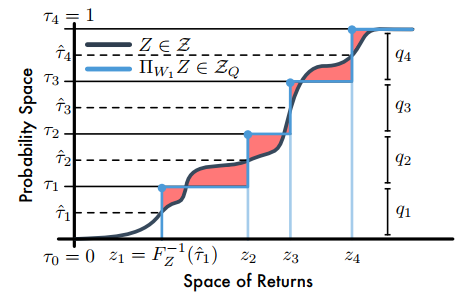
【注】C51是将回报空间(横轴)均分为若干个支持，然后求Bellman算子更新后回报落在每个支持上的概率，而分位数投影是将累积概率(纵轴)分为若干个支持(图中是4个支持)，然后求出对应每个支持的回报值；图中阴影部分的面积和就是1-Wasserstein误差。

Quantile Regression

建立分位数投影后，需要去近似分布的分位数函数，需要引入分位数回归损失。对于分布(Z)和一个给定的分位数( au)，分位数函数(F_Z^{-1}( au))的值可以通过最小化分位数回归损失得到

[mathcal{L}_{ ext{QR}}^ au( heta):=mathbb{E}_{hat Zsim Z}[ ho_ au (hat Z - heta)],quad ext{where} quad ho_ au (u)=u( au-delta_{{u<0}}),forall uinmathbb{R} ]

最终，整体的损失函数为

[sum_{i=1}^N mathbb{E}_{hat Zsim Z}[ ho_{hat{ au}_i} (hat Z - heta)] ]

但是，分位数回归损失在0处不平滑。论文进一步提出了quantile Huber loss：

[mathcal{L}_{mathcal{K}}(u)= egin{cases} & frac{1}{2}u^2,quadquadquadquad ext{if} |u|le mathcal{K} & mathcal{K}(|u|-frac{1}{2}mathcal{K}),,, ext{otherwise} end{cases} ]

[ ho_{ au}^{mathcal{K}}(u)=| au-delta_{{u<0}}|mathcal{L}_{mathcal{K}}(u) ]

Implement

QR TD-Learning

QRTD算法(quantile regression temporal difference learning algorithm)的更新

[ heta_i(s)leftarrow heta_i(s)+alpha (hat{mathcal{ au}}_i-delta_{{r+gamma z^prime < heta_i (s) }}) ]

(asimpi (cdot|s),rsim R(s,a),s^primesim P(cdot|s,a),z^primesim Z_ heta(s^prime))
其中，(Z_ heta)是由公式(1)给出的分位数分布，( heta_i (s))是状态(s)下(F_{Z^pi (s)}^{-1}(mathcal{hat au}_i))的估计值。

QR-DQN

QR-DQN算法伪代码

Append

1. Dirac Delta Function

[delta_a (x)=delta (x-a)=0,(x eq 0) quad且quad int_{-infty}^infty delta_a (x)d_x=1 ]

References

Will Dabney, Mark Rowland, Marc G. Bellemare, Rémi Munos. Distributional Reinforcement Learning with Quantile Regression. 2017.
Distributional RL