2. A Distributional Perspective on Reinforcement Learning

Posted 2020-12-21 hughcai

本文主要研究了分布式强化学习，利用价值分布(value distribution)的思想，求出回报(Z)的概率分布，从而取代期望值(即(Q)值)。

Q-Learning

Q-Learning的目标是近似Q函数，即在策略(pi)下回报(Z_t)的期望值：

[Q^{pi}(s,a)=mathbb{E}[Z_t|s,a] ]

Q-Learning的核心是Bellman方程。它可以通过时序差分学习迭代更新Q函数

[Q^{pi}(s,a)=r+gamma max_{a‘}Q(s‘,a‘) ag{1} ]

然后，最小化估计项(Q(s,a))和目标项(r+gamma max_{a^prime}Q(s^prime,a^prime))的均方误差损失

[L=mathbb{E}_{s,a,s^prime}igg(r+gamma max_{a^prime}Q(s^prime,a^prime)-Q(s,a)igg)^2 ag{2} ]

通过假设目标(r+gamma max_{a^prime}Q(s^prime,a^prime))为定量，最小化公式(2)使(Q(s,a))朝目标方向移动来优化网络。

Distributional RL

对于给定状态(s)和动作(a)，智能体获得的回报(Z(s,a))是服从某种分布的随机变量，传统的方法是利用它的期望值来优化策略。

而分布式强化学习的思想是直接作用在回报(Z(s,a))的价值分布上，而不是它的期望。

学习(Z(s,a))的概率分布，以此取代它的期望函数(Q(s,a))，有以下几个优势：

1. 学习到的概率分布所含信息比期望值要丰富。当两个动作期望值相同时，可以选择方差较小的动作
2. 针对一些稀疏奖励的场景，使用价值分布可以有效缓解
3. 只考虑期望值，可能会忽略在某一状态下回报显著的动作，导致学习陷入次优策略

Value Distribution

使用一个随机变量(Z(s,a))替代(Q(s,a))，(Z(s,a))用于表示回报的分布，被称为价值分布(value distribution)，它们的关系式为

[Q^pi(s,a)doteqmathbb{E}Z^pi(s,a)=mathbb{E}igg[sum_{t=0}^infty gamma^tR(s_t,a_t)igg]=sum_i p_i z_i ag{3} ]

(s_tsim P(cdot|s_{t-1},a_{t-1}),a_tsimpi(cdot|x_t),s_0=x,a_0=a)
同时，可以推出当前状态和下一状态的(Z)都服从同一分布(D)，因此，定义transition算子(mathcal{P}^pi)：

[P^pi Z(s,a):overset{D}=Z(s^prime,a^prime) ag{4} ]

(s^primesim P(cdot|s,a),a^primesim pi(cdot|s^prime))，(P^pi:Z o Z)

Policy Evaluation

根据公式(1)的Bellman方程，可以定义Bellman算子(mathcal{T}^pi)，如下

[mathcal{T}^pi Q(s,a)=mathbb{E}_{s^prime sim p(cdot |s,a),a^prime sim pi(cdot|s^prime)}ig[r+gamma Q(s^prime,a^prime)ig] ]

再结合公式(3)，可以推出Bellman方程的分布式版本

[mathcal{T}^pi Z(s,a):overset{D}=r+gamma Z(s^prime,a^prime) ag{5} ]

上式表示(Z(s,a))和(Z(s^prime,a^prime))都服从同一分布(D)。

衡量两个价值分布距离时，不光要考虑(Z)本身的随机性，还需要考虑输入自变量(s)和(a)。因此，该距离定义为：

[sup_{s,a} ext{dist}igg(r+gamma Z(s^prime,a^prime),Z(s,a)igg) ]

(s^prime sim p(cdot|s,a))
【注】上式式代替公式(2)来优化网络，但优化策略时仍然使用期望(Q(s,a))。论文用Wassertein metric作为距离度量，并证明了在该度量下，通过分布式Bellman方程更新，最终都能收敛于真实的价值分布，即Bellman算子(mathcal{T}^pi:Z o Z)可以看作(gamma)收缩：( ext{dist}(mathcal{T}Q_1,mathcal{T}Q_2)le gamma ext{dist}(Q_1,Q_2))，由于(Q^pi)是唯一不动点，即(mathcal{T}Q=QLeftrightarrow Q=Q^pi)，所以在不考虑近似误差的情况下，使(mathcal{T}^infty Q=Q^pi)。

Control

最优策略的定义是使回报期望最大的策略，因此，最优策略对应的价值分布也应是最优的。在只考虑期望的时候，最优策略是没有歧义的，也就是说，选择的最优价值函数只有一个，即唯一不动点(Q^pi)(Banach‘s Fixed Point Theorem)。但考虑价值分布时，会存在期望值相同的同等最优价值分布，因此存在一族不稳定的最优价值分布。论文中对所有最优策略排序，只允许存在一个最优策略，即可产生一个唯一不动点(Z^{pi^*})。

Implement

本文提出通过多个支持构建的离散分布表示价值分布，且(Z)和(Z‘)共享相同的离散支持集。这种离散分布的优点是表现力强(即它可以表示任何类型的分布，不限于高斯分布)。

此外，因为Wassertein距离作为度量难以实现，所以改用交叉熵损失优化网络。

实现原理：

1. 构建(Z(s^prime,a^prime))价值分布模型，将价值分布的区间([V_ ext{MIN},V_ ext{MAX}])分为N等分，每份间距为( riangle z=frac{V_ ext{MAX}-V_ ext{MIN}}{N-1})，得到一个离散支持的原子集({z_i=V_{ m MIN}+i riangle z,0le i<N })，图示如下

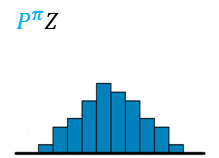
??然后，用参数化模型( heta:mathcal{S} imesmathcal{A} omathbb{R}^N)得到原子概率

[Z_ heta(s,a)=z_i quad ext{w.p.}quad p_i(s,a)doteq frac{e^{ heta_i}(s,a)}{sum_j e^{ heta_j}(s,a)} ]

2. 对(Z(s‘,a‘))先用(gamma)进行缩放，再用(R)进行位移，得到目标分布

[mathcal{T}^pi Z(s,a):overset{D}=R(s,a)+gamma P^pi Z(s,a) ag{6} ]

??图示如下

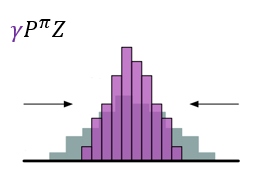
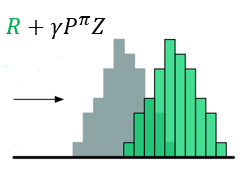
3. (gamma)是折扣回报，且奖励值不一定为( riangle z)的整数倍，所以不能保证通过Bellman算子更新所得的(Z(s^prime,a^prime))落在更新前相同值的原子上，因此，需要利用(Phi)投影。
   将样本Bellman更新(mathcal{hat T} Z_ heta)投影到(Z_ heta)的支持上，有效地将Bellman更新减少到多类别分类。给出采样转移((s,a,r,s^prime))，可以计算出每个原子(z_j)的Bellman更新(mathcal{hat T} z_jdoteq r+gamma z_j)，然后分配其概率(p_j(s^prime,pi(s^prime)))。因此，投影更新(Phi hat{mathcal{T}} Z_ heta(s,a))的第(i)个组成部分为

[(Phi mathcal{hat T} Z_ heta(s,a))_i=sum_{j=0}^{N-1}igg[1-frac{|[hat{mathcal{T}}z_j]^{V_{ m MAX}}_{V_{ m MIN}}-z_i|}{ riangle z} igg]_0^1 p_j(s^prime,pi(s^prime)) ]

??其中，([cdot]_a^b)将参数限制在范围([a,b])，(pi)是贪心策略。图示如下

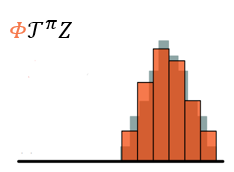
4. 使用KL散度来约束两个分布

[D_{KL}(Phi mathcal{hat T} Z_{widetilde{ heta}}(s,a)|Z_{ heta}(s,a)) ]

??最终，得到交叉熵损失函数

[mathcal{L}( heta)=-sum_im_ilog p_i(s_t,a_t; heta) ]

C51算法：

Append

1. Wasserstein Metric
它用于衡量概率分布的累积分布函数距离。(p)-Wasserstein度量(W_p(pin[1,infty]))可以看作是逆累积分布函数的(L^p)度量。假设两个分布为(U)和(V)，则(p)-Wasserstein距离为

[W_p(U,Y)=Big(int_0^1|F^{-1}_Y(mathcal{w})-F^{-1}_U(mathcal{w})|^pd_mathcal{w} Big)^{1/p} ]

对于随机变量(Y)，它的累积分布函数为(F_Y(y)=Pr(Yle y))，对应的逆累积分布函数为

[F_Y^{-1}(mathcal{w})=inf{yinmathbb{R}:mathcal{w}le F_Y(y)} ]

【注】对于(p=infty)，(W_infty(Y,U)=sup_{mathcal{w}in [0,1]|F^{-1}_Y(mathcal{w})-F^{-1}_U(mathcal{w})|})

2. KL散度与交叉熵损失
对于离散情况，(p)和(q)分布的KL散度为

[egin{aligned} D_{KL}(p||q) &=sum_{i=1}^N p(x_i)log frac{p(x_i)}{q(x_i)} &=sum_{i=1}^N p(x_i)[log p(x_i)-log q(x_i)] &=-sum_{i=1}^N p(x_i)log q(x_i) + sum_{i=1}^N p(x_i)log p(x_i)&=H(p,q)+H(p) end{aligned}]

References

Marc G. Bellemare, Will Dabney, Rémi Munos. A Distributional Perspective on Reinforcement Learning. 2017.
Distributional Bellman and the C51 Algorithm
Distributional RL