容斥原理 期望 莫比乌斯函数

Posted 2020-12-20 ilhyj

新章节 容斥原理

基本思路：根据给出的N一般很小的原理，我们需要明确三个事情

集合是什么，条件是什么，什么满足什么不满足

然后通过二进制状态压缩的方式枚举每一个变量的存在与否

根据奇偶性对答案+或者-就可以统计出原来的答案

一般来说，其中会有很明显的集合重叠特征

t1牛皮的鲜花

• 发现n很小，但是每一个集合都有限制
• 考虑去掉一部分条件（解题法）
• 如果没有限制的话
• 知识点，不定方程 Σxi=M（xi>=0）
• 令yi=xi+1，那么转化为 Σ y=M+N （yi>=1） 这个时候可以用隔板法解决
• 答案为C(n-1,n+m+1)
• 然后考虑加上限制，直接求不好求，我们求不合法的方案数
• 如何不合法 （xi<=ai） 那么我们直接先取出(ai+1）只花就一定不满足条件i
• 根据容斥原理，奇数减偶数加就可
• C(N-1,N-M+1-(A[J]+1）
• 考虑优化的第一个思路：避免冗余计算
• 计算组合数的第一个办法:定义法：因为M很大，没有办法打表，但是发现N很小，根据组合数的性质计算一个组合数的时间不超过N
• 所以可以之间使用定义计算
• 除法要取模：我们使用逆元
• 观察到：每次我们的分母都是一样的，所以只需要计算一次就好
• 具体细节见代码：

• #include <stdio.h>
  #include <algorithm>
  #include <cstring>
  
  using namespace std;
  
  typedef long long ll;
  ll a[30];
  ll n,m;
  int down=1;
  const int q=1e9+7;
  
  int ksm(int a,int k,int q)
  {
      ll temp=1;
      while(k)
      {
          if(k&1) temp=(ll)temp*a%q;//开ll防爆 
          a=(ll)a*a%q;
          k>>=1;
      }
      return temp;
  }
  ll C(ll a,ll b)
  {
      if(a<b) return 0;//C(A,B)=0
      ll up=1;
      for(ll i=a;i>a-b;i--) up=(ll)i%q*up%q;//这里要先把imod了，因为i是ll，再乘就爆炸 
      return up*down%q;
  }
  int main()
  {
      scanf("%lld%lld",&n,&m);
      for(int i=0;i<n;i++) scanf("%lld",&a[i]);
      for(int i=1;i<=n-1;i++) down=(ll)down*i%q;
      down=ksm(down,q-2,q);//费马小定理，使用于mod数是质数 
      int res=0;
      for(int i=0;i<(1<<n);i++)
      {
          ll A=n+m-1,B=n-1;//每次定义一个变量；他有什么计算而来，要计算什么，会不会爆炸 
          int sign=1;
          for(int j=0;j<n;j++)
          {
              if(i>>j&1)
              {
                  A-=a[j]+1;
                  sign*=-1;//容斥原理 
              }
          }
          res=(ll)(res+C(A,B)*sign)%q;//每次modq，防止爆ll 
      }
      printf("%d",(res+q)%q);//变成正整数 
      return 0;
  }

  int 10e9 ll 1e18

• 莫比乌斯函数：
• 质因数分解：pI^ai
• ai>1 0 指数和偶数：1 指数和奇数 -1
• 问题抽象：求1-n中和n互质的数的个数 欧拉函数：
• 代码：

• void getmu(int maxx)
  {
      mu[1]=1;
      for(int i=2;i<=maxx;i++)
      {
          if(!vis[i])
          {
              prime[cnt++]=i;
              mu[i]=-1;
          }
          for(int j=0;j<cnt,i*prime[j]<=maxx;j++)
          {
              vis[i*prime[j]]=1;
              if(i%prime[j]==0) break;
              else mu[i*prime[j]]=-mu[i];//指数的奇偶性改变
          }
      }

   

• 6.除数函数
  1.表示n的因子的k次方之和 Σ(d|n) d^k 表示对n的所有约数求和
  2.k=0 时是约数个数 成为 d(n) k=1 的时候记为 bulabula(n)
  除数函数都是积性函数：
  约数个数：分解后为 （1+a1)*)(1+a2)... 各个素因子的贡献独立

  7.欧拉函数 φ(n)表示 1-n 和 n互质的正整数的个数
  1.由n的分解，加上容斥原理来求解
  φ(n)=n - n/p1 -n / p2 .... 容斥原理（剪多了
  =n(1-1/p1)(1-1/p2)...
  =(p1^a1-1(p1-1))*(p2^a-1(p2-1))..
  也就是每个质因子要单独考虑 独立性 所以是积性函数
  【积性函数都有独立性】
  2.n=Σ(d|n) φ（n);

  证明 （n,i)=d, 那么（n/d,i/d)=1 i/d<=n/d 所以这样的i一共有φ(n/d)个
  所以考虑所有的d|n 也就考虑了 1-n 的所有整数
  由此 n=Σ(d|n)φ（n/d) 要注意 d和n/d 再某种意义上遍历过程是等价的，只不过是顺序相反而已
  以6为例

引入新的函数 g(x)

 

 

 

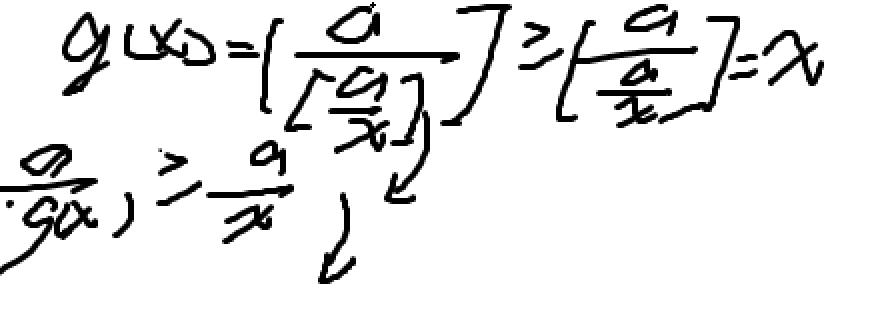
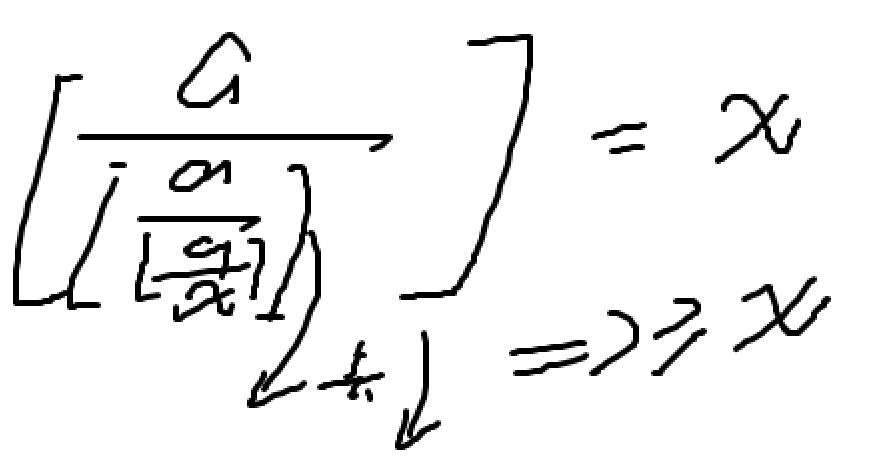
 所以说 [a/g(x)]>=[a/x]并且[a/g（x）]<=[a/x]所以说两者相等

再证明第二个定义：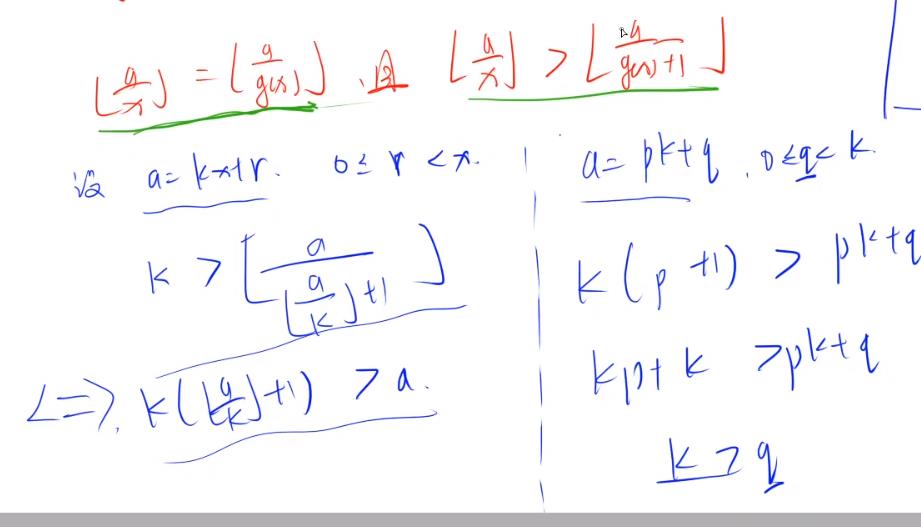

 

 结论2：[a/i]中一共最多有2根号a个不同的值，可以分块跳

#include <stdio.h>
#include <algorithm>
#include <cstring>

using namespace std;

typedef long long ll;
const int maxn=50020;

bool st[maxn];
int prime[maxn],mob[maxn],sum[maxn];
int cnt;

void init(int n)
{
    mob[1]=1;
    for(int i=2;i<=n;i++)
    {
        if(!st[i])
        {
            prime[cnt++]=i;
            mob[i]=-1;
        }
        for(int j=0;j<cnt,i*prime[j]<=n;j++)
        {
            int t=prime[j]*i;
            st[t]=true;
            if(i%prime[j]==0) break;
            mob[t]=-mob[i];
        }
    }
    for(int i=1;i<=n;i++) sum[i]=sum[i-1]+mob[i];//因为是单独计算每一段的贡献，所以需要对mob做一个前缀和
}
int main()
{
    init(50000);
    //for(int i=1;i<=30;i++) printf("%d ",mob[i]);
    int T;
    scanf("%d",&T);
    while(T--)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        a/=c;b/=c;
        ll res=0;
        int n=min(a,b);
        for(int l=1,r;l<=n;l=r+1)
        {
            r=min(n,min(a/(a/l),b/(b/l)));
            res+=(ll)(sum[r]-sum[l-1])*(a/l)*(b/l);
        }
        printf("%lld
",res);
    }
    return 0;
}
 

 #莫比乌斯函数相关网站：https://www.cnblogs.com/peng-ym/p/8647856.html

对于狄利克雷卷积我们再进行一下复习:

8.dieichlet 狄利克雷卷积
1.设f,g是数论函数 h(n)=Σ(d|n)f(d)g(n/d)
h = f * g;【是函数一卷卷出来另一个函数，也就是两个函数的值】
2.单位函数是狄利克雷卷积的单位元 也就是 e*f=f*e=f 
3.满足交换律和结合律 （d和n/d的相对性）
证明结合律：考虑求和变换顺序
4.若f，g都是积性函数 则f*g也是积性函数【保持了元素因子独立的特性】
5.许多关系可以用卷积来表示 1表示为1的常函数
6.idk（n)=n^k,id1=id(n的取值就是n）
7.除数函数：西格玛k=1*idk 
8.欧拉函数 id=φ*1

然后，来到莫比乌斯变化：

1.莫比乌斯函数的两个性质

 

 2.关于莫比乌斯反演的证明

 

首先：我们需要对求和符号进行说明（文章：https://blog.csdn.net/a574780196/article/details/82932986?utm_medium=distribute.pc_aggpage_search_result.none-task-blog-2~all~first_rank_v2~rank_v25-7-82932986.nonecase&utm_term=%E6%B1%82%E5%92%8C%E7%AC%A6%E5%8F%B7%E8%BF%90%E7%AE%97%E6%B3%95%E5%88%99&spm=1000.2123.3001.4430）

首先需要关注的是求和符号的三个性质 ：结合律，分配率，函数律

2.二级求和符号需要前后两者等价，一般是可以将其中一种东西当做常量来求

3.非常重要的一点就是：如果说在高一级的求和符号中使用了某种变量来约束下标的话，那么之后一定要用其他的字母来作为循环变量

证明如下：

 

 关注求和的顺序改变：前面一个是对于每一个d，i求和，下面一个就是对于每一个i，d求和，两者是相乘的性质，分配率显然满足

由此我们可以得到莫比乌斯反演的两种形式：

 

 

 

 专题二：期望和概率

• 即期望可以通过子事件的发生期望乘以概率来求，这就是可以用dp来做的基础
• 期望问题的一般性质：起点唯一，终点不唯一
• 那么我们可以也就是定义状态到终点的期望：f(n)=0,求解f(1）
• 本质上就是要求解一个递归关系，也就是一个dp
• 那么计算一个状态时只要保证前面的状态都被计算完（简单的记忆化搜索实现）了就好
• 那么我们要考虑爆栈的问题（现在不用了）
• 本题的本质就是寻找递推式，然后根据题目之间的依赖关系求解求解

• #include <stdio.h>
  #include <algorithm>
  #include <cstring>
  
  using namespace std;
  
  const int maxn=3e5+20;
  
  int head[maxn],nex[maxn],ver[maxn],wei[maxn],tot;
  int n,m;
  double f[maxn];
  int dout[maxn];
  
  void add(int x,int y,int z)
  {
      ver[++tot]=y;
      wei[tot]=z;
      nex[tot]=head[x];
      head[x]=tot;
  }
  double dp(int x)
  {
      if(f[x]>=0) return x;
      if(x==n) return 0;
      f[x]=0;
      for(int i=head[x];i;i=nex[i])
      {
          int y=ver[i];
          f[x]+=(wei[i]+f[y])/dout[x];//推导出来的递推式
      }
      return f[x];
  }
  int main()
  {
      scanf("%d%d",&n,&m);
      for(int i=1;i<=m;i++)
      {
          int a,b,c;
          scanf("%d%d%d",&a,&b,&c);
          add(a,b,c);
          dout[a]++;//
      }
      memset(f,-1,sizeof(f));//记忆化搜索记住要初始化成“not number”
      printf("%.2f",dp(1));
      return 0;
  }

  对于空间复杂度计算的补充：

• 32位系统下，int、long、long long、__int64所占字节数和取值范围
  字节数
  char: 1字节（8位）
  int: 4字节 (32位，取值范围 -2^31 ～ 2^31-1)
  unsigned int : 4字节 (32位，取值范围 0 ～ 2^32-1)
  long: 4字节 (32位，取值范围 -2^31 ～ 2^31-1)
  unsigned long : 4字节 (32位，取值范围 0 ～ 2^32-1)
  long long : 8字节(64位，取值范围 -2^63 ～ 2^63-1)
  取值范围
  int   :   -2147483648 ～ 2147483647 
  unsigned  int  :    0 ～ 4294967295   
  long   :  -2147483648 ～ 2147483647
  unsigned long  :  0 ～ 4294967295
  long long   :  -9223372036854775808 ～ 9223372036854775807
  unsigned long long  :  0 ～ 1844674407370955161

  __int64  :  -9223372036854775808 ～ 9223372036854775807
  unsigned __int64  :  0 ～ 1844674407370955161

• 也就数数组大小*字节数/1024/1024的出来的单位是MB就可以比较了
• 在多维的数组空间判断终有用

T2：扑克牌

• 经过两道水题（bushi）的洗礼，我们大概知道了到底应该怎么做期望：
• 期望的本质仍旧是dp，只不过初始量是终点状态为0；
• 我们需要寻找：状态的表示，状态的转移（转移过程一定要注意判断越界），记忆化搜索的实现
• 同时，我们还需要判断期望过大的情况：也就是E>INF/2，（INF=1E20）,同时期望过小也是一个道理;
• 用终点状态来想表示f（a,b,c,d,x,y）；来表示四张牌以及两张特殊牌的表达方式
• 剩下就是一下细节，见代码就好：

#include <stdio.h>
#include <algorithm>
#include <cstring>

using namespace std;

const int N=15;
const double INF=1e20;
double f[N][N][N][N][5][5];
int A,B,C,D;

double dp(int a,int b,int c,int d,int x,int y)
{
    double &v=f[a][b][c][d][x][y];
    if(a>13||b>13||c>13||d>13) return INF;
    if(v>=0) return v;
    int as=a+(x==0)+(y==0);
    int bs=b+(x==1)+(y==1);
    int cs=c+(x==2)+(y==2);
    int ds=d+(x==3)+(y==3);
    if(as>=A&&bs>=B&&cs>=C&&ds>=D) return v=0;//达到了终点状态
    int sum=a+b+c+d+(x!=4)+(y!=4);
    sum=54-sum;//计算概率
    if(sum<=0) return v=INF;//判断是否越界，这里统一用INF表示不存在的数
    v=1;
    if(a<13) v+=(13.0-a)/sum*dp(a+1,b,c,d,x,y);
    if(b<13) v+=(13.0-b)/sum*dp(a,b+1,c,d,x,y);
    if(c<13) v+=(13.0-c)/sum*dp(a,b,c+1,d,x,y);
    if(d<13) v+=(13.0-d)/sum*dp(a,b,c,d+1,x,y);
    if(x==4)
    {
        double t=INF;
        for(int i=0;i<=3;i++) t=min(t,1.0/sum*dp(a,b,c,d,i,y));//注意要写上dp函数
        v+=t;
    }
    if(y==4)
    {
        double t=INF;
        for(int i=0;i<=3;i++) t=min(t,1.0/sum*dp(a,b,c,d,x,i));
        v+=t;
    }
    return v;
    
}
int main()
{
    scanf("%d%d%d%d",&A,&B,&C,&D);
    memset(f,-1,sizeof(f));
    double t=dp(0,0,0,0,4,4);
    if(t>INF/2) t=-1;//判断越界
    printf("%.3lf",t);
    return 0;
}