学军联赛模拟 第十八测 题解

Posted 2020-12-20 evenbao

(A.)

首先有个朴素的动态规划思路 ， 记 (f_{i , j}) 表示前 (i) 个位置 ， 最后一个位置的颜色是 (j) 的方案数。

转移要用到容斥原理 ， 用总方案数减去 (j) 连续出现 (a_{j} + 1) 次的方案数。 记 (g_{i} = sum{f_{i , j}})。 则 (f_{i , j} = g_{i - 1} - (g_{i - a_{j} - 1} - f_{i - a_{j} - 1 , j}))。

注意到对于 (a_{j}) 相同的颜色显然状态相同 ， 可以分批转移。 时间复杂度 : (O(N ^ 2))

(B.)

二分答案 ， 将每个数减去 (x) ， 那么要求的转化为序列中总和大于 (0) 的区间个数。

这个问题可以用树状数组等数据结构求解二维偏序得到。

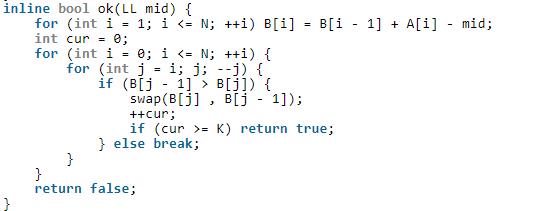
但事实上可以不用数据结构 ， 因为插入排序的时间复杂度是 (O(逆序对个数)) ， 所以可以直接运行插入排序 ， 如果超过 (K) 次交换操作就直接返回。

这样的时间复杂度是 (O(NlogN)) 的。

附核心代码 ：

(C.)

记 (dp_{i , j}) 表示考虑了前 (i) 个字符串 ， 一个拼合串的后缀为 (s_{i}) , 另一个为 (s_{j}) 的最短长度。

考虑优化 ， 不妨将字符串记进状态 ， 记 (dp_{i , s}) 表示前 (i) 个字符串 ， 有一个串后缀为 (s_{i}) ， 另一个有一个后缀是 (s) 的最短长度。

不妨建立字典树存储状态。

这样就有两种状态 ：

第一种 ， 接在上一个串后面 ， 这样相当于给所有的状态加上一个数 ， 可以直接在字典树上打标记。

第二种 ， 和某一个串"缩"起来 ， 这样可以在字典树上取 (min) 得到 ， 对于这种情况 ， 还需枚举当前串的一个后缀更新树上的节点。

时间复杂度 : (O(NM))