排序专项训练

Posted 2023-02-25 清浅岁月

排序专项训练

排序算法概括:

排序算法：

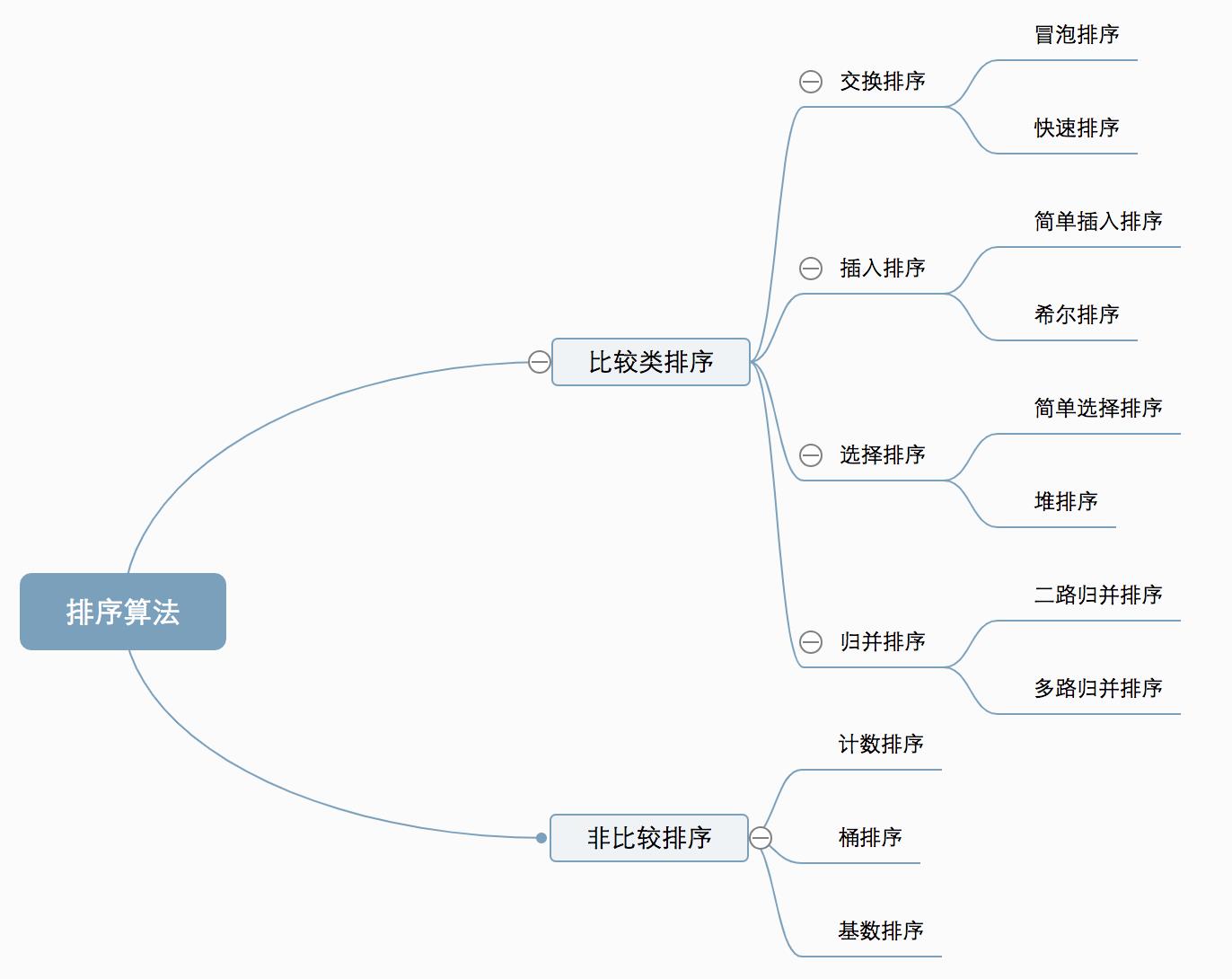
算发复杂度：

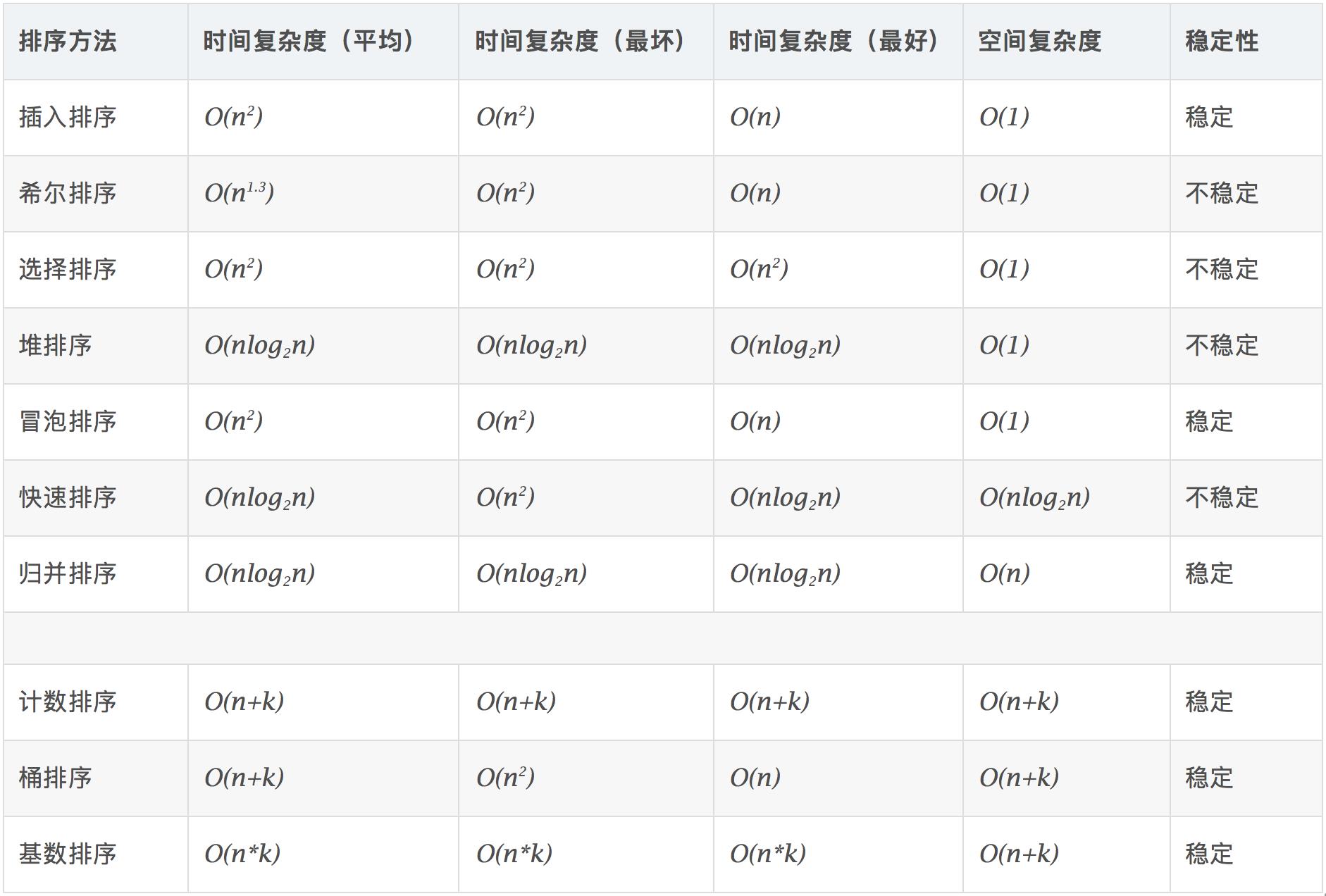
冒泡

 /***
     * 冒泡排序  时间复杂度o(n的平方)   空间复杂度
     * @param num
     * @return
     */
    public int[] bubbleSort(int[] num) 
        if (num == null || num.length < 2) 
            return num;
        
        int length = num.length;
        for (int i = 0; i < length - 1; i++) 

            for (int j = 0; j < length - i - 1; j++) 
                if (num[j] > num[j + 1]) 
                    int temp = num[j];
                    num[j] = num[j + 1];
                    num[j = 1] = temp;
                
            
        

        return num;
    

选择

    /**
     * 选择排序 时间复杂度：o(n的平方)，空间复杂度o(1)
     *
     * @return
     */
    public int[] selectSort(int[] num) 
        if (num == null || num.length < 2) 
            return num;
        
        int len = num.length;
        for (int i = 0; i < len - 1; i++) 
            int min = i;
            // 找见最小的数据的下标
            for (int j = 1; j < len; j++) 
                if (num[min] > num[j]) 
                    min = j;
                
            
            // 与第一个元素交换，第一个元素为最小
            int temp = num[i];
            num[i] = num[min];
            num[min] = temp;
        

        return num;
    

插入

    /**
     * 插入排序
     * 时间复杂度 o(n的平方)   空间复杂度o(1)
     *
     * @param num
     * @return
     */
    public int[] insertSort(int[] num) 
        if (num == null || num.length < 2) 
            return num;
        
        int len = num.length;
        for (int i = 1; i < len; i++) 
            int pre = i - 1;
            int temp = num[i];  
            
            // 从后往前遍历，依次往后放
            while (pre >= 0 && num[pre] > temp) 
                num[pre + 1] = num[pre]; 
                pre--;
            
            //将拿出的元素放到腾出来的位置
            num[pre + 1] = temp;
        
        return num;
    

希尔

 /***
     * 作为插入排序的优化使得
     * 希尔排序时间复杂度 o(nlogn) 空间复杂度0(1)
     *  特点 for——for-while   两个for+1个while
     * @return
     */
    public int[] shellSort(int[] num) 
        if (num == null || num.length < 2) 
            return num;
        

        int length = num.length;
        // 决定分几次组
        for (int gap = length / 2; gap > 0; gap = gap / 2) 

            // 再使用插入排序进行排序
            for (int i = gap; i < length; i++) 
                int pre = i;
                int temp = num[i];
                while (pre - gap >= 0 && num[pre - gap] > temp) 
                    num[pre] = num[pre - gap];
                    pre = pre - gap;
                
                num[pre] = temp;
            
        
        return num;
    

快排

普通排序

 /***
     * 快速排序
     * 选择一个中轴元素，中轴元素的左边是小数，右边是大数
     *时间复杂度：最好(nlogn） 最坏 o(n的平方)
     */
    public void quickSort(int[] num, int left, int right) 

        if (right > left) 
            // 中轴元素分为
            int mid = sort(num, left, right);
            quickSort(num, left, mid-1);
            quickSort(num, mid + 1, num.length);
        

    

    private int sort(int[] num, int left, int right) 
        int i = left + 1;
        int j = right;
        int povit = num[left];
        while (true) 

            while (i < j && num[i] <= povit) 
                i++;
            
            while (i < j && num[j] >= povit) 
                j--;
            
            if (i > j) 
                break;
            
            int temp = num[i];
            num[i] = num[j];
            num[j] = temp;
        
        num[left] = num[j];
        num[j] = povit;
        return j;
    

优化过的：

随机获取中轴元素，不再拿第一个作为中轴元素，不存在最坏情况

   /***
     * 快速排序
     * 选择一个中轴元素，中轴元素的左边是小数，右边是大数
     *时间复杂度：最好(nlogn） 最坏 o(n的平方)
     */
    public void quickSort(int[] num, int left, int right) 

        if (right > left) 
            // 中轴元素分为
            int mid = randomSort(num, left, right);
            quickSort(num, left, mid-1);
            quickSort(num, mid + 1, num.length);
        

    

    private int sort(int[] num, int left, int right) 
        int i = left + 1;
        int j = right;
        int povit = num[left];
        while (true) 

            while (i < j && num[i] <= povit) 
                i++;
            
            while (i < j && num[j] >= povit) 
                j--;
            
            if (i > j) 
                break;
            
            int temp = num[i];
            num[i] = num[j];
            num[j] = temp;
        
        num[left] = num[j];
        num[j] = povit;
        return j;
    

// 随机获取
    private int random(int min, int max) 
        Random random = new Random();
        int m = random.nextInt(max) % (max - min + 1) + min;
        return m;
    

// 交换第一个与随机获取的那个元素位置

    private void swap(int[] num, int random, int left) 
        int temp = num[left];
        num[left] = num[random];
        num[random] = temp;
    

    /**
     * 优化版本
     * 有可能存在比中轴元素都大，或者都小的情况，
     * 放置出现中轴元素的获取随机获取
     *
     * @param num
     * @param left
     * @param right
     * @return
     */
    private int randomSort(int num[], int left, int right) 
        int rn = random(left, right);
        swap(num, rn, left);
        return sort(num, left, right);
    
    
    

归并

/***
     * 归并排序的思想
     *
     * 时间复杂度 o(nlognO)
     * )
     * 分而治之的
     *
     * 拆封为最小单元，并需要额外的一个数组来缓存数据
     *
     * 递归
     *
     */
    public void mergeSort(int[] num, int left, int right) 

        int mid = (left + right) / 2;
        // 拆
        mergeSort(num, left, mid);
        mergeSort(num, mid , right);
        // 合
        merge(num, left, mid + 1, right);

    

    private void merge(int[] num, int left, int mid, int right) 
        int[] arrayTemp = new int[num.length];

        int rightstart = mid + 1;
        int third = 0;
        int temp = left;

        // 将两个数组长度一样的先比较后放如缓存数组
        while (left < mid && rightstart < right) 
            if (num[left] < num[rightstart]) 
                arrayTemp[third++] = num[rightstart++];
             else 
                arrayTemp[third++] = num[left++];
            
        
        // 左边数组剩余的元素
        while (left < mid) 
            arrayTemp[third++] = num[left++];
        

        //右边数组剩余的元素
        while (mid < right) 
            arrayTemp[third++] = num[right++];
        

        // 最后将缓存数组中的数据放入到原数组
        while (temp < right) 
            num[temp] = arrayTemp[temp++];
        

    

排序相关的题目

无序数组，返回排序后 相邻数据的最大差值

解法一：排序后+相邻元素做差 时间复杂度依赖于排序的时间复杂度+相邻做差的n次既：o(排序的时间复杂度+n)

解法二：使用计数排序 时间复杂度为O（n+k），空间复杂度同样是O（n+k）

  /***
     * 无序数组返回    排序后相邻数据，返回最大差值
     * @param nums  8.6.1.7.9   相邻最大差值 5
     * @return
     * 1.排序+做差      时间复杂度 o(n平方)+n
     * 2.快排归并希尔    时间复杂度o(nlogn+n)
     * 3.计数排序       时间复杂度 o(n+k)  空间复杂度o(n+k) 使用与数据相对均衡，最大与最小值差值较小的情况
     * 4.桶排序         时间复杂度 o(n)   空间复杂度o(n) 
     *
     *
     */
    public int getMaxAdjustDifference(int[] nums) 
        int max = nums[0];
        int min = nums[0];

        // 寻找最小值与最大值，创建数组
        for (int i = 1; i < nums.length; i++) 
            if (nums[i] > max) 
                max = nums[i];
            
            if (nums[i] < min) 
                min = nums[i];
            
        

        int arrayLength = max - min + 1;

        int[] tempArray = new int[arrayLength];

        // 将计数数据填充到数组中
        for (int i = 0; i < nums.length; i++) 
            tempArray[nums[i] - min]++;
        

        // 获取相邻连续的为零的个数，个数下标互减
        int count = 0;
        //开始为0的下标
        int startindex = 0;
        //结束为0的下标
        int endindex = 0;
        // 为0的最大数 ，动态更新
        int maxCount = 0;


        for (int i = 0; i < tempArray.length; i++) 
            if (tempArray[i] == 0) 
                if (count == 0) 
                    startindex = i - 1;
                
                count++;
             else 
                count = 0;
            

            if (count >= maxCount) 
                maxCount = count;
                endindex = i + 1;
            
        

        // 下标的差值即为最大差值
        // 造成最大差值的舒数是min+endindex
        // 造成最大差值的舒数是min+startindex

        return endindex - startindex;

解法三：使用桶排序

    public int getMaxAdjustDifference(int[] nums) 
    
        int max = nums[0];
        int min = nums[0];

        // 寻找最小值与最大值，创建桶
        for (int i = 1; i < nums.length; i++) 
            if (nums[i] > max) 
                max = nums[i];
            
            if (nums[i] < min) 
                min = nums[i];
            
        

        // 桶的个数
        int bucketNum = nums.length;

        Bucket[] bukets = new Bucket[bucketNum];

        for (int i = 0; i < bucketNum; i++) 
            bukets[i] = new Bucket();
        


        // 桶的容量范围
        int distance = max - min;


        // 将原始数据封装到桶中，桶中只存对应范围的最大值最小值

        for (int i = 0; i < nums.length; i++) 
            int index = ((nums[i] - min) * (bucketNum - 1)) / distance;
           if (bukets[index].max == null || bukets[index].max < nums[i]) 
                bukets[index].max = nums[i];
            
            if (bukets[index].min == null || bukets[index].min > nums[i]) 
                bukets[index].min = nums[i];
            
        


        // 遍历桶，获取后一个桶的最小值值与前一个桶的最大值做差，即可获取相邻最大查值
        int bucketsmax = 0;
        int leftmax = bukets[0].max;

        for (int i = 1; i < bukets.length; i++) 

            if (bukets[i].min - leftmax > bucketsmax) 
                bucketsmax = bukets[i].min - leftmax;
            
            leftmax = bukets[i].max;

        
        return bucketsmax;

    
    
    class Bucket 
        Integer max;
        Integer min;