数据结构-八种排序算法

Posted 2020-12-20 lgh544

一、常见的排序算法分类

 

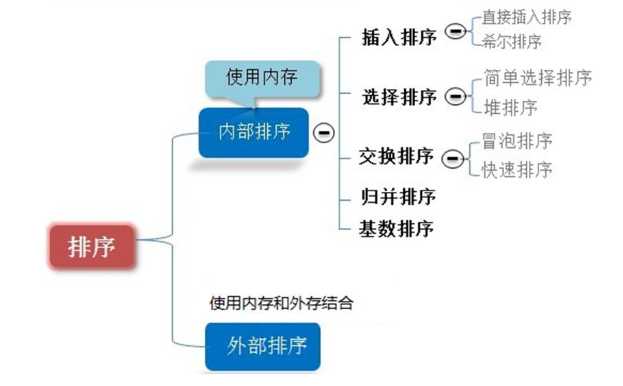
二、各种算法的时间复杂度

 

 

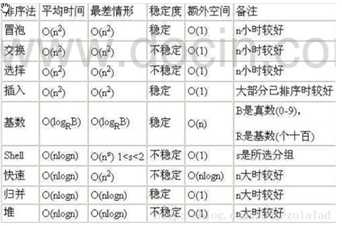
 三、冒泡排序

　　冒泡排序（BubbleSorting）的基本思想是：通过对待排序序列从前向后（从下标较小的元素开始）,依次比较相邻元素的值，若发现逆序则交换，使值较大的元素逐渐从前移向后部，就象水底下的气泡一样逐渐向上冒。

 

 

 小结上面的图解过程:

(1)一共进行数组的大小-1次大的循环

(2)每一趟排序的次数在逐渐的减少

(3)如果我们发现在某趟排序中，没有发生一次交换，可以提前结束冒泡排序。这个就是优化

 

 

public class BubbleSort {

    public static void main(String[] args) {
                int arr[] = {3, 9, -1, 10, 20};
        
        System.out.println("排序前");
        System.out.println(Arrays.toString(arr));        
                bubbleSort(arr);
                System.out.println("排序后");
        System.out.println(Arrays.toString(arr));
        }
        public static void bubbleSort(int[] arr) {
        // 冒泡排序 的时间复杂度 O(n^2), 自己写出
        int temp = 0; // 临时变量
        boolean flag = false; // 标识变量，表示是否进行过交换
        for (int i = 0; i < arr.length - 1; i++) {

            for (int j = 0; j < arr.length - 1 - i; j++) {
                // 如果前面的数比后面的数大，则交换
                if (arr[j] > arr[j + 1]) {
                    flag = true;
                    temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                }
            }
            //System.out.println("第" + (i + 1) + "趟排序后的数组");
            //System.out.println(Arrays.toString(arr));

            if (!flag) { // 在一趟排序中，一次交换都没有发生过
                break;
            } else {
                flag = false; // 重置flag!!!, 进行下次判断
            }
        }
    }

}
    

四、选择排序

选择排序（selectsorting）也是一种简单的排序方法。它的基本思想是：第一次从arr[0]~arr[n-1]中选取最小值，与arr[0]交换，第二次从arr[1]~arr[n-1]中选取最小值，与arr[1]交换，第三次从arr[2]~arr[n-1]中选取最小值，与arr[2]交换，...，第i次从arr[i-1]~arr[n-1]中选取最小值，与arr[i-1]交换，...,第n-1次从arr[n-2]~arr[n-1]中选取最小值，与arr[n-2]交换，总共通过n-1次，得到一个按排序码从小到大排列的有序序列。

 

 

 

public class SelectSort {

    public static void main(String[] args) {
        int [] arr = {101, 34, 119, 1, -1, 90, 123};
                System.out.println("排序前");
        System.out.println(Arrays.toString(arr));
                selectSort(arr);
                System.out.println("排序后");
        System.out.println(Arrays.toString(arr));
    }
    
    //选择排序
    public static void selectSort(int[] arr) {          
        
        //在推导的过程，我们发现了规律，因此，可以使用for来解决
        //选择排序时间复杂度是 O(n^2)
        for (int i = 0; i < arr.length - 1; i++) {
            int minIndex = i;
            int min = arr[i];
            for (int j = i + 1; j < arr.length; j++) {
                if (min > arr[j]) { // 说明假定的最小值，并不是最小
                    min = arr[j]; // 重置min
                    minIndex = j; // 重置minIndex
                }
            }

            // 将最小值，放在arr[0], 即交换
            if (minIndex != i) {
                arr[minIndex] = arr[i];
                arr[i] = min;
            }

            //System.out.println("第"+(i+1)+"轮后~~");
            //System.out.println(Arrays.toString(arr));// 1, 34, 119, 101
        }
        }
}

五、插入排序

插入排序（InsertionSorting）的基本思想是：把n个待排序的元素看成为一个有序表和一个无序表，开始时有序表中只包含一个元素，无序表中包含有n-1个元素，排序过程中每次从无序表中取出第一个元素，把它的排序码依次与有序表元素的排序码进行比较，将它插入到有序表中的适当位置，使之成为新的有序表。

 

 

 

public class InsertSort {

    public static void main(String[] args) {
        int[] arr = {101, 34, 119, 1, -1, 89}; 
                insertSort(arr); //调用插入排序算法         
                System.out.println(Arrays.toString(arr));
    }
        public static void insertSort(int[] arr) {
        int insertVal = 0;
        int insertIndex = 0;
        //使用for循环来把代码简化
        for(int i = 1; i < arr.length; i++) {
            //定义待插入的数
            insertVal = arr[i];
            insertIndex = i - 1; // 即arr[1]的前面这个数的下标
    
            // 给insertVal 找到插入的位置
            // 说明
            // 1. insertIndex >= 0 保证在给insertVal 找插入位置，不越界
            // 2. insertVal < arr[insertIndex] 待插入的数，还没有找到插入位置
            // 3. 就需要将 arr[insertIndex] 后移
            while (insertIndex >= 0 && insertVal < arr[insertIndex]) {
                arr[insertIndex + 1] = arr[insertIndex];// arr[insertIndex]
                insertIndex--;
            }
            // 当退出while循环时，说明插入的位置找到, insertIndex + 1
            // 举例：理解不了，我们一会 debug
            //这里我们判断是否需要赋值
            if(insertIndex + 1 != i) {
                arr[insertIndex + 1] = insertVal;
            }
    
            //System.out.println("第"+i+"轮插入");
            //System.out.println(Arrays.toString(arr));
        }
}
}

六、希尔排序

希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止

 

 

 

 

 

 

public class ShellSort {

    public static void main(String[] args) {
        int[] arr = { 8, 9, 1, 7, 2, 3, 5, 4, 6, 0 };
                shellSort2(arr);//移位方式
                System.out.println(Arrays.toString(arr));
    }
        //对交换式的希尔排序进行优化->移位法
    public static void shellSort2(int[] arr) {
        
        // 增量gap, 并逐步的缩小增量
        for (int gap = arr.length / 2; gap > 0; gap /= 2) {
            // 从第gap个元素，逐个对其所在的组进行直接插入排序
            for (int i = gap; i < arr.length; i++) {
                int j = i;
                int temp = arr[j];
                if (arr[j] < arr[j - gap]) {
                    while (j - gap >= 0 && temp < arr[j - gap]) {
                        //移动
                        arr[j] = arr[j-gap];
                        j -= gap;
                    }
                    //当退出while后，就给temp找到插入的位置
                    arr[j] = temp;
                }

            }
        }
    }

}                          

七、快速排序

快速排序（Quicksort）是对冒泡排序的一种改进。基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列

 

 

 

public class QuickSort {

    public static void main(String[] args) {
        int[] arr = {-9,78,0,23,-567,70, -1,900, 4561};
                quickSort(arr, 0, arr.length-1);
                  System.out.println("arr=" + Arrays.toString(arr));
    }
        public static void quickSort(int[] arr,int left, int right) {
        int l = left; //左下标
        int r = right; //右下标
        //pivot 中轴值
        int pivot = arr[(left + right) / 2];
        int temp = 0; //临时变量，作为交换时使用
        //while循环的目的是让比pivot 值小放到左边
        //比pivot 值大放到右边
        while( l < r) { 
            //在pivot的左边一直找,找到大于等于pivot值,才退出
            while( arr[l] < pivot) {
                l += 1;
            }
            //在pivot的右边一直找,找到小于等于pivot值,才退出
            while(arr[r] > pivot) {
                r -= 1;
            }
            //如果l >= r说明pivot 的左右两的值，已经按照左边全部是
            //小于等于pivot值，右边全部是大于等于pivot值
            if( l >= r) {
                break;
            }
            
            //交换
            temp = arr[l];
            arr[l] = arr[r];
            arr[r] = temp;
            
            //如果交换完后，发现这个arr[l] == pivot值 相等 r--， 前移
            if(arr[l] == pivot) {
                r -= 1;
            }
            //如果交换完后，发现这个arr[r] == pivot值 相等 l++， 后移
            if(arr[r] == pivot) {
                l += 1;
            }
        }
        
        // 如果 l == r, 必须l++, r--, 否则为出现栈溢出
        if (l == r) {
            l += 1;
            r -= 1;
        }
        //向左递归
        if(left < r) {
            quickSort(arr, left, r);
        }
        //向右递归
        if(right > l) {
            quickSort(arr, l, right);
        }
        
        
    }
}

八、归并排序

归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)。

 

 

 

 

 

 

public class MergetSort {

    public static void main(String[] args) {
        int arr[] = { 8, 4, 5, 7, 1, 3, 6, 2 }; 
                int temp[] = new int[arr.length]; //归并排序需要一个额外空间
         mergeSort(arr, 0, arr.length - 1, temp);
                System.out.println("归并排序后=" + Arrays.toString(arr));
    }
        //分+合方法
    public static void mergeSort(int[] arr, int left, int right, int[] temp) {
        if(left < right) {
            int mid = (left + right) / 2; //中间索引
            //向左递归进行分解
            mergeSort(arr, left, mid, temp);
            //向右递归进行分解
            mergeSort(arr, mid + 1, right, temp);
            //合并
            merge(arr, left, mid, right, temp);
            
        }
    }
    
    //合并的方法
    /**
     * 
     * @param arr 排序的原始数组
     * @param left 左边有序序列的初始索引
     * @param mid 中间索引
     * @param right 右边索引
     * @param temp 做中转的数组
     */
    public static void merge(int[] arr, int left, int mid, int right, int[] temp) {
        
        int i = left; // 初始化i, 左边有序序列的初始索引
        int j = mid + 1; //初始化j, 右边有序序列的初始索引
        int t = 0; // 指向temp数组的当前索引
        
        //(一)
        //先把左右两边(有序)的数据按照规则填充到temp数组
        //直到左右两边的有序序列，有一边处理完毕为止
        while (i <= mid && j <= right) {//继续
            //如果左边的有序序列的当前元素，小于等于右边有序序列的当前元素
            //即将左边的当前元素，填充到 temp数组 
            //然后 t++, i++
            if(arr[i] <= arr[j]) {
                temp[t] = arr[i];
                t += 1;
                i += 1;
            } else { //反之,将右边有序序列的当前元素，填充到temp数组
                temp[t] = arr[j];
                t += 1;
                j += 1;
            }
        }
        
        //(二)
        //把有剩余数据的一边的数据依次全部填充到temp
        while( i <= mid) { //左边的有序序列还有剩余的元素，就全部填充到temp
            temp[t] = arr[i];
            t += 1;
            i += 1;    
        }
        
        while( j <= right) { //右边的有序序列还有剩余的元素，就全部填充到temp
            temp[t] = arr[j];
            t += 1;
            j += 1;    
        }
        
        
        //(三)
        //将temp数组的元素拷贝到arr
        //注意，并不是每次都拷贝所有
        t = 0;
        int tempLeft = left; // 
        //第一次合并 tempLeft = 0 , right = 1 //  tempLeft = 2  right = 3 // tL=0 ri=3
        //最后一次 tempLeft = 0  right = 7
        while(tempLeft <= right) { 
            arr[tempLeft] = temp[t];
            t += 1;
            tempLeft += 1;
        }
        
    }

}

九、基数排序

将所有待比较数值统一为同样的数位长度，数位较短的数前面补零。然后，从最低位开始，依次进行一次排序。这样从最低位排序一直到最高位排序完成以后,数列就变成一个有序序列。

 

 

 

 

 

 

 

 

 

 

public class RadixSort {

    public static void main(String[] args) {
        int arr[] = { 53, 3, 542, 748, 14, 214};
                radixSort(arr);
                System.out.println("基数排序后 " + Arrays.toString(arr));
        
    }
         //基数排序方法
    public static void radixSort(int[] arr) {
        
        //根据前面的推导过程，我们可以得到最终的基数排序代码
        
        //1. 得到数组中最大的数的位数
        int max = arr[0]; //假设第一数就是最大数
        for(int i = 1; i < arr.length; i++) {
            if (arr[i] > max) {
                max = arr[i];
            }
        }
        //得到最大数是几位数
        int maxLength = (max + "").length();
        
        
        //定义一个二维数组，表示10个桶, 每个桶就是一个一维数组
        //说明
        //1. 二维数组包含10个一维数组
        //2. 为了防止在放入数的时候，数据溢出，则每个一维数组(桶)，大小定为arr.length
        //3. 名明确，基数排序是使用空间换时间的经典算法
        int[][] bucket = new int[10][arr.length];
        
        //为了记录每个桶中，实际存放了多少个数据,我们定义一个一维数组来记录各个桶的每次放入的数据个数
        //可以这里理解
        //比如：bucketElementCounts[0] , 记录的就是  bucket[0] 桶的放入数据个数
        int[] bucketElementCounts = new int[10];
        
        
        //这里我们使用循环将代码处理
        
        for(int i = 0 , n = 1; i < maxLength; i++, n *= 10) {
            //(针对每个元素的对应位进行排序处理)， 第一次是个位，第二次是十位，第三次是百位..
            for(int j = 0; j < arr.length; j++) {
                //取出每个元素的对应位的值
                int digitOfElement = arr[j] / n % 10;
                //放入到对应的桶中
                bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
                bucketElementCounts[digitOfElement]++;
            }
            //按照这个桶的顺序(一维数组的下标依次取出数据，放入原来数组)
            int index = 0;
            //遍历每一桶，并将桶中是数据，放入到原数组
            for(int k = 0; k < bucketElementCounts.length; k++) {
                //如果桶中，有数据，我们才放入到原数组
                if(bucketElementCounts[k] != 0) {
                    //循环该桶即第k个桶(即第k个一维数组), 放入
                    for(int l = 0; l < bucketElementCounts[k]; l++) {
                        //取出元素放入到arr
                        arr[index++] = bucket[k][l];
                    }
                }
                //第i+1轮处理后，需要将每个 bucketElementCounts[k] = 0 ！！！！
                bucketElementCounts[k] = 0;
                
            }
            //System.out.println("第"+(i+1)+"轮，对个位的排序处理 arr =" + Arrays.toString(arr));
            
        }
}
}

十、堆排序

1)堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，它也是不稳定排序。

2)堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆,注意:没有要求结点的左孩子的值和右孩子的值的大小关系。

3)每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆

4)大顶堆举例说明

 

 

 5)小顶堆举例说明

 

 

 6)一般升序采用大顶堆，降序采用小顶堆

堆排序的基本思想是：

1)将待排序序列构造成一个大顶堆

2)此时，整个序列的最大值就是堆顶的根节点。

3)将其与末尾元素进行交换，此时末尾就为最大值。

4)然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了。

 要求：给你一个数组{4,6,8,5,9},要求使用堆排序法，将数组升序排序。

步骤一构造初始堆。将给定无序序列构造成一个大顶堆（一般升序采用大顶堆，降序采用小顶堆)。

原始的数组[4,6,8,5,9]

1).假设给定无序序列结构如下

 

 

 2).此时我们从最后一个非叶子结点开始（叶结点自然不用调整，第一个非叶子结点arr.length/2-1=5/2-1=1，也就是下面的6结点），从左至右，从下至上进行调整。

 

 

 3).找到第二个非叶节点4，由于[4,9,8]中9元素最大，4和9交换。

 

 

 4)这时，交换导致了子根[4,5,6]结构混乱，继续调整，[4,5,6]中6最大，交换4和6。

 

 

 

 

此时，我们就将一个无序序列构造成了一个大顶堆。

得到第二大元素。如此反复进行交换、重建、交换。

1).将堆顶元素9和末尾元素4进行交换

 

 2).重新调整结构，使其继续满足堆定义

 

 3).再将堆顶元素8与末尾元素5进行交换，得到第二大元素8

 

 4)后续过程，继续进行调整，交换，如此反复进行，最终使得整个序列有序

 

 

public class HeapSort {

    public static void main(String[] args) {
        //要求将数组进行升序排序
        int arr[] = {4, 6, 8, 5, 9};
                heapSort(arr);
                System.out.println("排序后=" + Arrays.toString(arr));
    }
         public static void heapSort(int arr[]) {
        int temp = 0;
        System.out.println("堆排序!!");
        
//        //分步完成
//        adjustHeap(arr, 1, arr.length);
//        System.out.println("第一次" + Arrays.toString(arr)); // 4, 9, 8, 5, 6
//        
//        adjustHeap(arr, 0, arr.length);
//        System.out.println("第2次" + Arrays.toString(arr)); // 9,6,8,5,4
        
        //完成我们最终代码
        //将无序序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆
        for(int i = arr.length / 2 -1; i >=0; i--) {
            adjustHeap(arr, i, arr.length);
        }
        
        /*
         * 2).将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端;
　　            3).重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序。
         */
        for(int j = arr.length-1;j >0; j--) {
            //交换
            temp = arr[j];
            arr[j] = arr[0];
            arr[0] = temp;
            adjustHeap(arr, 0, j); 
        }
        
        //System.out.println("数组=" + Arrays.toString(arr)); 
        
    }
    
    //将一个数组(二叉树), 调整成一个大顶堆
    /**
     * 功能： 完成 将 以 i 对应的非叶子结点的树调整成大顶堆
     * 举例  int arr[] = {4, 6, 8, 5, 9}; => i = 1 => adjustHeap => 得到 {4, 9, 8, 5, 6}
     * 如果我们再次调用  adjustHeap 传入的是 i = 0 => 得到 {4, 9, 8, 5, 6} => {9,6,8,5, 4}
     * @param arr 待调整的数组
     * @param i 表示非叶子结点在数组中索引
     * @param lenght 表示对多少个元素继续调整， length 是在逐渐的减少
     */
    public  static void adjustHeap(int arr[], int i, int lenght) {
        
        int temp = arr[i];//先取出当前元素的值，保存在临时变量
        //开始调整
        //说明
        //1. k = i * 2 + 1 k 是 i结点的左子结点
        for(int k = i * 2 + 1; k < lenght; k = k * 2 + 1) {
            if(k+1 < lenght && arr[k] < arr[k+1]) { //说明左子结点的值小于右子结点的值
                k++; // k 指向右子结点
            }
            if(arr[k] > temp) { //如果子结点大于父结点
                arr[i] = arr[k]; //把较大的值赋给当前结点
                i = k; //!!! i 指向 k,继续循环比较
            } else {
                break;//!
            }
        }
        //当for 循环结束后，我们已经将以i 为父结点的树的最大值，放在了 最顶(局部)
        arr[i] = temp;//将temp值放到调整后的位置
    }
    
}

 

 

 

 

 

 

 

 注：尚硅谷学习笔记

 

以上是关于数据结构-八种排序算法的主要内容，如果未能解决你的问题，请参考以下文章

java----八种排序算法

Java常用的八种排序算法与代码实现

八种常见排序算法细讲

一遍记住Java常用的八种排序算法与代码实现

一遍记住Java常用的八种排序算法与代码实现

一遍记住Java常用的八种排序算法与代码实现