BloomFilter简介

Posted 2020-12-19 reecelin

引言

之前在公司的时候接到了一个小需求，给新用户发送优惠券，优惠券功能已经借助于公司兄弟部门开发完成，我们这边只需要直接接入就行。因此，我的任务也很简单，只需要判断登录用户是否是新用户即可。

一开始拿到需求的时候，没觉得有啥，只觉得反正有数据库么，直接查一下返回true或者false不就行了。但却被我老大直接否了，说有两亿的用户，同一时间要是多人登录，数据库不要了？好吧，那就重新思考了一下。因为我们这边有很多歌曲和听书缓存，打算借鉴一下，先去缓存中查，没有就再查库后刷缓存。又被否了。。。原因是还得查库，要是第一次上线的话，内存中并没有缓存，要是大量用户同时打开，数据库还得崩；第二个就是，两亿的数据量，放在Redis这种内存数据库中，占据很大一部分空间，浪费资源。最后没办法，只好厚着脸皮去请教了组里的大神前辈，大神前辈只说让我去看看Redis的布隆过滤器。这玩意是我第一次听说，没办法，需求都排好日期了，得赶紧干完活啊。

BloomFilter 简介

日常开发中，我们常常需要面对这样一个场景，判断一个元素是否存在集合当中，如我的这个需求，判断用户是否为新用户。一般数据量比较少的时候，很好处理，Java和Redis都提供了Set这个数据结构，我们可以直接调用方法来进行判断即可。但是当数据量比较大时，无论是Java亦或者是Redis中的Set都会占据相当一部分内存，影响整体性能。因此，BloomFilter应运而生。BloomFilter可以理解为一个不怎么精确的Set结构，因为可能存在误判。为什么会存在误判呢？下面我们简要介绍一下BloomFilter。

BloomFilter原理

BloomFilter是一种概率型数据结构，它由一个长度为m的二进制向量（其实就是位数组）和k个哈希函数组成，其特点是插入和查询的效率非常高，但缺点是存在一定的误判率。

位数组初始化时各位上都是0，如下所示：

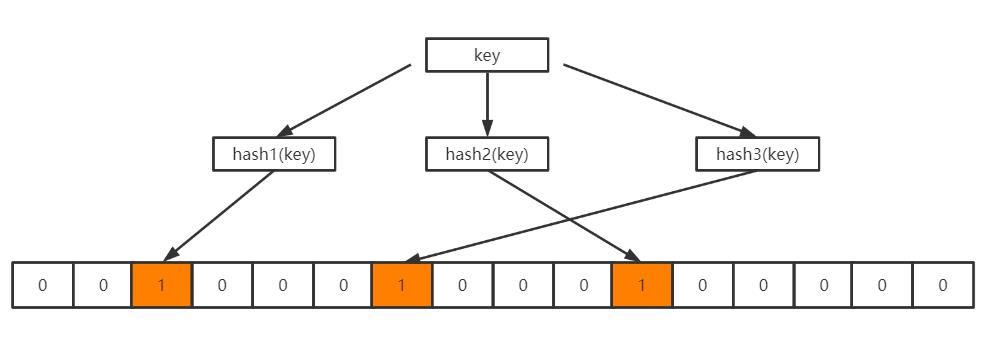
当向BloomFilter中存入一个key时，经过k个哈希函数的计算之后得到k个不同的哈希值，这些哈希值再模以位数组的长度m，得到k个数组中的位置，再将这些位置上的0修改为1，如下所示：

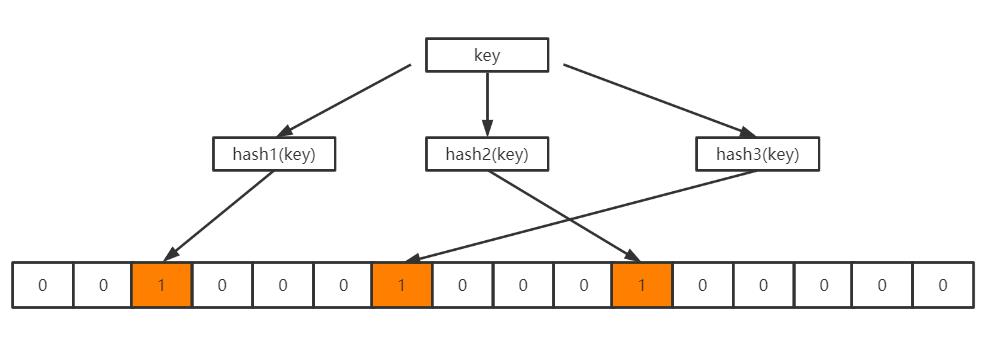
当想要查询这个key是否存在时，也很简单，通过哈希函数和位数组的长度获得key映射在位数组上的不同位置，若是有一个位置上仍是0，那么这个key就一定不存在于这个bloomFilter上。若是不同位置上都是1，则这个key有可能存在于这个BloomFilter中。为什么说是有可能呢？考虑一下下图这个场景。

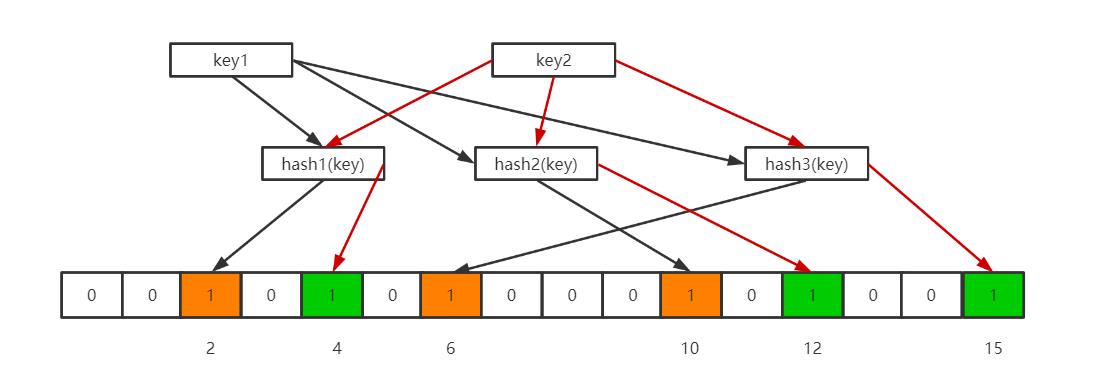
此时有key1、key2两个key在BloomFilter上，导致位数组的2,、4、6、10、12、15位置上都为1。假设现在有一个key3，经过计算之后，其在位数组上的位置分别是2、6、12。这三个位置上都是1，那么这个key3到底在不在BloomFilter里面呢？这个就不得而知了，这也是BoolFilter存在误判的原因。所以才有了那个结论：当我们搜索一个值的时候，若该值经过 k 个哈希函数运算后的任何一个索引位为 ”0“，那么该值肯定不在集合中。但如果所有哈希索引值均为 ”1“，则只能说该搜索的值可能存在集合中。一句话就是，不存在就一定不存在，存在也可能是不存在的。

误判率

既然存在误判率，那么我们怎么控制呢？还是要从BloomFilter的结构上分析。当位数组长度比较小，且哈希函数比较少时，经过n个key之后，可以预见位数组上大部分都已经是1，这个时候误判率将会非常高，因为你没办法区分位置上的1是由key自身生成的，还是设置其他key导致的。所以，误判率是由哈希函数的个数k、位数组长度m以及key个数n共同决定的，公式如下所示：

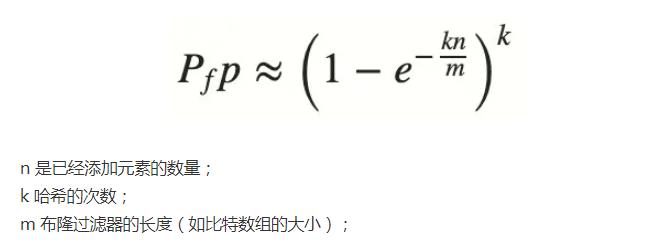
极端情况下，当BloomFilter没有空闲空间的时候，每一次查询都会返回true。这就意味着我们在初始化BloomFilter时要预估好key的个数和位数组长度m，需要使得m远远大于n。

位数组长度m可以根据预估误判率FFP和预估key的数量计算得到，如下所示：

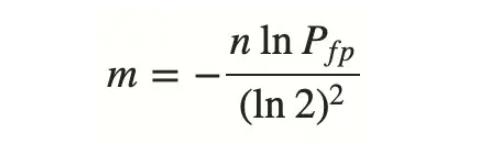
具体的数学推导，可以参考这篇文章。

当位数组长度m确定之后，哈希函数个数k可以依靠下面公式大概估计出来：

k=0.7*(m/n)
k，最佳哈希次数，即哈希函数的个数；
m，位数组长度；
n，期望添加的key数量

上面的公式计算起来可能比较麻烦，网上有人提供了一个网址，可以直接刷入相关参数来获得具体的值，有兴趣的话可以自己看一下，布隆计算器。

假如在使用BloomFilter时，位数组长度设置有误，导致最后添加的key数量n大于位数组长度m时，误判率会如何变化。这时候另一个公式派上用场：

f=(1-0.5^t)^k 
t,实际key数量与预估key数量之比
k，哈希函数个数

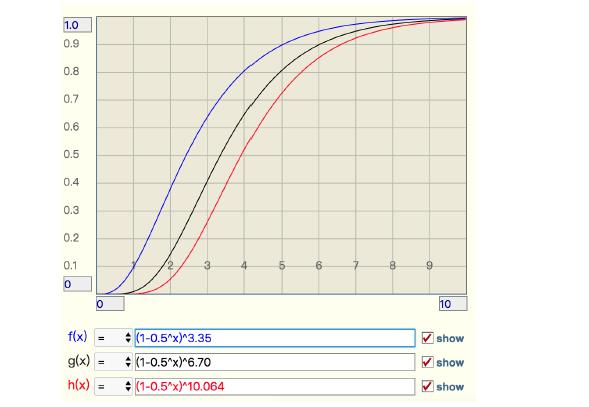
上图出自《Redis深度历险：核心原理和应用实践》中，关于t增大时，误判率的变化。可以发现t增大时，误判率将会增大。

BloomFilter 实践

整合代码放到了这里，感兴趣的可以看一下，BloomFilter实现新用户判断。

参考

[布隆过滤器(Bloom Filter)的原理和实现]

5 分钟搞懂布隆过滤器，亿级数据过滤算法你值得拥有！

[布隆过滤器 (Bloom Filter) 详解]

在redis中使用BloomFilter布隆过滤器

《Redis深度历险：核心原理和应用实践》