最新情报：所有的递归都可以改写成非递归？

Posted 2020-12-19 tong-yuan

前言

本文收录于专辑：http://dwz.win/HjK，点击解锁更多数据结构与算法的知识。

你好，我是彤哥，一个每天爬二十六层楼还不忘读源码的硬核男人。

上一节，我们使用位图介绍了12306抢票算法的实现，没有收到推送的同学可以点击上方专辑查看，或者在公主号历史消息中查看。

在上一节的最后，彤哥收到最新情报，说是所有的递归都可以改写成非递归，是不是真的呢？如何实现呢？有没有套路呢？

让我们带着这些问题进入今天的学习吧。

何为递归？

所谓递归，是指程序在运行的过程中调用自身的行为。

这种行为也不能无限制地进行下去，得有个出口，叫做边界条件，所以，递归可以分成三个段：前进段、达到边界条件，返回段，在这三个段我们都可以做一些事，比如前进段对问题规模进行缩小，返回段对结果进行整理。

这么说可能比较抽象，让我们看一个简单的案例：

如何用递归实现1到100的相加？

1到100相加使用循环大家都会解，代码如下：

public class Sum {
    public static void main(String[] args) {
        System.out.println(sumCircle(1, 100));
    }

    private static int sumCircle(int min, int max) {
        int sum = 0;
        for (int i = min; i <= max; i++) {
            sum += i;
        }
        return sum;
    }
}

那么，如何使用递归实现呢？

如何快速实现递归？

首先，我们要找到这道题的边界条件，1到100相加，边界条件可以是1，也可以是100，如果从1开始，那么边界条件就是100，反之亦然。

找到了边界条件之后，就是将问题规模缩小，对于这道题，计算1到100相加，那么，能不能先计算1到99相加再把100加上呢？肯定是可以的，这样问题的规模就缩小了，直到，问题规模缩小为1到1相加为止。

OK，让我们看代码实现：

private static int sumRecursive(int min, int max) {
    // 边界条件
    if (min >= max) {
        return min;
    }
    // 问题规模缩小
    int sum = sumRecursive(min, max - 1);
    // 加上当前值
    sum += max;
    // 返回
    return sum;
}

是不是很简单？还可以更简单：

private static int sumRecursive2(int min, int max) {
    return min >= max ? min : sumRecursive2(min, max - 1) + max;
}

686?

所以，使用递归最重要的就是找到边界条件，然后让问题的规模朝着边界条件的方向一直缩小，直到达到边界条件，最后依次返回即可，这也是快速实现递归的套路。

这么看来，使用递归似乎很简单，但是，它有没有什么缺点呢？

要了解缺点就得从递归的本质入手。

递归的本质是什么？

我们知道，JVM启动的时候有个参数叫做-Xss，它不是表示XSS攻击哈，它是指每个线程可以使用的线程栈的大小。

那么，什么又是线程栈呢？

栈大家都理解了，我们在前面的章节也学习过了，使用栈，可以实现计算器的功能，非常方便。

线程栈，顾名思义，就是指线程运行过程中使用的栈。

那么，线程在运行的过程中为什么要使用栈呢？

这就不得不说方法调用的本质了。

举个简单的例子：

private static int a(int num) {
    int a = 1;
    return a + b(num);
}

private static int b(int num) {
    int b = 2;
    return c(num) + b;
}

private static int c(int num) {
    int c = 3;
    return c + num;
}

在这段代码中，方法a() 调用 方法b()，方法b() 调用 方法c()，在实际运行的过程中，是这样处理的：调用方法a()时，发现需要调用方法b()才能返回，那就把方法a()及其状态保存到栈中，然后调用方法b()，同样地，调用方法b()时，发现需要先调用方法c()才能返回，那就把方法b()及其状态入栈，然后调用方法c()，调用方法c()时，不需要额外调用别的方法了，计算完毕返回，返回之后，从栈顶取出方法b()及当时的状态，继续运行方法b()，方法b()运行完毕，返回，再从栈中取出方法a()及当时的状态，计算完毕，方法a()返回，程序等待结束。

还是上图吧：

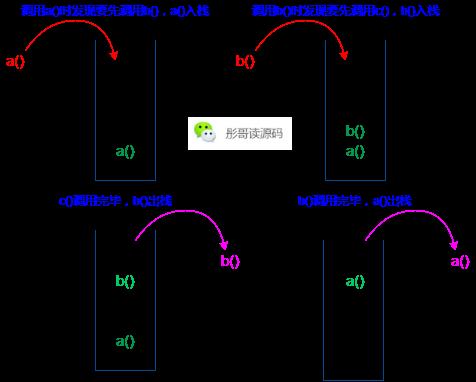
所以，方法调用的本质，就是栈的使用。

同理，递归的调用就是方法的调用，所以，递归的调用，也是栈的使用，不过，这个栈会变得非常大，比如，对于1到100相加，就有99次入栈出栈的操作。

因此，总结起来，递归有以下两个缺点：

1. 操作耗时，因为牵涉到大量的入栈出栈操作；
2. 有可能导致线程栈溢出，因为递归调用占用了线程栈很大的空间。

那么，我们是不是就不要使用递归了呢？

当然不是，之所以使用递归，就是因为它使用起来非常简单，能够快速地解决我们的问题，合理控制递归调用链的长度，就是一个好递归。

既然，递归调用的本质，就是栈的使用，那么，我们能不能自己模拟一个栈，将递归调用改成非递归呢？

当然可以。

修改递归为非递归的套路

还是使用上面的例子，现在我们需要把递归修改成非递归，且不是使用for循环的那种形式，要怎么实现呢？

首先，我们要自己模拟一个栈；

然后，找到边界条件；

最后，朝着边界条件的方向缩小问题规模；

OK，上代码：

private static int sumNonRecursive(int min, int max) {
        int sum = 0;
        // 声明一个栈
        Stack<Integer> stack = new Stack<Integer>();
        stack.push(max);
        while (!stack.isEmpty()) {
            if (max > min) {
                // 要计算max，先计算max-1
                stack.push(--max);
            } else {
                // 问题规模缩小到一定程度，计算返回
                sum += stack.pop();
            }
        }
        return sum;
    }

好了，是不是很简单，其实跟递归的套路是一样的，只不过改成自己模拟栈来实现。

这个例子可能不是那么明显，我们再举个二叉树遍历的例子来看一下。

public class BinaryTree {

    Node root;

    // 插入元素
    void put(int value) {
        if (root == null) {
            root = new Node(value);
        } else {
            Node parent = root;
            while (true) {
                if (value <= parent.value) {
                    if (parent.left == null) {
                        parent.left = new Node(value);
                        return;
                    } else {
                        parent = parent.left;
                    }
                } else {
                    if (parent.right == null) {
                        parent.right = new Node(value);
                        return;
                    } else {
                        parent = parent.right;
                    }
                }

            }
        }
    }

    // 先序遍历
    void preTraversal(Node x) {
        if (x == null) return;
        System.out.print(x.value + ",");
        preTraversal(x.left);
        preTraversal(x.right);
    }

    static class Node {
        int value;
        Node left;
        Node right;

        public Node(int value) {
            this.value = value;
        }
    }

    public static void main(String[] args) {
        BinaryTree binaryTree = new BinaryTree();
        binaryTree.put(3);
        binaryTree.put(1);
        binaryTree.put(2);
        binaryTree.put(7);
        binaryTree.put(8);
        binaryTree.put(5);
        binaryTree.put(4);
        binaryTree.put(6);
        binaryTree.put(9);
        binaryTree.put(0);

        binaryTree.preTraversal(binaryTree.root);
    }
}

我这里随手写了一颗二叉树，并实现了其先序遍历，这个测试用例中的二叉树长这个样子：

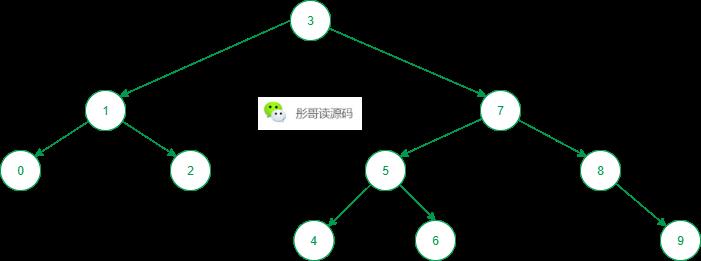
所以，这个二叉树的先序遍历结果为3,1,0,2,7,5,4,6,8,9,。

可以看到，使用递归先序遍历二叉树非常简单，而且代码清晰易懂，那么，它如何修改为非递归实现呢？

首先，我们要自己模拟一个栈；

然后，找到边界条件，为节点等于空时；

最后，缩小问题规模，这里是先把右子树压栈，再把左子树压栈，因为先左后右；

好了，来看代码实现：

// 先序遍历非递归形式
void nonRecursivePreTraversal(Node x) {
    // 自己模拟一个栈
    Stack<Node> stack = new Stack<Node>();
    stack.push(x);
    while (!stack.isEmpty()) {
        Node tmp = stack.pop();
        // 隐含的边界条件
        if (tmp != null) {
            System.out.print(tmp.value + ",");
            // 缩小问题规模
            stack.push(tmp.right);
            stack.push(tmp.left);
        }
    }
}

掌握了这个套路是不是把递归改写为非递归非常简单，不过，改写之后的代码显然没有递归那么清晰。

好了，递归改写为非递归的套路我们就讲到这里，不知道你Get到了没有呢？你也可以找个递归自己来改写试试看。

后记

本节，我们从递归的概念入手，学习了如何快速实现递归，以及递归的本质，最后，学习了递归改写为非递归的套路。

本质上，这也是栈这种数据结构的常规用法。

既然讲到了栈，不讲队列是不是有点过分？

所以，下一节，遍历各种源码的彤哥将介绍如何实现高性能的队列，想了解其中的套路吗？还不快点来关注我！

关注公号主“彤哥读源码”，解锁更多源码、基础、架构知识。