字符串匹配算法

Posted 2020-12-19 jiezao

1.1BF算法

其实就是暴力解法，直接双重循环，干就完事了。虽然算不上什么好方法，但是非常简单。对于所有的暴力算法，我们应该思考如何进行优化，比如BF算法，当我们遇到不匹配字符的时候，只能从头的下一个字符开始匹配。这样其实做了很多无用的重复工作。那么我们可以怎样优化呢？下面介绍两种。二者的思想都是避免无用功的移动。

1.2BM算法

BM算法是从匹配串的后往前匹配。遇到不匹配的字符时，将被匹配串向后移动到匹配字符或者移动到匹配串头。然后再从后往前匹配。
字符串与搜索词头部对齐，从尾部字符开始比较：

这里右移长度有一个规则一：step_bad = pos1 - pos2
step_bad表示向后移动位数；pos1表示坏字符的位置；pos2表示坏字符在搜索词中出现的最右位置（如果不存在就取值为-1）

单是这一条规则并不能保证移动后移长度最合适，我们还需要加一条好后缀规则：step_good = pos1 - pos2
step_good为后移位数；pos1表示好后缀的位置；pos2表示好后缀在搜索词中剩余部分出现的最右位置；

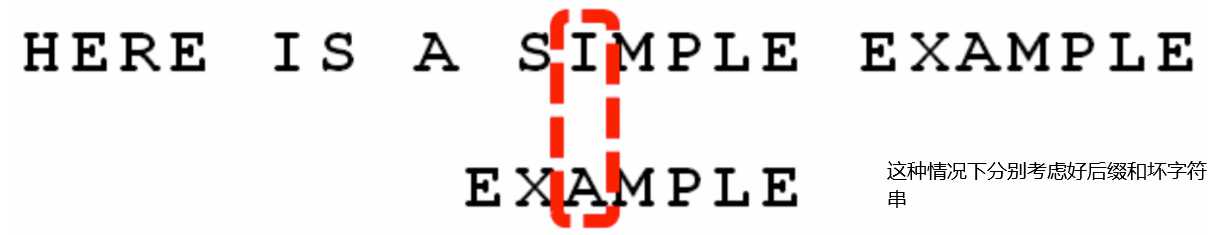
我们发现step_bad 为3 step_good为6，所以我们右移6位。

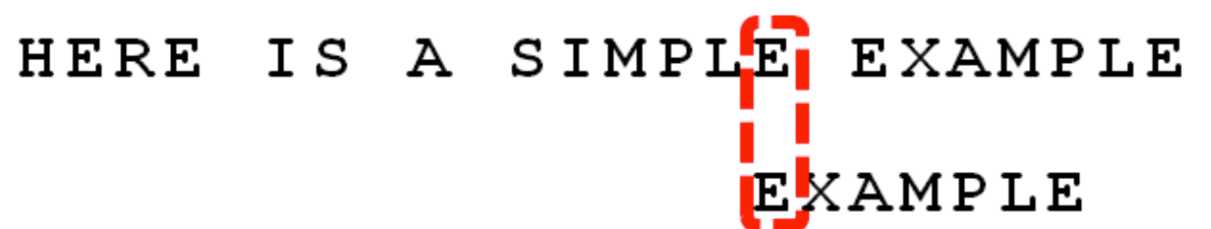
直到最后得出结果

• 代码

package matchstring;

import java.util.Arrays;

/**
 * JavaTest
 *
 * @author : xgj
 * @description : BM算法
 * @date : 2020-07-31 22:40
 **/
public class BM {

    public static int pattern(String target , String pattern) {
        int tLen = target.length();
        int pLen = pattern.length();

        if (pLen > tLen) {
            return -1;
        }

        int[] badTable = buildBadTable(pattern);
        int[] goodTable = buildGoodTable(pattern);

        for (int i = pLen - 1, j; i < tLen; ) {
            System.out.println("跳跃位置：" + i);
            for (j = pLen - 1; target.charAt(i) == pattern.charAt(j); i--, j--) {
                if (j == 0) {
                    System.out.println("匹配成功，位置：" + i);

                    return i;
                }
            }
            i += Math.max(goodTable[pLen - j - 1], badTable[target.charAt(i)]);
        }
        return -1;
    }

    /**
     * 字符信息表
     */
    public static int[] buildBadTable(String pattern) {
        final int tableSize = 256;
        int[] badTable = new int[tableSize];
        int pLen = pattern.length();

        Arrays.fill(badTable, pLen);
        for (int i = 0; i < pLen - 1; i++) {
            int k = pattern.charAt(i);
            badTable[k] = pLen - 1 - i;
        }
        return badTable;
    }

    /**
     * 匹配偏移表。
     *
     * @param pattern 模式串
     * @return
     */
    public static int[] buildGoodTable(String pattern) {
        int pLen = pattern.length();
        int[] goodTable = new int[pLen];
        int lastPrefixPosition = pLen;

        for (int i = pLen - 1; i >= 0; --i) {
            if (isPrefix(pattern, i + 1)) {
                lastPrefixPosition = i + 1;
            }
            goodTable[pLen - 1 - i] = lastPrefixPosition - i + pLen - 1;
        }

        for (int i = 0; i < pLen - 1; ++i) {
            int glen = suffixLength(pattern, i);
            goodTable[glen] = pLen - 1 - i + glen;
        }
        return goodTable;
    }

    /**
     * 前缀匹配
     */
    private static boolean isPrefix(String pattern, int p) {
        int patternLength = pattern.length();
        for (int i = p, j = 0; i < patternLength; ++i, ++j) {
            if (pattern.charAt(i) != pattern.charAt(j)) {
                return false;
            }
        }
        return true;
    }

    /**
     * 后缀匹配
     */
    private static int suffixLength(String pattern, int p) {
        int pLen = pattern.length();
        int len = 0;
        for (int i = p, j = pLen - 1; i >= 0 && pattern.charAt(i) == pattern.charAt(j); i--, j--) {
            len += 1;
        }
        return len;
    }

}

1.3KMP算法

BM是以被匹配串尾部为基准的话，KMP算法就是以被匹配串头部为基准。相对于而言KMP算法更加接近人的思考方式。
对于暴力算法，在出现不匹配的时候，我们是一位一位的往右移的。但是实际上要是人手工来做的话，会容易发现有时候可以一次移动多位。例如“SSSSSSSSSSSSSA”中查找“SSSSB”。要是人眼比较对于前面的s移动时，会一次性移动到倒数第二位，而不是一位一位的移动。那么在计算机中我们怎么实现聪明的移动呢？“利用已经部分匹配这个有效信息，保持i指针不回溯，通过修改j指针，让模式串尽量地移动到有效的位置”

• 代码

package matchstring;

/**
 * JavaTest
 *
 * @author : xgj
 * @description : KMP算法
 * @date : 2020-07-31 22:24
 **/
public class KMP {
    /**
     *功能描述 : 匹配字符串
     *
     * @author xgj
     * @date 2020/7/31
     * @param s
     * @param t
     * @return boolean
     */
    public static boolean matchString(String s, String t) {
        int[] next = getNext(t);
        char[] sArr = s.toCharArray();
        char[] tArr = t.toCharArray();
        int i = 0, j = 0;
        while (i < sArr.length && j < tArr.length) {
            if (j == -1 || sArr[i] == tArr[j]) {
                i++;
                j++;
            } else {
                j = next[j];
            }
        }
        return j == tArr.length;

    }

    /**
     *功能描述 : 返回next数组
     *
     * @author xgj
     * @date 2020/7/31
     * @param ps
     * @return int[]
     */
    public static int[] getNext(String ps) {
        char[] p = ps.toCharArray();
        int[] indexArray = new int[p.length];
        indexArray[0] = -1;
        int j = 0;
        int k = -1;
        while (j < p.length - 1) {
            if (k == -1 || p[j] == p[k]) {
                if (p[++j] == p[++k]) {
                    indexArray[j] = indexArray[k];
                } else {
                    indexArray[j] = k;
                }
            } else {
                k = indexArray[k];
            }
        }
        return indexArray;
    }
}