0-1背包（动态规划）

Posted 2020-12-19 guoyu1

1、题目描述：

 　　有 n 件物品和一个最大承重为 W 的背包，每件物品的重量是 ??i、价值是 ??i

• 在保证总重量不超过 W 的前提下，选择某些物品装入背包，背包的最大总价值是多少？

注意：每个物品只有 1 件，也就是每个物品只能选择 0 件或者 1件。

• 假设 values 是价值数组，weights 是重量数组
• 编号为 k 的物品，价值是 values[k]，重量是 weights[k]，k ∈ [0, n)

2、思路：

（1）定义状态：假设 dp(i, j) 是 最大承重为 j、有前 i 件物品可选 时的最大总价值，i ∈ [1, n]，j ∈ [1, W]

（2）状态转移方程：

?如果 j < weights[i – 1]，那么 dp(i, j) = dp(i – 1, j)

?如果 j ≥ weights[i – 1]，那么 dp(i, j) = max { dp(i – 1, j), dp(i – 1, j – weights[i – 1]) + values[i – 1] } 

（3）初始值：

?dp(i, 0)、dp(0, j) 初始值均为 0

（4）最终结果：

dp[values.length][capacity]

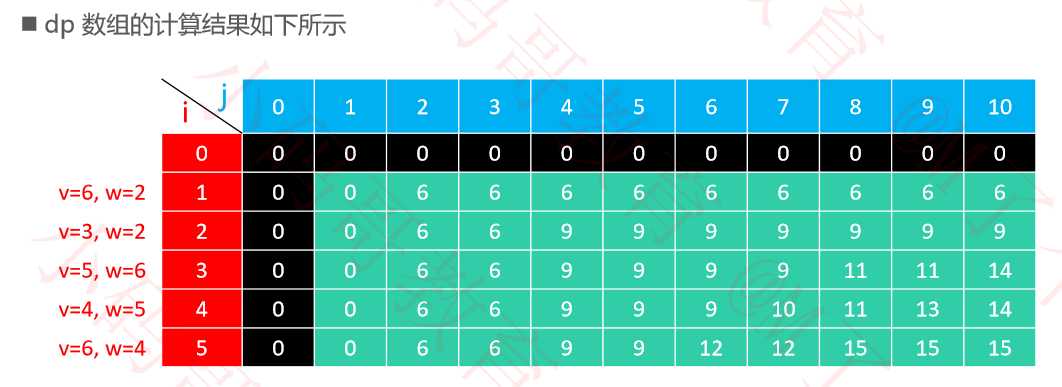
3、代码：