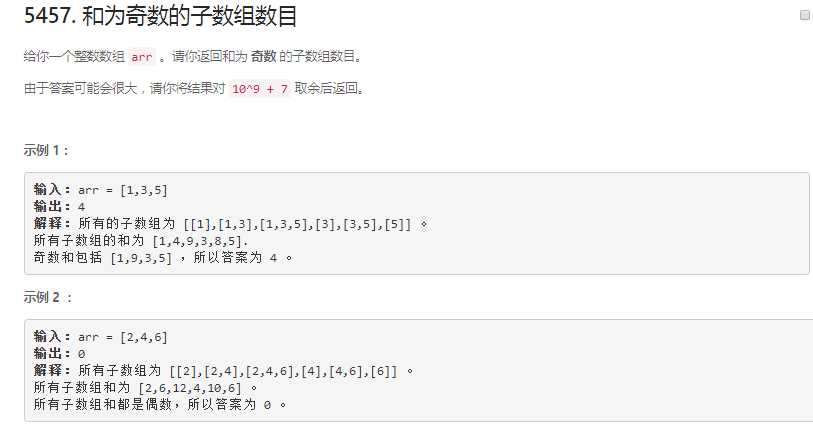
5457. 和为奇数的子数组数目

Posted 2020-12-19 sbb-first-blog

 

 

 

 

 1 int numOfSubarrays(int* arr, int arrSize){
 2     int i,j,k,n=0;
 3 //    long a[arrSize+1];
 4     int index=0;
 5      while(n <= arrSize){//当子数组长度等于原数组长度说明所有子数组已经遍历完
 6             for(int i = 0;i <= arrSize-n;i++)
 7             {//遍历长度等于len的子数组
 8                 int subSum = 0;//记录当前数组和
 9                 for(int j = i;j <= i + n -1;j++ )
10                 {//计算子数组的和
11                     subSum += arr[j];
12                 }
13                 if(subSum%2!=0)
14                 {//重新对sum赋值
15                     index++;
16                 }
17             }
18          n++;
19      }
20  return index%1000000007;
21 }

 此种情况会出现超时的情况，并且计算的是所有子数组的和与题目要求的不一样。题目中例如[1,3,5]只是计算[1],[1,3],[1,3,5],[3],[3,5],[5]这种连续的。并不计算[1，5]这种不连续的子数组。

 1 int numOfSubarrays(int* arr, int arrSize){
 2     long long sum=0,even=1,odd=0;
 3 //even为偶数的计量，因为[]也是一种情况偶数情况，故even为1，odd为奇数的计量。
 4     int ans=0;
 5     for(int i=0;i<arrSize;i++)
 6     {
 7         sum+=arr[i];
 8         if(sum%2==1)
 9         {
10             ans+=even;
11             odd++;
12         }
13         else{
14             ans+=odd;
15             even++;
16         }
17         ans%=1000000007;
18     }
19 return ans;
20 }

参考文章：

解题思路：

题目要求数组里, 连续元素构成的子数组的和 为 奇数 的 cnt. 其实连续子数组的元素 也就是子串.

需要一定的熟练度, 想到是可以通过前缀和来做的.

以及奇 偶 间的关系:
奇 - 偶 = 奇;
偶 - 奇 = 奇;

=>

[0, i]上的(前缀)和 -− [0, k]某个(前缀)和/ []空区间 = 奇数; 其中,k∈[0,i−1].
这个情况就是我们想要的.
在这里举个例子, 然后举2个情况, 解释对应例子下的情况:

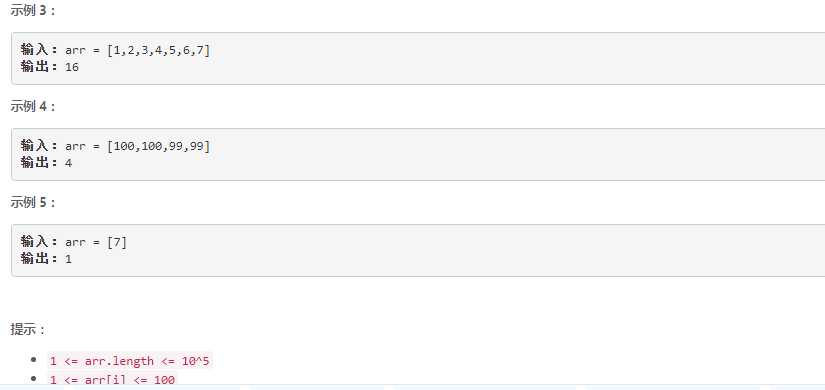
输入：arr=[1,3,5]
输出：4
解释：所有的子数组为[[1],[1,3],[1,3,5],[3],[3,5],[5]]。
所有子数组的和为[1,4,9,3,8,5].
奇数和包括[1,9,3,5]，所以答案为4。
这里的:
子数组和=1时,[1]=[1]−[],                                             i=0和[]空间, [0,0]上的和=[0,0]上得前缀和−[ ]
子数组和=4时,[1,3]=[1,3]−[],...,...
子数组和=9时,[1,3,5]=[1,3,5]−[],...,..
子数组和=3时,[3]=[1,3]−[1],                                         i=1和k=0, [1,1]上的和=[0,1]上的前缀和−[0,0]上的前缀和
子数组和=8时,[3,5]=[1,3,5]−[1],...,..
子数组和=5时,[5]=[1,3,5]−[1,3],...,..

我们需要判断[0, i]上的(前缀)和 是不是 为奇/ 偶数, 从而 得到这里的减数 是 偶/ 奇数.

[0, i]上的子数组和为奇数的cnt=([0, i]上的(前缀)和 为奇数 - [0, k]某个(前缀)和 为 偶数) 的情况个数+([0, i]上的(前缀)和 为偶数 - [0, k]某个(前缀)和 为 奇数) 的情况个数

作者：bovenpeng
链接：https://leetcode-cn.com/problems/number-of-sub-arrays-with-odd-sum/solution/qian-zhui-he-shu-xue-by-bovenpeng/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

以下是本人关于上面解释。对例子的分析。

 

 第三种方法：

直接用数学方法解。这是参考大佬的解释，我就直接上大佬的思路了

统计一下前缀和中有几个奇数几个偶数，答案其实就是 奇数的个数×偶数的个数+奇数的个数

从前缀和里随意选出两个数做差，差值就是子数组的和，当选出的两个数是一个奇数一个偶数时，
子数组的和是奇数，所以这样的选法一共有 奇数的个数×偶数的个数 这么多种

作者：brillant_o-
链接：https://leetcode-cn.com/problems/number-of-sub-arrays-with-odd-sum/solution/python-qian-zhui-he-qi-ou-by-brillant_o-/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

 1 int numOfSubarrays(int* arr, int arrSize){
 2     long long odd=0,even=0,sum=0;
 3     for(int i=0;i<arrSize;i++)
 4     {
 5         sum+=arr[i];
 6         if(sum%2!=0)
 7         {
 8             odd++;
 9         }
10         else{
11             even++;
12         }
13     }
14     return (odd*even+odd)%1000000007;
15 
16 }