SPOS2019-arxiv-Single Path One-Shot Neural Architecture Search with Uniform Sampling
Posted chenbong
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了SPOS2019-arxiv-Single Path One-Shot Neural Architecture Search with Uniform Sampling相关的知识,希望对你有一定的参考价值。
SPOS
2019-arxiv-Single Path One-Shot Neural Architecture Search with Uniform Sampling
- Institute:MEGVII、THU、HKUST
- Author:Zichao Guo、Xiangyu Zhang、Jian Sun
- GitHub:
- https://github.com/CanyonWind/Single-Path-One-Shot-NAS-MXNet【120+】
- https://github.com/megvii-model/SinglePathOneShot【120+】
- https://github.com/megvii-model/SinglePathOneShot【120+】
- Citation:116
Introduction
构建一个简化的超网,在训练阶段,每次训练单条路径,减少权重耦合;在搜索阶段使用EA算法。
-
训练(超网)阶段:随机抽single path进行训练
-
搜索(子网)阶段:使用EA算法搜索满足特定限制(FLOPs,latency)的子网
训练,搜索两阶段思路清晰,简单有效,ablation study实验丰富。
Motivation
基于weight-sharing的NAS方法存在2个问题:
-
子网权重耦合的问题:子网的权重之间存在高度耦合,直接继承超网的权重,而且权重对子网仍然有效,没有理论依据(超网中不同的路径被训练的程度不同,有的路径被训练得多,有的被训练得少)
-
结构参数和网络权重耦合的问题:搜索空间松弛(离散化=>连续化,如DARTS系列)的基于梯度的方法中,结构参数(arch parameter)和网络权重(weight)联合优化,容易陷入“强化初始的选择“的局部最优当中去;(如第一次随机选择/抽样了某个子网,这个子网上路径上的权重会被训练,后续选择的过程中,这个子网路径上的性能表现更好,更容易被抽到,就陷入一直强化第一次选择的子网的过程,有的路径被一直训练,而有的路径没有得到充分训练。因此初始的随机选择对结果影响非常大,收敛后可能只是局部最优)
一些one-shot工作* 不使用可微分方法联合优化结构参数(arch parameter)和网络权重(weight),解决了第二个问题,将“超网训练”和“结构搜索”两个过程分离开来。
但第一个问题仍然存在,即子网络之间参数耦合的问题。【ProxylessNAS】 等使用Path Dropout的超参数来减少路径之间的耦合,但实验结果对超参非常敏感,超参的选择困难且超网比较难训练。
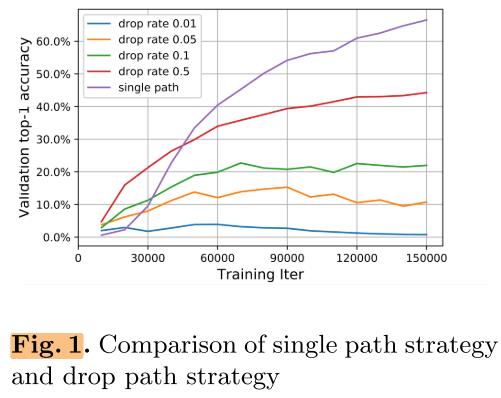
*这里的one-shot指的是狭义上的one-shot,即不使用可微分方法的超网抽样子网的方法,如【Understanding One-Shot NAS】和SMASH,广义上DARTS系列使用可微分的方法也属于one-shot
Contribution
为了解决以上2个问题,
- 提出了一种简单的训练方式(single path),每个路径都会被等概率地充分训练,后续抽样的时候不同路径的训练程度都相同,来解决子网络权重耦合问题;
- 提出了有效的搜索方式(EA),将超网训练和子网搜索分离为2个单独的步骤,解耦网络权重与网络结构的关系,同时可以容易实现各种约束(FLOPs,latency),而且是hard约束(使用EA多次搜索,直到搜索到满足约束条件的子网),而不是soft约束(比如在loss上加latency损失项就属于soft约束,soft约束只能将网络大致限制在某个值,可以理解为多个损失项之间的权衡,如果一个网络acc loss 非常小,可以牺牲一点latency约束,所以不能实现精确的约束)。
Method
训练超网阶段
(W_{mathcal{A}}=underset{W}{operatorname{argmin}} mathcal{L}_{operatorname{train}}(mathcal{N}(mathcal{A}, W)) qquad(6))
A代表超网的结构参数,W代表超网中所有的weights
(W_{mathcal{A}}=underset{W}{operatorname{argmin}} mathbb{E}_{a sim Gamma(mathcal{A})}left[mathcal{L}_{operatorname{train}}(mathcal{N}(a, W(a))) ight] qquad (8))
(mathbb{E}_{a sim Gamma(mathcal{A})}) 表示a是在A中均匀采样
搜索子网阶段
(a^{*}=underset{a in mathcal{A}}{operatorname{argmax}} mathrm{ACC}_{ ext {val }}left(mathcal{N}left(a, W_{mathcal{A}}(a) ight) ight) qquad (7))
a表示子网的结构参数,a*表示最佳子网的结构参数
搜索最佳的子网(的结构参数)
搜索空间:
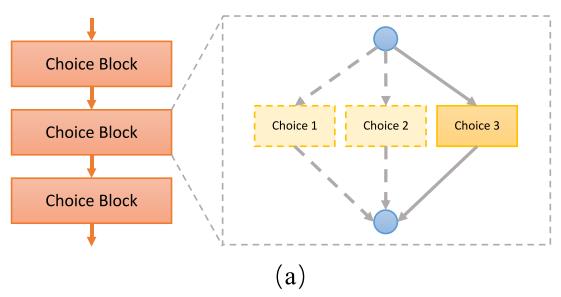

搜索空间中的输入通道数,和输出通道数可以看做“最大通道数”,实际搜索到的子网的通道数是<=“最大通道数”的。
搜索使用EA算法:

EA搜索与随机搜索的比较:
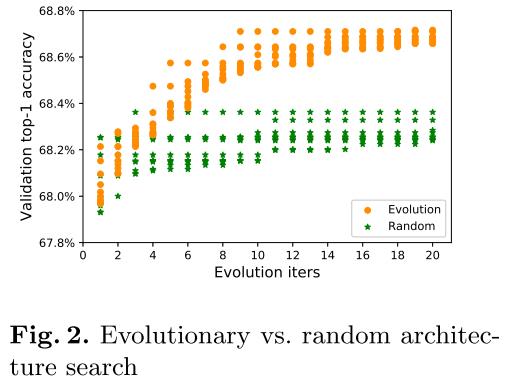
还可以搜索通道数和混合精度。
搜索通道数:
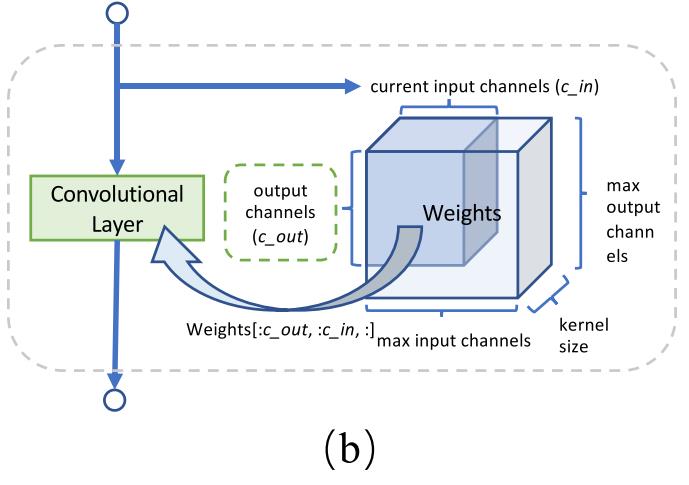
细节:如何选择通道数,每个layer预先设置有max c_in ,max c_out,kernel size*,因此这个layer的最大参数量为 kernel_size × max_c_in × max_c_out,每次抽样的c_in由上个layer的c_out决定,c_in在<=max_c_in的范围内随机抽样,可以看出,不同的iter中抽到的该层的通道数都不相同,而这些参数又是共享的,多次抽样下,(作者说)会很快收敛。
*如果 kernel 为3×3,那么这里的kernel size=9
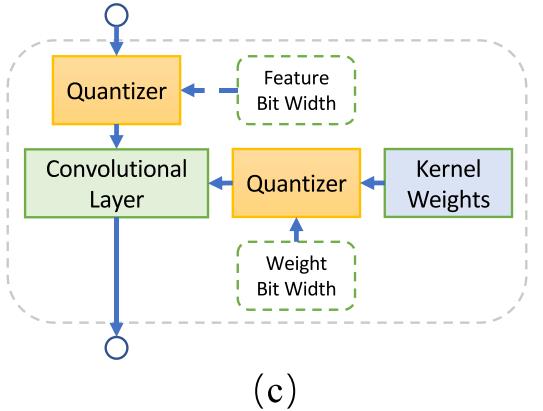
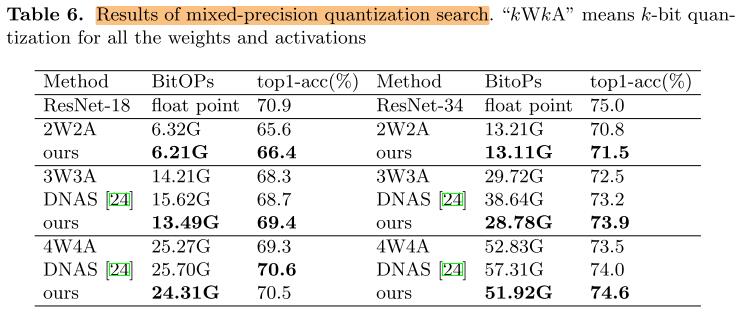
搜索混合精度
这部分不是很熟,先把结果放上来,后续再学习。
Experiments
batch size 1024,8*1080ti
supernet:120 epochs
best arch:240 epochs
整个网络共有20个choice blocks

总体结构如下表:
每个choice block有4种候选(分别是choice_3, choice_5, choice_7, choice_x),共有20个choice blocks,因此搜索空间一共是(4^{20})

由于之前大多数NAS的工作与手工设计网络的大小都在[300, 330],因此我们将FLOPs限制在<=330M
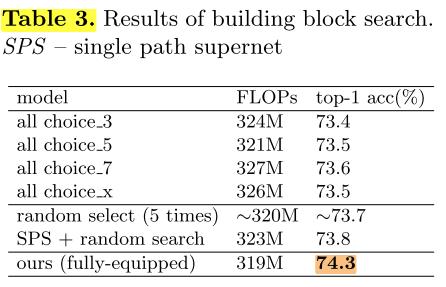
说明:
1)第一部分:不同的choice_x block的FLOPs是不同的,因此我们调整(搜索?)不同的channels来满足FLOPs约束;全部使用单一种类的blocks(我的理解是,比如全部使用choice_3的block构建超网,训练超网,在超网中随机搜索出满足FLOPs约束的子网络,重新训练)
2)第二部分:在整个搜索空间(由4种block构建的spuernet)中随机搜索 和 在single path supernet中随机搜索;使用single path训练的spuer net搜索空间只比第一种略高。(我的理解是,第一种:由4种blocks构建的supernet,直接训练,然后随机搜索;第二种:由4种blocks构建的spuernet,使用single path训练,然后随机搜索)
3)第三部分:在使用single path训练过后的supernet中将随机搜索替换为EA搜索,效果比随机搜索高了0.5个点(74.3,这里的搜索在下文中被称为block search,我的理解是,这里搜索的子网每一层用的都是最大通道数)。
为了进一步提高acc,我们同时搜索 blcoks 和 channels:
这里有2种策略:
1)在best block search 的结果上,执行channels search
2)直接同时搜索 blocks 和 channels
实验表明,第一种稍微好一点
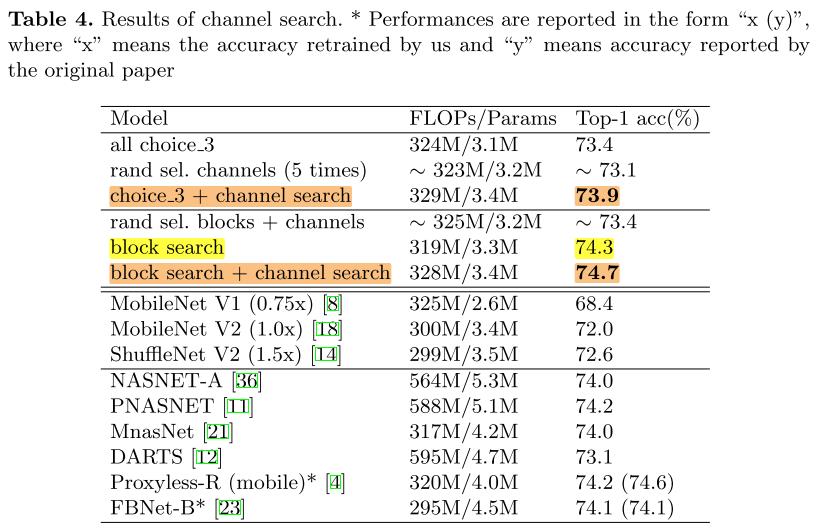
与其他SOTA的比较(使用相同的搜索空间):
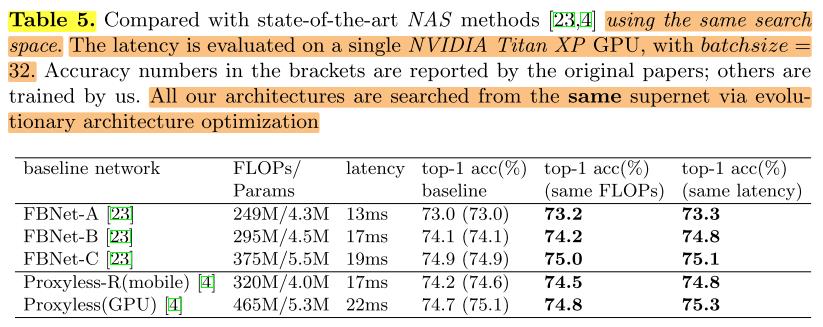
有一些工作认为性能差异只是搜索空间设计的不同,在相同的搜索空间上,有些NAS的搜索策略与随机搜索策略几乎没有区别。
因此我们在NAS-Bench-201的子集上进行搜索,使用Kendall Tau metric评估我们搜索算法的好坏。
NAS-Bench-201包含有1.5w个网络结构,并提供这些结构在cifar-10,cifar-100,ImageNet-16-120数据集上的(充分训练后的)真实性能。
NAS-Bench-201有搜索空间有5种操作:
zeroize, skip connection, 1-by-1 convolution, 3-by-3 convolution, and 3-by-3 average pooling
我们将:
删除1-by-1 conv 操作后的搜索空间叫做:Reduce-1
删除3-by-3 avg pool 操作后的搜索空间叫做:Reduce-2
两个操作都删除的搜索空间叫做:Reduce-3
在这3个搜索空间上搜索的结果:
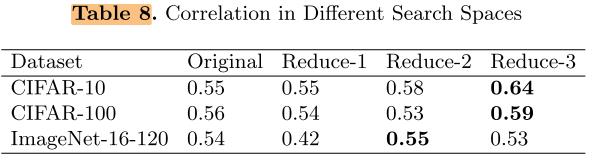
根据Kendall Tau metric的定义,τ∈[-1, 1],随机搜索τ=0,我们的结果>0,即正相关,但依然不够好,即正相关性不够
发现:越简单的搜索空间,我们的搜索算法正相关性越强
Conclusion
Summary
Reference
https://chengfeng96.com/blog/2020/07/09/NAS-学习笔记(八)-Single-Path-One-Shot-NAS/
http://www.moonjian.top/2019/09/13/NAS-Reading-5/
以上是关于SPOS2019-arxiv-Single Path One-Shot Neural Architecture Search with Uniform Sampling的主要内容,如果未能解决你的问题,请参考以下文章