简单实用算法——二分查找法（BinarySearch）

Posted timefiles

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了简单实用算法——二分查找法（BinarySearch）相关的知识，希望对你有一定的参考价值。

目录

算法概述

二分查找（英语：binary search），也叫折半查找（英语：half-interval search），是一种在有序数组中查找特定元素的搜索算法。所以，二分查找的前提是数组必须是有序的。
时间复杂度、空间复杂度请参照下图（图片来自wikipedia）：
技术图片

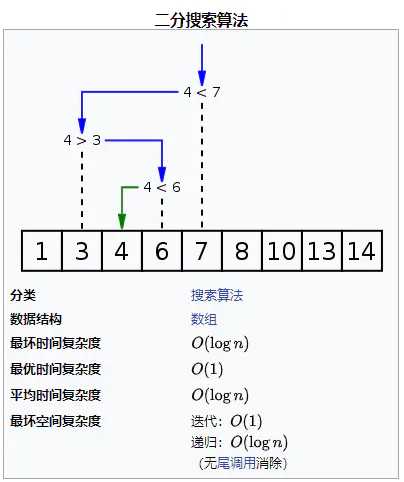
适用情况

二分查找只适用顺序存储结构。为保持表的有序性，在顺序结构里插入和删除都必须移动大量的结点。因此，二分查找特别适用于那种一经建立就很少改动、而又经常需要查找的线性表。

对那些查找少而又经常需要改动的线性表，可采用链表作存储结构，进行顺序查找。链表上无法实现二分查找（更准确的说链表上使用二分查找得不偿失）。

算法原理

二分查找的基本思想是：

  • 设R[low…..high]是当前的查找区间。
  • 首先确定该区间的中点位置：mid = low + ((high - low) >> 1)。
  • 然后将待查的target值与ary[mid]比较：若相等，则查找成功并返回此位置，否则须确定新的查找区间，继续二分查找。
  • 若ary[mid]>target，则由表的有序性可知ary[mid….high]均大于K，因此若表中存在关键字等于target的结点，则该结点必定是在位置mid左边的子表R[low…mid-1]中，故新的查找区间是左子表ary[low…...mid-1]。
  • 若ary[mid]<target，则要查找的target必在mid的右子表ary[mid+1……high]中，即新的查找区间是右子表ary[mid+1……high]。
  • 下一次查找是针对新的查找区间进行的。

因此，从初始的查找区间R[0..n-1]开始，每经过一次与当前查找区间的中点位置上的结点关键字的比较，就可确定查找是否成功，不成功则当前的查找区间就缩小一半。这一过程重复直至找到关键字为target的结点，或者直至当前的查找区间为空(high<low,即查找失败)时为止。

算法实现（C#）

算法基于C#编写，有简单和泛型两种实现，每种实现又分递归版本、While循环版本。实际运用时，推荐使用While循环版本的二分查找。
算法代码如下：

    //此算法假定数组已排序；如果不是这样，则结果将不正确。
    class BinarySearch
    {
        //不要使用mid = (high + low) / 2，可能会导致运算溢出
        #region 简单
        // 递归版本           
        public static int Recursive(int[] ary, int target)
        {
            return Recursive(ary, 0, ary.Length-1, target);           
        }
        static int Recursive(int[] ary, int low, int high, int target)
        {
            if (high < low) return -1;    
            int mid = low + ((high - low) >> 1);
            if (ary[mid] == target) return mid;
            if (ary[mid] > target)
            {
                return Recursive(ary, low, mid-1, target);
            }
            else
            {
                return Recursive(ary, mid + 1, high, target);
            }            
        }
        //While循环版本
        public static int WhileLoop(int[] ary, int target)
        {
            int low = 0; 
            int high = ary.Length - 1;
            while (low <= high)
            {                                
                int mid = low + ((high - low) >> 1);
                if (ary[mid] == target) return mid;
                if (ary[mid] > target)
                {
                    high = mid - 1;
                }
                else 
                {
                    low = mid + 1;
                }
            }
            return -1;
        }
        #endregion
        
        #region 泛型
        // 递归版本           
        public static int RecursiveT<T>(T[] ary, T target) where T : IComparable
        {
            return RecursiveT(ary, 0, ary.Length - 1, target);
        }
        static int RecursiveT<T>(T[] ary, int low, int high, T target) where T : IComparable
        {               
            if (high < low) return -1;            
            int mid = low + ((high - low) >> 1);
            int cr = Comparer.Default.Compare(ary[mid], target);             
            if(cr==0)return mid;
            if (cr > 0)
            {
                return RecursiveT(ary, low, mid - 1, target);
            }
            else 
            {
                return RecursiveT(ary, mid + 1, high, target);
            }            
        }
        //While循环版本
        public static int WhileLoopT<T>(T[] ary, T target) where T : IComparable
        {
            int low = 0;
            int high = ary.Length - 1;
            while (low <= high)
            {                
                int mid = low + ((high - low) >> 1);
                int cr = Comparer.Default.Compare(ary[mid], target);                
                if (cr == 0) return mid;
                if (cr>0)
                {
                    high = mid - 1;
                }
                else 
                {
                    low = mid + 1;
                }               
            }
            return -1;
        }
        //默认情况下推荐使用While循环版本
        public static int DefaultT<T>(T[] ary, T target) where T : IComparable 
        {            
            return WhileLoopT(ary, target);
        }
        #endregion 
    }

测试代码如下：

//数组必须有序
//此处用升序递增的整数数组是为了便于检查结果
int[] ary = new int[] { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20 }; 
long[] aryT = new long[] { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20 };            
int target = 8;
int r = BinarySearch.Recursive(ary, target);
int w = BinarySearch.WhileLoop(ary, target);
int rT = BinarySearch.RecursiveT(ary, target);
int wT = BinarySearch.WhileLoopT(ary, target);
Console.WriteLine("r={0} w={1} rT={2} wT={3}", r, w, rT, wT);

实际应用：用二分查找法找寻边界值

在集合中找到一个大于（小于）目标数t的数x，使得集合中的任意数要么大于（小于）等于x，要么小于（大于）等于t。
举例来说：给予数组和目标数

int array = {2, 3, 5, 7, 11, 13, 17};
int target = 7;

那么上界值应该是11，因为它“刚刚好”大于7；下界值则是5，因为它“刚刚好”小于7。

该问题不能直接使用二分查找的实现代码解决，需要对代码做一些修改，但解题思路还是二分查找。

实现代码如下：

//用二分查找法找寻上界
static int BSearchUpperBound(int[] ary, int target)
{           
    int low = 0;
    int high = ary.Length - 1;            
    while (low <= high)
    {
        int mid = low + ((high - low) >> 1);
        if (high == low) 
        {
            if (ary[mid] > target) return mid;
            else return -1;            
        }
        if (ary[mid] > target)
        {
            //当前找到的数大于目标数时，它可能就是我们要找的数，所以需要保留这个索引
            high = mid ;
        }
        else
        {
            //当前找到的数小于等于目标数时继续向上取区间
            low = mid + 1;
        }
    }
    return -1;        
}
 //用二分查找法找寻下界
static  int BSearchLowerBound(int[] ary, int target)
{
    int low = 0;
    int high = ary.Length - 1;
    while (low <= high)
    {
        //取中间索引时使用向上取整，否则low无法往上爬到下界值
        int mid = low + ((high - low + 1) >> 1);
        if (high == low)
        {
            if (ary[mid] < target) return mid;
            else return -1;
        }               
        if (ary[mid] >= target)
        {
            //当前找到的数大于等于目标数时继续向下取区间
            high = mid-1;
        }
        else
        {
            //当前找到的数小于目标数时，它可能就是我们要找的数，所以需要保留这个索引
            low = mid;
        }
    }
    return -1;
}

测试代码如下：

//寻找边界值
int[] array =new int[]{ 2, 3, 5, 7, 11, 13, 17 };
int target =6;
//用二分查找法找寻上届
int up = BSearchUpperBound(array, target);
int lo=BSearchLowerBound(array, target);

参考文章

二分搜索（Binary_Search）——简书
binary search——百度百科
BinarySearch——.NET源码
二分查找BinarySearch原理分析、判定树、及其变种——CSDN
二分查找法的实现和应用汇总——CSDN









以上是关于简单实用算法——二分查找法（BinarySearch）的主要内容，如果未能解决你的问题，请参考以下文章

每周算法小知识之二分查找

冒泡排序法与二分查找法

二分查找法和牛顿法求根号的实现

算法：二分查找法

Java二分查找算法复制粘贴直接用

分治法之二分查找