数据结构与算法（19）——快速排序

Posted 2020-12-18 yeshengcqupt

• 快速排序

思想：依据一个中值数据项，把数据表分成两半：小于中值的一半和大于中值的一半，然后把每部分分别进行快速排序(递归)。

其中递归条件：

基本结束条件：数据表仅有一个数据项

缩小规模：根据中值，将数据表分为两半，最好的情况是相等规模的两半

调用自身：将两半分别调用自身进行排序（排序基本操作在分裂过程中）

 

 

 

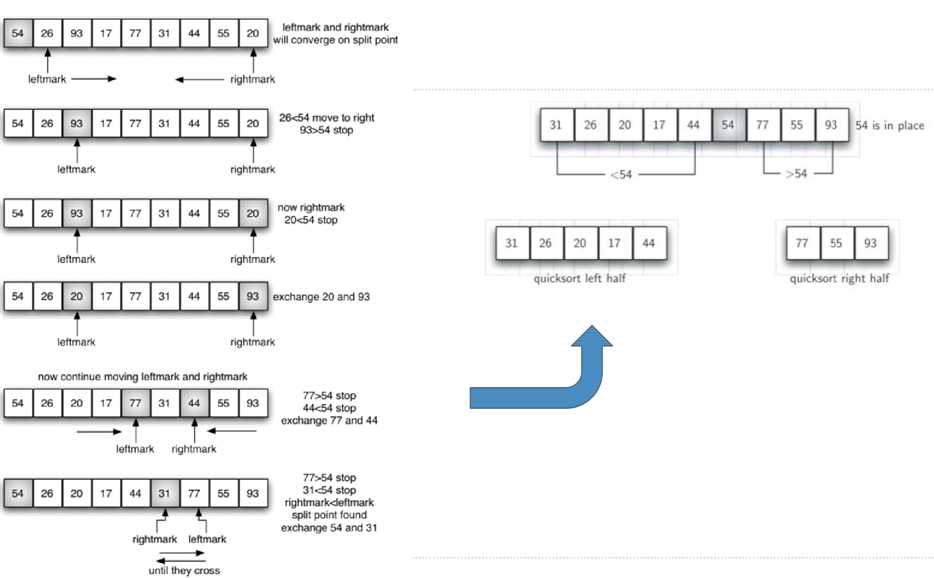
 快速排序的图解过程：

 

• 快速排序代码

def partition(alist, first, last):
    pivotvalue = alist[first] #以第一个数作为中值
    leftmark = first + 1
    rightmark = last

    done = False
    while not done:
        while leftmark <= rightmark and alist[leftmark] <= pivotvalue: #右移动左标
            leftmark += 1
        while alist[rightmark] >= pivotvalue and rightmark >= leftmark: #左移动右标
            rightmark -= 1
        if rightmark < leftmark: #两个数相错就结束移动
            done = True
        else: #左右值交换
            temp = alist[leftmark]
            alist[leftmark] = alist[rightmark]
            alist[rightmark] = temp
            #alist[leftmark], alist[rightmark] = alist[leftmark], alist[rightmark]
    temp = alist[first]
    alist[first] = alist[rightmark]
    alist[rightmark] = temp
    return rightmark

def quickSort(alist):
    quickerSortHelper(alist, 0, len(alist)-1)

def quickerSortHelper(alist, first, last):
    if first < last:
        splitpoint = partition(alist, first, last)
        quickerSortHelper(alist, first, splitpoint-1)
        quickerSortHelper(alist,splitpoint+1, last)
alist = [54, 26, 93, 17, 77, 31, 44, 55, 20]
quickSort(alist)
print(alist)

• 　　时间复杂度分析

快排包括分裂和移动两个部分：分裂的时间服大肚是O(n) ,移动O(log n)，总的时间复杂度为O(nlog n)，且不需要额外存储空间。

但是快排也有缺点，在极端情况，如果不幸，中值所在的分裂点过于偏离中部，造成左右两部分数据不平衡，且在有一部分始终没有数据的话，这样时间复杂度就退化到O(n^2)。

注意：中值的选取对排序十分重要，因此需要有先验知识对数据的特性选取合适的中值。