trie树（字典树）

Posted 2020-12-18 zhenglijie

Trie字符串统计

维护一个字符串集合，支持两种操作：

1. “I x”向集合中插入一个字符串x；
2. “Q x”询问一个字符串在集合中出现了多少次。

共有N个操作，输入的字符串总长度不超过 105105，字符串仅包含小写英文字母。

输入格式

第一行包含整数N，表示操作数。

接下来N行，每行包含一个操作指令，指令为”I x”或”Q x”中的一种。

输出格式

对于每个询问指令”Q x”，都要输出一个整数作为结果，表示x在集合中出现的次数。

每个结果占一行。

数据范围

1 ≤ N ≤ 2∗10^4

输入样例：

5
I abc
Q abc
Q ab
I ab
Q ab

输出样例：

1
0
1

 

Tire树就是用来快速储存和查找字符串集合的结构。

例如：我们构建一个Trie树 然后每到一个字符串的终点我们会做一个标记 当遍历到标记时就认为这个字符串存在于字典树中

看下图，我们给出字符串然后做出字典树

 

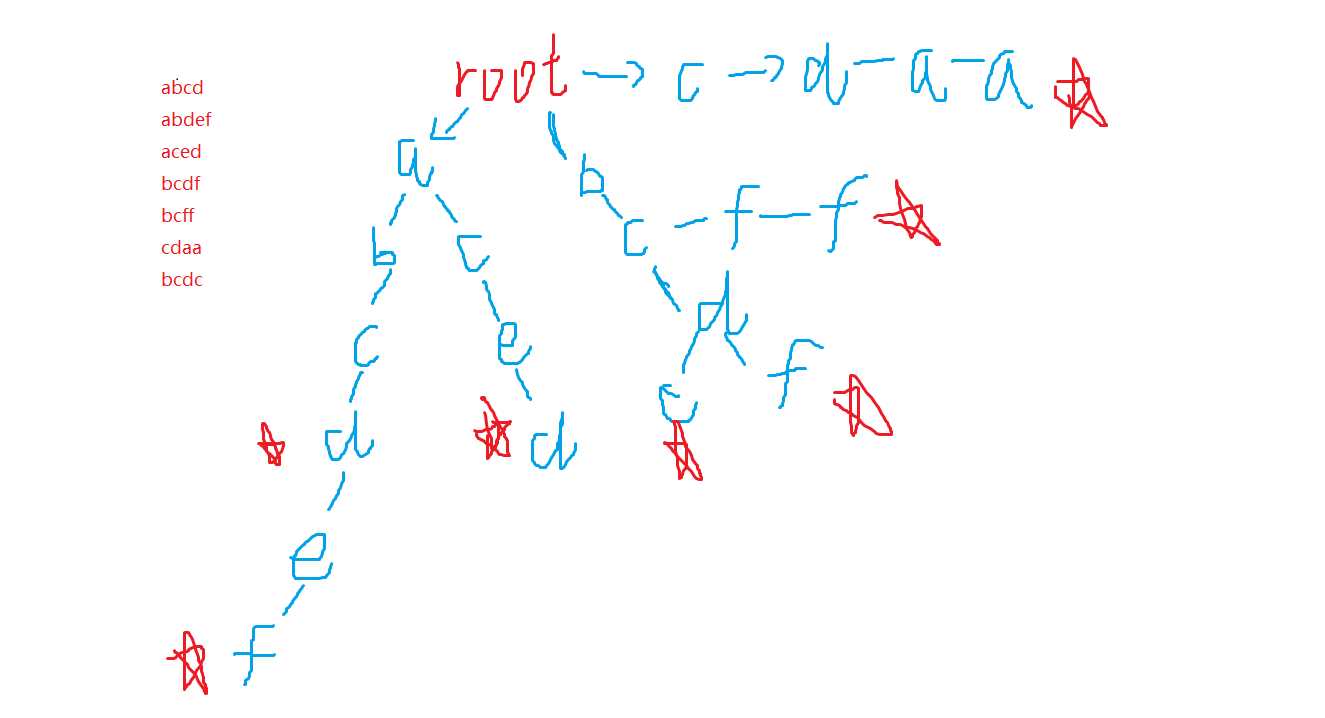
insert（插入操作）：

 p = 0 从根节点开始，我们开始遍历字符串，如果发现存在已有结点则p继续向下索引即： p = son[p][u] ，若不存在则我们建立结点，最后 cnt[p]++ ，表示插入完毕，因此插入代码。

 1 void insert(char *str)  //插入
 2 { 
 3     int p = 0;
 4     for(int i = 0; str[i]; i++)
 5     {
 6         int u = str[i]-‘a‘;
 7         if(!son[p][u]) son[p][u] = ++idx;  //没有直接存字母，而是占用下标 表示这个位置存在字母
 8         p = son[p][u];
 9     }
10 
11     cnt[p]++;
12 }

（query）查询操作：

依然是 p = 0 从根节点开始，若查找失败则直接返回，否则返回出现次数 return cnt[p]; 

 1 int query(char *str) //询问
 2 {
 3     int p = 0;  
 4     for(int i = 0; str[i]; i++)
 5     {
 6         int u = str[i]-‘a‘;
 7         if(!son[p][u]) return 0;
 8         p = son[p][u];
 9     }
10 
11     return cnt[p];
12 }

总代码：

 1 #include <iostream>
 2 
 3 using namespace std;
 4 
 5 const int N = 100010;
 6 
 7 int son[N][26], cnt[N], idx;
 8 char str[N];
 9 
10 void insert(char *str)  //插入
11 { 
12     int p = 0;
13     for(int i = 0; str[i]; i++)
14     {
15         int u = str[i]-‘a‘;
16         if(!son[p][u]) son[p][u] = ++idx;  //没有直接存字母，而是占用下标 表示这个位置存在字母
17         p = son[p][u];
18     }
19 
20     cnt[p]++;
21 }
22 
23 int query(char *str) //询问
24 {
25     int p = 0;  
26     for(int i = 0; str[i]; i++)
27     {
28         int u = str[i]-‘a‘;
29         if(!son[p][u]) return 0;
30         p = son[p][u];
31     }
32 
33     return cnt[p];
34 }
35 
36 int main()
37 {
38     int n;
39     scanf("%d", &n);
40     while(n--)
41     {
42         char op[2];
43         scanf("%s%s", op, str);
44         if(*op == ‘I‘) insert(str);
45         else printf("%d
", query(str));
46     }
47 
48     system("pause");
49     return 0;
50 }

 

最大异或对

在给定的N个整数A1，A2……AN中选出两个进行xor（异或）运算，得到的结果最大是多少？

输入格式

第一行输入一个整数N。

第二行输入N个整数A1～AN。

输出格式

输出一个整数表示答案。

数据范围

1 ≤ N ≤ 10^5,

0 ≤ Ai < 2^31

输入样例：

3

1 2 3

输出样例：

3

 

这道题可知，trie树不仅仅可以存字符串，还可以存数字的二进制数。

首先考虑暴力的做法

1 int res = 0;
2 for(int i = 0; i < n; i++)
3 {
4     int t = a[i];
5     for(int j = 0; j < i; j++)
6     {
7         res = max(res, t ^ a[j]);
8     }
9 }

因为防止出现类似于1 3，3 1 这样重复比较的出现 我们第二重循环就直接遍历到i，因此我们发现，n个数选两个数两两组合则一共有C²_n  种选法。

对于这道题的思路首先想：若要使得两数异或结果最大，则我们得从最高位开始考虑，假设：7与3，7与5

7：（111）₂

3：（011）₂

5：（101）₂

从最高位开始看，7与3最高位异或得1，7与5最高位异或得0，则得出结论，很显然7与3异或得到结果更大。

因此我们维护一个最大值即结果，可以先把7得二进制插入trie树，现在trie树中只有7，因此3就与7异或得到一个数，更新结果，然后把3插入trie树，然后再拿5与trie树中的元素进行运算，现在得trie树有两个元素，看图：

 

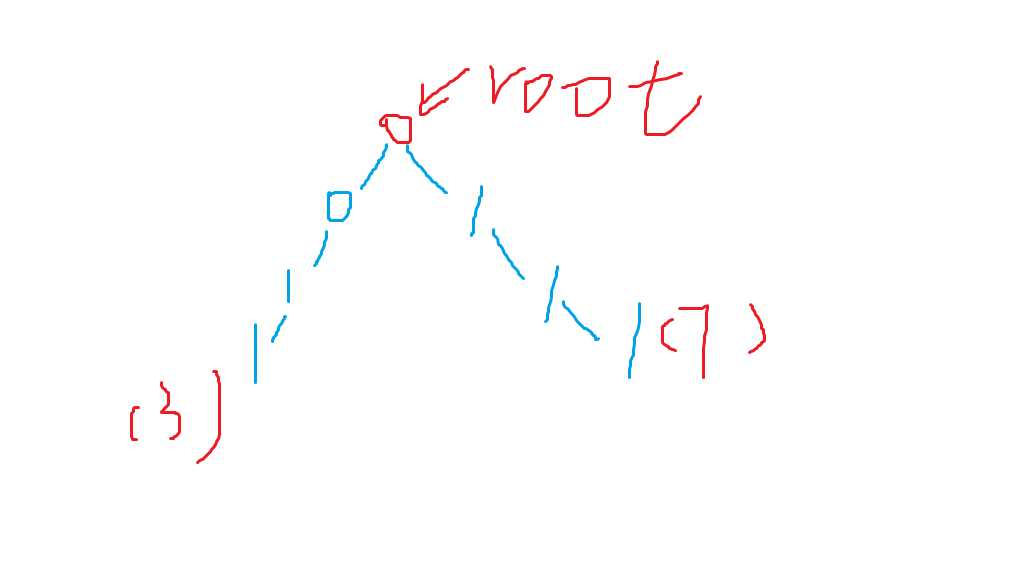
然后，很明显左边分支最高位是0， 右边分支最高位是1，则我们肯定选择走左边分支，因为1与0异或是1，然后5的第二位0 与 3的第二位1异或得1依然最大，然后5的最低位1与3的最低位1异或得0，但是我们没有别的分支了，所以体现在程序里就是要先判断与它当前位置数不同的分支是否存在，如果存在则走与它不同的那个分支，否则只能走与它相同的分支。

insert操作（同上）：

 1 void insert(int x)
 2 {
 3     int p = 0;
 4     for(int i = 30; i >= 0; i--)
 5     {
 6         int u = x >> i & 1;
 7         if(!son[p][u]) son[p][u] = ++idx;
 8         p = son[p][u];
 9     }
10 }

查询操作：

 1 int query(int x)
 2 {
 3     int p = 0, res = 0;  //返回异或后最大的数字结果
 4     for(int i = 30; i >= 0; i--)
 5     {
 6         int u = x >> i & 1;
 7         if(son[p][!u]) //如果发现与它不同的分支存在 则优先走与它不同的分支
 8         {
 9             p = son[p][!u];
10             res = res*2 + !u;
11         }
12         else 
13         {
14             p = son[p][u];
15             res = res*2 + u;
16         }
17     }
18 
19     return res;
20 }

总代码：

 1 #include <iostream>
 2 #include <algorithm>
 3 
 4 using namespace std;
 5 
 6 const int N = 100010, M = 31*N;
 7 int n;
 8 int a[N], son[M][2], idx;
 9 
10 void insert(int x)
11 {
12     int p = 0;
13     for(int i = 30; i >= 0; i--)
14     {
15         int u = x >> i & 1;
16         if(!son[p][u]) son[p][u] = ++idx;
17         p = son[p][u];
18     }
19 }
20 
21 int query(int x)
22 {
23     int p = 0, res = 0;  //返回异或后最大的数字结果
24     for(int i = 30; i >= 0; i--)
25     {
26         int u = x >> i & 1;
27         if(son[p][!u]) //如果发现与它不同的分支存在 则优先走与它不同的分支
28         {
29             p = son[p][!u];
30             res = res*2 + !u;
31         }
32         else 
33         {
34             p = son[p][u];
35             res = res*2 + u;
36         }
37     }
38 
39     return res;
40 }
41 
42 int main()
43 {
44     scanf("%d", &n);
45     for(int i = 0; i < n; i++) scanf("%d", &a[i]);
46 
47     int res = 0;
48     for(int i = 0; i < n; i++) //可以插入一个查询一个，也可以先插入所有再查询
49     {
50         insert(a[i]);
51         int t = query(a[i]);
52         res = max(res, a[i] ^ t);
53     }
54 
55     printf("%d
", res);
56 
57     system("pause");
58     return 0;
59 }