动态规划

Posted 2020-12-18 lgh544

1. 最长回文子串

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

示例 1：

输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。

示例 2：

输入: "cbbd"
输出: "bb"

动态规划
1、当 i 和 j 的差距等于小于 3 的时候，dp 值可以直接判断，不用参考以前的 dp 值；

2、其它情况，每当计算新 dp 值的时候，都一定会参考「左下角」的 dp 值，即 dp[i + 1][j - 1]（i + 1 表示在下边，j - 1 表示在左边）。

因此，从上到下写，或者从下到上写，都是可以的。

下面分别展示了错误的填表顺序和正确的填表顺序，以便大家理解动态规划要满足「无后效性」的意思。

复杂度分析：

    时间复杂度：O(N2)。
    空间复杂度：O(N2)，二维 dp 问题，一个状态得用二维有序数对表示，因此空间复杂度是 O(N2)

class Solution {
    public String longestPalindrome(String s) {
        int len =s.length();
        if(len<2)return s;

       boolean[][] dp=new boolean[len][len];
       for(int i=0;i<len;i++){
           Arrays.fill(dp[i],false);
       }
       for(int i=0;i<len;i++){
           dp[i][i]=true;
       }
       int maxlen=1;
       int start=0;
       char[] c=s.toCharArray();

       for(int j=1;j<len;j++){
           for(int i=0;i<j;i++){
               //aba的时候j-i<3 ,c[0]==c[2],此时就不需要再判断dp[i+1][j-1]
               dp[i][j]=(c[i]==c[j])&&(j-i<3||dp[i+1][j-1]);

               if(dp[i][j]){
                   int curlen=j-i+1;
                   if(maxlen<curlen){
                       maxlen=curlen;
                       start=i;
                   }
               }
           }
       }
       return s.substring(start,start+maxlen);
    }
}

 

2. 编辑距离

给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

1. 插入一个字符
2. 删除一个字符
3. 替换一个字符

 

示例 1：

输入：word1 = "horse", word2 = "ros"
输出：3
解释：
horse -> rorse (将 ‘h‘ 替换为 ‘r‘)
rorse -> rose (删除 ‘r‘)
rose -> ros (删除 ‘e‘)

示例 2：

输入：word1 = "intention", word2 = "execution"
输出：5
解释：
intention -> inention (删除 ‘t‘)
inention -> enention (将 ‘i‘ 替换为 ‘e‘)
enention -> exention (将 ‘n‘ 替换为 ‘x‘)
exention -> exection (将 ‘n‘ 替换为 ‘c‘)
exection -> execution (插入 ‘u‘)

动态规划：

dp[i][j] 代表 word1 到 i 位置转换成 word2 到 j 位置需要最少步数

所以，

当 word1[i] == word2[j]，dp[i][j] = dp[i-1][j-1]；

当 word1[i] != word2[j]，dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1

其中，dp[i-1][j-1] 表示替换操作，dp[i-1][j] 表示删除操作，dp[i][j-1] 表示插入操作。

注意，针对第一行，第一列要单独考虑，我们引入 ‘‘ 下图所示：

 

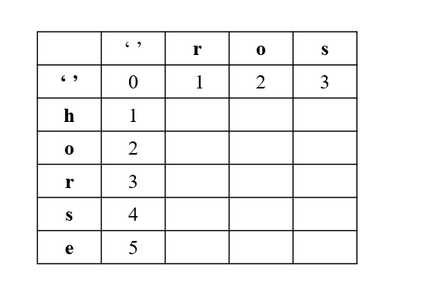
 第一行，是 word1 为空变成 word2 最少步数，就是插入操作

第一列，是 word2 为空，需要的最少步数，就是删除操作

再附上自顶向下的方法，大家可以提供 Java 版吗？

class Solution {
    public int minDistance(String word1, String word2) {
        int n1=word1.length();
        int n2=word2.length();
        int[][] dp=new int[n1+1][n2+1];
        for(int j=1;j<=n2;j++){
            dp[0][j]=dp[0][j-1]+1;
        }
         for(int j=1;j<=n1;j++){
            dp[j][0]=dp[j-1][0]+1;
        }
        for(int i=1;i<=n1;i++){
            for(int j=1;j<=n2;j++){
                if(word1.charAt(i-1)==word2.charAt(j-1)){
                    dp[i][j]=dp[i-1][j-1];
                }else{
                    dp[i][j]=Math.min(Math.min(dp[i-1][j-1],dp[i-1][j]),dp[i][j-1])+1;
                }
            }
        }
        return dp[n1][n2];
    }
}