有约束的非线性规划的求解

Posted 2020-12-17 noturns

标准形式：

[minquad f(x)s.t.egin{cases} G_1(x)leq 0,G_2(x)=0quad (非线性约束)AXleq b,Aeqcdot X=beqquad (线性约束)vlbleq Xleq vubquad (决策变量的范围约束)end{cases} ]

调用 fmincon() 函数：

[x,favl]=fmincon(@fun,x0,A,b,Aeq,beq,vlb,vub,@con)

求解流程：

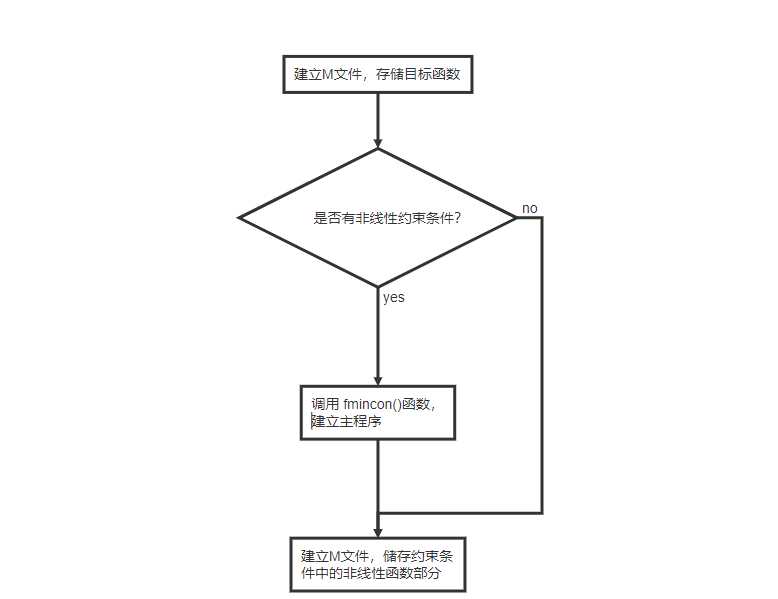
例：

[maxquad f(x)=x_1^2+x^2_2-x_1x_2-2x_1-5x_2s.t.egin{cases} -(x_1-1)^2+x_2geq 02x_1-3x_2+6geq 0初始值：x_1=0,x_2=1 end{cases} ]

转化为标准形式：

[minquad f(x)=-x_1^2-x^2_2+x_1x_2+2x_1+5x_2s.t.egin{cases} (x_1-1)^2-x_2leq 0-2x_1+3x_2-6leq 0初始值：x_1=0,x_2=1 end{cases} ]

①：

function f=fun(x)
f=-x(1)^2-x(2)^2+x(1)*x(2)+2*x(1)+5*x(2);
end

②

function [G,Geq]=cont(x)
G=(x(1)-1)^2-x(2);
Geq=[];
end

③

x0=[0 1];
A=[-2,3];
b=6;
Aeq=[];
beq=[];
lb=[];
ub=[];
[x,favl]=fmincon(@fun,x0,A,b,Aeq,beq,lb,ub,@cont)

运行结果可知，最大值为-1：

x =

    1.0000    0.0000


favl =

    1.0000

>>