[WC2009]最短路问题 题解

Posted 2020-12-17 verjun

题意

给定一个$6 imes n$的方格，每个点有一个非负权值，有两种操作

• 给定$x,y,c$，表示将坐标为$(x,y)$的格子的权值改为$c$
• 给定$x_1,y_1,x_2,y_2$，求出从$(x_1,y_1)$到$(x_2,y_2)$的最短路

$nle 10^5$

Sol

打表枚举观察可得，最终路径由最多$3$步组成

• 从起点向右走一圈，再向左走一圈，最后回到$x$所在直线（可省略）

 

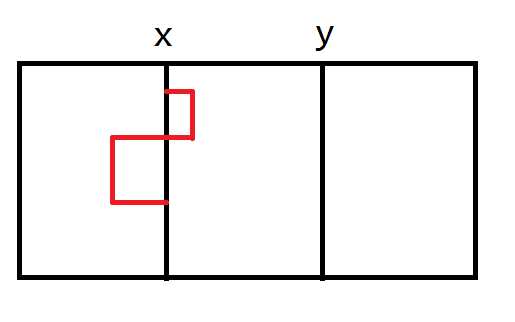
• 从$x$所在直线走到$y$所在直线

 

 

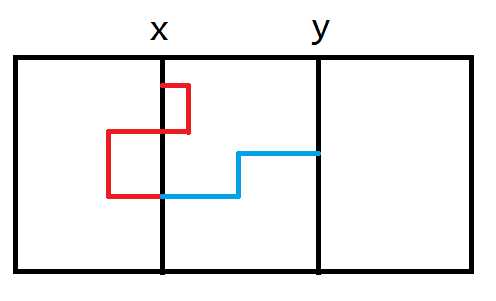
• 从$y$所在直线向右走一圈，再向左走一圈，最后到终点（可省略）

 

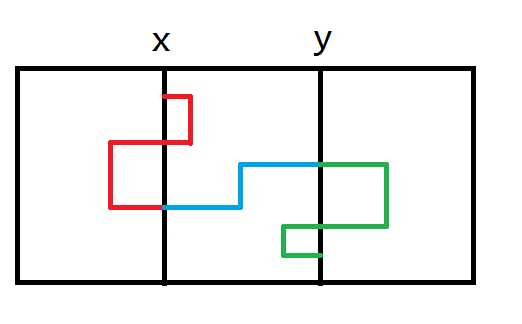
所需数组

所以我们需要记录一些$6 imes6$的矩阵，令当前处理区间为$[l,r]$，区间中点为$mid$：

强调：所有路径均为左开右闭

• $ll[i][j]$代表在内部从点$(i,l)$到点$(j,l)$的最短路，如下图所示：

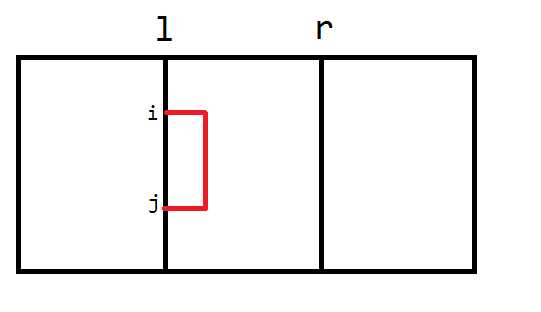
• $lr[i][j]$代表在内部从点$(i,l)$到点$(j,r)$的最短路，如下图所示：

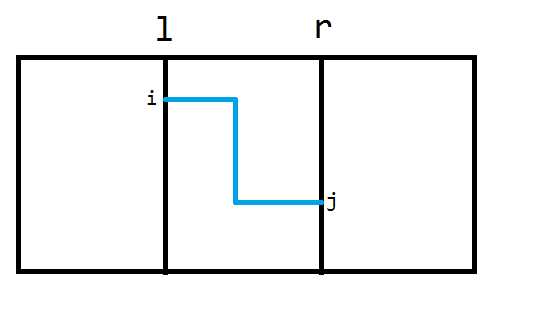
• $rr[i][j]$代表在内部从点$(i,r)$到点$(j,r)$的最短路，如下图所示：

 

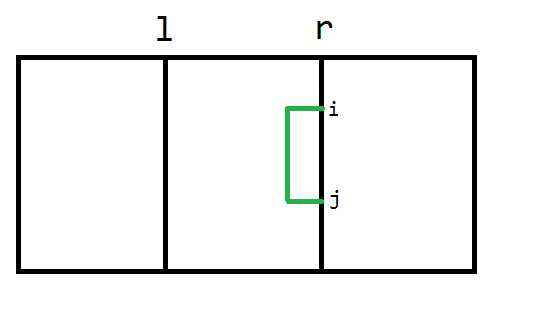
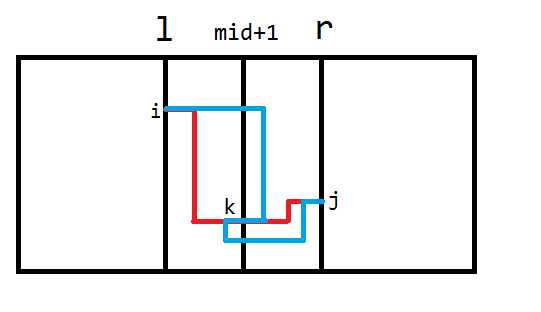
• $lm[i][j]$代表从$(i,l)$到$(j,mid)$的必须经过$mid$右边的最短路，如下图所示

 

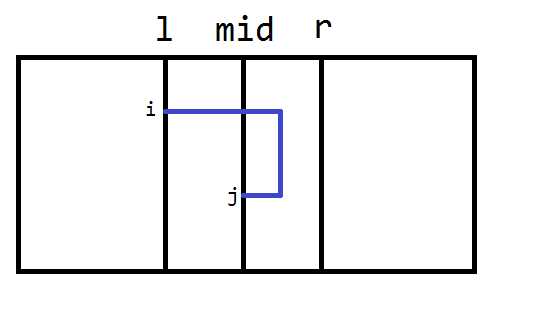
• $rm[i][j]$表示从$(i,mid+1)$到点$(j,r)$的必须经过$mid$左边的最短路，如下图所示

 

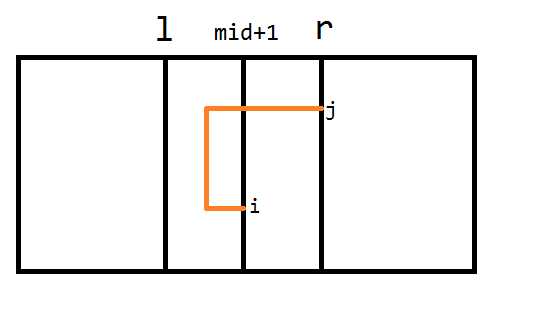
 上传操作

区间信息的维护可以用线段树处理，考虑上传操作：

枚举$kin[1,6]$，令$ls$为左儿子，$rs$为右儿子，不难推出

$$lm[i][j] = min{ls.lr[i][k]+rs.ll[k][j]+ls.rr[j][j]}$$

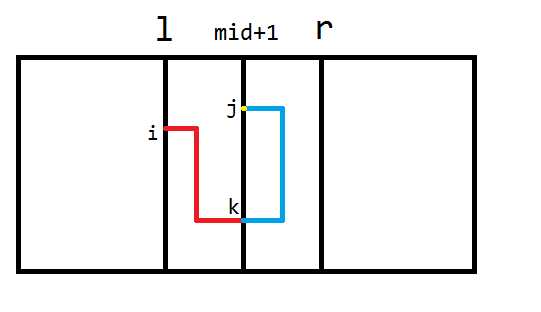
$$rm[i][j]=min{ls.rr[i][k]+rs.lr[k][j]+rs.ll[j][j]}$$

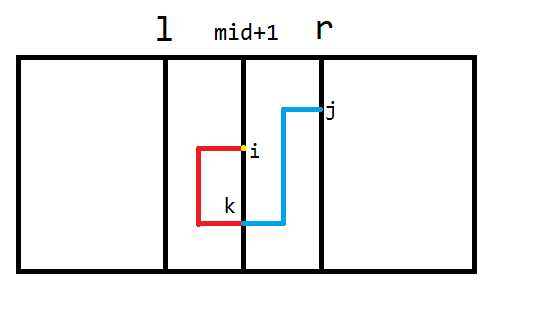
$$ll[i][j]=min{ls.ll[i][j],lm[i][k]+ls.lr[j][k]-ls.rr[k][k]}$$

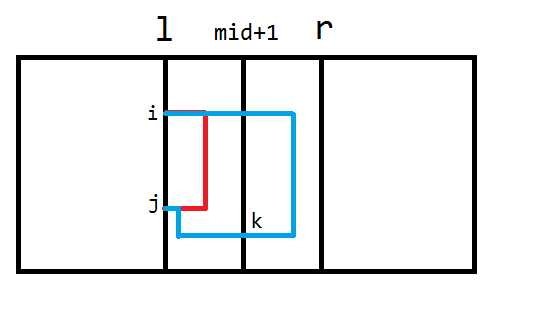
$$rr[i][j]=min{rs.rr[i][j],rm[k][i]+rs.lr[k][j]-rs.ll[k][k]}$$

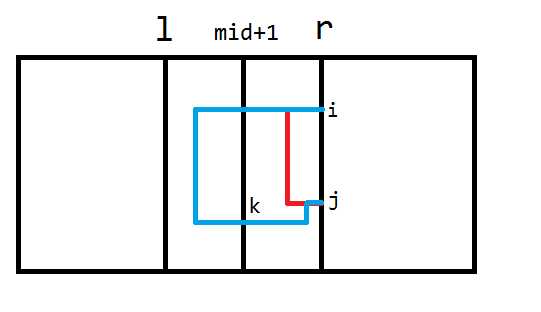
$$lr[i][j]=min{lm[i][k]+rm[k][j]-ls.rr[k][k]-rs.ll[k][k],ls.lr[i][k]+rs.lr[k][j]}$$

统计答案

可能的路径有$4$中情况（此处的$1,2,3$代表上面的三步）

令$ls=[1,y_1),mid=[y_1,y_2],rs=(y_2,n]$，枚举$i,j$

• 只有$2$  $$ans = mid.lr[x_1][x_2]$$
• 有$1,2$  $$ans=min{mid.ll[x_1][i]+ls.rr[i][j]+mid.lr[j][x_2]-val[i][y_1]-val[j][y_1]}$$
• 有$2,3$ $$ans=min{mid.lr[x_1][i]+rs.ll[i][j]+mid.rr[j][x_2]-val[i][y_2]-val[j][y_2]$$
• 有$1,2,3$  $$ans=min{ls.rr[x_1][i]+mid.lr[i][j]+rs.ll[j][x_2]-val[i][y_1]-val[j][y_2]}$$

将$4$种情况的$ans$取最小值即可。

#include <bits/stdc++.h>
#define inf 2139062143
using namespace std;
int Read() {
    int x = 0, f = 1;
    char ch = getchar();
    while (!isdigit(ch)) {
        if (ch == ‘-‘)
            f = -1;
        ch = getchar();
    }
    while (isdigit(ch)) {
        x = (x << 3) + (x << 1) + ch - ‘0‘;
        ch = getchar();
    }
    return x * f;
}
int n, a[7][100005];
struct node {
    int ll[7][7], rr[7][7], lr[7][7];
    void Clear() {
        memset(ll, 0x7f, sizeof(ll));
        memset(rr, 0x7f, sizeof(rr));
        memset(lr, 0x7f, sizeof(lr));
    }
    bool Empty() const { return ll[0][0] == inf; }
} seg[400005];
node operator+(const node &ls, const node &rs) {
    int lm[7][7], rm[7][7];
    if (ls.Empty())
        return rs;
    if (rs.Empty())
        return ls;
    node a;
    a.Clear();
    memset(lm, 0x7f, sizeof(lm));
    memset(rm, 0x7f, sizeof(rm));
    for (int k = 0; k < 6; k++) {
        for (int i = 0; i < 6; i++) {
            for (int j = 0; j < 6; j++) {
                lm[i][j] = min(lm[i][j], ls.lr[i][k] + rs.ll[k][j] + ls.rr[j][j]);
                rm[i][j] = min(rm[i][j], rs.ll[i][i] + ls.rr[i][k] + rs.lr[k][j]);
            }
        }
    }
    for (int i = 0; i < 6; i++) {
        for (int j = 0; j < 6; j++) {
            a.ll[i][j] = ls.ll[i][j], a.rr[i][j] = rs.rr[i][j], a.lr[i][j] = inf;
            for (int k = 0; k < 6; k++) {
                a.ll[i][j] = min(a.ll[i][j], lm[i][k] + ls.lr[j][k] - ls.rr[k][k]);
                a.rr[i][j] = min(a.rr[i][j], rm[k][i] + rs.lr[k][j] - rs.ll[k][k]);
                a.lr[i][j] = min(a.lr[i][j], ls.lr[i][k] + rs.lr[k][j]);
                a.lr[i][j] = min(a.lr[i][j], lm[i][k] + rm[k][j] - ls.rr[k][k] - rs.ll[k][k]);
            }
        }
    }
    return a;
}
void Init(int o, int l) {
    int sum[7];
    for (int i = 0; i < 6; i++) {
        sum[i] = (i ? sum[i - 1] : 0) + a[i][l];
    }
    for (int i = 0; i < 6; i++) {
        for (int j = 0; j < 6; j++) {
            int tmp = sum[max(i, j)] - (min(j, i) ? sum[min(j, i) - 1] : 0);
            seg[o].ll[i][j] = seg[o].rr[i][j] = seg[o].lr[i][j] = tmp;
        }
    }
}
void build(int o, int l, int r) {
    if (l == r) {
        Init(o, l);
        return;
    }
    int mid = (l + r) >> 1;
    build(o << 1, l, mid);
    build(o << 1 | 1, mid + 1, r);
    seg[o] = seg[o << 1] + seg[o << 1 | 1];
}
void modify(int o, int l, int r, int pos) {
    if (l == r) {
        Init(o, l);
        return;
    }
    int mid = (l + r) >> 1;
    if (pos <= mid)
        modify(o << 1, l, mid, pos);
    else
        modify(o << 1 | 1, mid + 1, r, pos);
    seg[o] = seg[o << 1] + seg[o << 1 | 1];
}
node query(int o, int l, int r, int nl, int nr) {
    if (nl <= l && r <= nr) {
        return seg[o];
    }
    node ans;
    ans.Clear();
    int mid = (l + r) >> 1;
    if (nl <= mid)
        ans = ans + query(o << 1, l, mid, nl, nr);
    if (mid < nr)
        ans = ans + query(o << 1 | 1, mid + 1, r, nl, nr);
    return ans;
}
int Qmin(int sx, int sy, int tx, int ty) {
    node ls = query(1, 1, n, 1, sy);
    node md = query(1, 1, n, sy, ty);
    node rs = query(1, 1, n, ty, n);
    int ans = md.lr[sx][tx];
    for (int i = 0; i < 6; i++) {
        for (int j = 0; j < 6; j++) {
            ans = min(ans, md.ll[sx][i] + ls.rr[i][j] + md.lr[j][tx] - a[i][sy] - a[j][sy]);
            ans = min(ans, md.lr[sx][i] + rs.ll[i][j] + md.rr[j][tx] - a[i][ty] - a[j][ty]);
            ans = min(ans, ls.rr[sx][i] + md.lr[i][j] + rs.ll[j][tx] - a[i][sy] - a[j][ty]);
        }
    }
    return ans;
}
int main() {
    n = Read();
    for (int i = 0; i < 6; i++) {
        for (int j = 1; j <= n; j++) {
            a[i][j] = Read();
        }
    }
    build(1, 1, n);
    int m = Read();
    for (int i = 1; i <= m; i++) {
        int opt = Read();
        if (opt == 1) {
            int x = Read(), y = Read(), z = Read();
            a[x - 1][y] = z;
            modify(1, 1, n, y);
        } else {
            int x = Read(), y = Read(), z = Read(), w = Read();
            if (y > w)
                swap(x, z), swap(y, w);
            printf("%d
", Qmin(x - 1, y, z - 1, w));
        }
    }
}

View Code