二维树状数组及(不会用到的)三维树状数组
Posted jasony
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了二维树状数组及(不会用到的)三维树状数组相关的知识,希望对你有一定的参考价值。
二维树状数组及(不会用到的)三维树状数组
前置芝士
一维树状数组(lowbit)
二维树状数组
二维树状数组涉及到两种基本操作,修改矩阵中的一个点,查询子矩阵的和
首先是修改点的操作:
void update(int x,int y,int z){ //坐标为(x,y)的点增加z
for(int i=x;i<=n;i+=lowbit(i))
for(int j=y;j<=n;j+=lowbit(j))
c[i][j]+=z;
}
然后是查询子矩阵的和,这里查询的是从左上角到目标点所形成的矩阵的元素和
int sum(int x,int y){
int ret=0;
for(int i=x;i>=1;i-=lowbit(i))
for(int j=y;j>=1;j-=lowbit(j))
ret+=c[i][j];
return ret;
}
那么如果我要查具体的一个子矩阵,就需要给出左上角的点和右下角的点的坐标,然后:
int x1,y1,x2,y2;
cin>>x1>>y1>>x2>>y2;
cout<<sum(x2,y2)-sum(x1-1,y2)-sum(x2,y1-1)+sum(x1-1,y1-1)<<endl;
就可以了
下面附上完整的二维树状数组的代码:
#include<iostream>
using namespace std;
const int maxn=1005;
const int maxm=1005;
int n,m;
int q;
int a[maxn][maxm];
int c[maxn][maxm];
int lowbit(int x)
{
return x&(-x);
}
void update(int x,int y,int z)
{
for(int i=x;i<=n;i+=lowbit(i))
for(int j=y;j<=m;j+=lowbit(j))
c[i][j]+=z;
}
int sum(int x,int y)
{
int ret=0;
for(int i=x;i>=1;i-=lowbit(i))
for(int j=y;j>=1;j-=lowbit(j))
ret+=c[i][j];
return ret;
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
cin>>a[i][j];
update(i,j,a[i][j]);
}
cin>>q;
while(q--)
{
int x;
cin>>x;
if(x==1)
{
int y,z,w;
cin>>y>>z>>w;
update(y,z,w);
}
if(x==2)
{
int x1,y1,x2,y2;
cin>>x1>>y1>>x2>>y2;
cout<<sum(x2,y2)-sum(x1-1,y2)-sum(x2,y1-1)+sum(x1-1,y1-1)<<endl;
}
}
return 0;
}
接下来我们对二维树状数组进行简单的拓展,将其拓展为修改矩形区间,查询单点的二维树状数组
其实就是把二维差分的思想引入进去,当然,如果不用树状数组直接用二维差分数组也是完全可以的,这个时候修改区间变成了O(1),查询点就变成了O(n),还是需要自己去权衡
二维树状数组的修改和查询的函数还是完全不用去变的
修改区间就要这么修改了:
void add(int x1,int y1,int x2,int y2,int w)
{
update(x1,y1,w);
update(x2+1,y2+1,w);
update(x2+1,y1,-w);
update(x1,y2+1,-w);
}
这个东西虽然是类比一维情况得来的,但是你不要去想,去在纸上画一画,主对角线端点为正,负对角线端点为负,然后就很显然了
查询单点的话直接sum(x,y)即可
这里给出完整的代码:
#include<iostream>
using namespace std;
const int maxn=1005;
const int maxm=1005;
int n,m;
int q;
int a[maxn][maxm];
int d[maxn][maxm];
int lowbit(int x)
{
return x&(-x);
}
void update(int x,int y,int z)
{
for(int i=x;i<=n;i+=lowbit(i))
for(int j=y;j<=m;j+=lowbit(j))
d[i][j]+=z;
}
void add(int x1,int y1,int x2,int y2,int w)
{
update(x1,y1,w);
update(x2+1,y2+1,w);
update(x2+1,y1,-w);
update(x1,y2+1,-w);
}
int sum(int x,int y)
{
int ret=0;
for(int i=x;i>=1;i-=lowbit(i))
for(int j=y;j>=1;j-=lowbit(j))
ret+=d[i][j];
return ret;
}
int main()
{
cin>>n>>m;
cin>>q;
while(q--)
{
int x;
cin>>x;
if(x==1)
{
int x1,y1,x2,y2,w;
cin>>x1>>y1>>x2>>y2>>w;
add(x1,y1,x2,y2,w);
}
if(x==2)
{
int x,y;
cin>>x>>y;
cout<<sum(x,y)<<endl;
}
}
return 0;
}
最后思考如何区间修改+区间查询
类比之前一维数组的区间修改区间查询(这个博客没有),下面这个式子表示的是点(x, y)的二维前缀和:
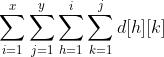
类比一维数组,统计一下每个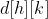 出现过多少次。
出现过多少次。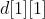 出现了
出现了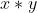 次,
次,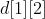 出现了
出现了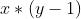 次……
次……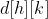 出现了
出现了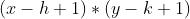 次。
次。
那么这个式子就可以写成:
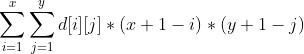
把这个式子展开,就得到:
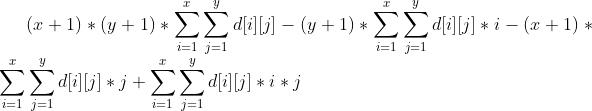
那么我们要开四个树状数组,分别维护:
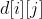 ,
, ,
, ,
,
这样就可以解决上述问题了
代码如下:
void update(int x,int y,int z)
{
for(int i=x;i<=n;i+=lowbit(i))
for(int j=y;j<=m;j+=lowbit(j))
d1[i][j]+=z;
d2[i][j]+=z*x;
d3[i][j]+=z*y;
d4[i][j]+=z*x*y;
}
void add(int x1,int y1,int x2,int y2,int w)
{
update(x1,y1,w);
update(x2+1,y2+1,w);
update(x2+1,y1,-w);
update(x1,y2+1,-w);
}
int sum(int x,int y)
{
int ret=0;
for(int i=x;i>=1;i-=lowbit(i))
for(int j=y;j>=1;j-=lowbit(j))
ret+=(x+1)*(y+1)*d1[i][j]-(y+1)*d2[i][j]-(x+1)*d3[i][j]+d4[i][j];
return ret;
}
int ask(int x1,int y1,int x2,int y2)
{
return sum(x2,y2)-sum(x2,y1-1)-sum(x1-1,y2)+sum(x1-1,y1-1);
}
模板题
BZOJ 3132(自己上网搜吧)
代码
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<string>
#include<cstring>
using namespace std;
const int maxn=2105;
const int maxm=2105;
int n,m;
int a[maxn][maxm],d1[maxn][maxm],d2[maxn][maxm],d3[maxn][maxm],d4[maxn][maxm];
int lowbit(int x)
{
return x&(-x);
}
void update(int x,int y,int z)
{
for(int i=x;i<=n;i+=lowbit(i))
for(int j=y;j<=m;j+=lowbit(j)){
d1[i][j]+=z;
d2[i][j]+=z*x;
d3[i][j]+=z*y;
d4[i][j]+=z*x*y;
}
}
void add(int x1,int y1,int x2,int y2,int w)
{
update(x1,y1,w);
update(x2+1,y2+1,w);
update(x2+1,y1,-w);
update(x1,y2+1,-w);
}
int sum(int x,int y)
{
int ret=0;
for(int i=x;i>=1;i-=lowbit(i))
for(int j=y;j>=1;j-=lowbit(j))
ret+=(x+1)*(y+1)*d1[i][j]-(y+1)*d2[i][j]-(x+1)*d3[i][j]+d4[i][j];
return ret;
}
int ask(int x1,int y1,int x2,int y2)
{
return sum(x2,y2)-sum(x2,y1-1)-sum(x1-1,y2)+sum(x1-1,y1-1);
}
int main()
{
char op[2];
scanf("%s",op);
cin>>n>>m;
while(scanf("%s",op)!=-1)
{
if(op[0]==‘L‘)
{
int x1,y1,x2,y2,w;
cin>>x1>>y1>>x2>>y2>>w;
add(x1,y1,x2,y2,w);
}
else
{
int x1,y1,x2,y2;
cin>>x1>>y1>>x2>>y2;
cout<<ask(x1,y1,x2,y2)<<endl;
}
}
return 0;
}
三维树状数组
怎么拓展呢?直接在二维树状数组的基础上加一维就可以了,不用进行任何改动,这里我们只介绍其中的一种变式,那就是三维树状数组修改区间查询点
(如果有人出三维树状数组修改区间查询区间的那种题,直接在二维树状数组修改区间查询区间的基础上改,应该不会有这种题的)
下面给出代码,着重观察修改部分就可以了。
#include<iostream>
using namespace std;
const int maxn=105;
const int maxm=105;
const int maxl=105;
int n,m,l;
int q;
int a[maxn][maxm][maxl];
int c[maxn][maxm][maxl];
int lowbit(int x)
{
return x&(-x);
}
void update(int x,int y,int z,int w)
{
for(int i=x;i<=n;i+=lowbit(i))
for(int j=y;j<=m;j+=lowbit(j))
for(int k=z;k<=l;k+=lowbit(k))
c[i][j][k]+=w;
}
int sum(int x,int y,int z)
{
int ret=0;
for(int i=x;i>=1;i-=lowbit(i))
for(int j=y;j>=1;j-=lowbit(j))
for(int k=z;k>=1;k-=lowbit(k))
ret+=c[i][j][k];
return ret;
}
int main()
{
cin>>n>>m>>l;
cin>>q;
while(q--)
{
int x;
cin>>x;
if(x==1)
{
int x1,y1,z1,x2,y2,z2,w;
cin>>x1>>y1>>z1>>x2>>y2>>z2>>w;
update(x1,y1,z1,w);
update(x1,y2+1,z1,-w);
update(x2+1,y1,z1,-w);
update(x2+1,y2+1,z1,w);
update(x1,y1,z2+1,-w);
update(x1,y2+1,z2+1,w);
update(x2+1,y1,z2+1,w);
update(x2+1,y2+1,z2+1,-w);
}
if(x==2)
{
int x,y,z;
cin>>x>>y>>z;
cout<<sum(x,y,z)<<endl;
}
}
return 0;
}
部分段落来自静听风吟。和Lv1_kangdi
以上是关于二维树状数组及(不会用到的)三维树状数组的主要内容,如果未能解决你的问题,请参考以下文章