K-近邻算法

Posted 2020-12-17 catxjd

一、概述

k-近邻算法（k-Nearest Neighbour algorithm），又称为KNN算法，是数据挖掘技术中原理最简单的算法。KNN 的工作原理：给定一个已知标签类别的训练数据集，输入没有标签的新数据后，在训练数据集中找到与新数据最邻 近的k个实例，如果这k个实例的多数属于某个类别，那么新数据就属于这个类别。可以简单理解为：由那些离X最 近的k个点来投票决定X归为哪一类。

　　　　　　　　　　

 

 

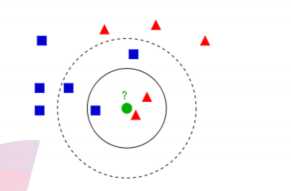
 图1 图1中有红色三角和蓝色方块两种类别，我们现在需要判断绿色圆点属于哪种类别

当k=3时，绿色圆点属于红色三角这种类别；

当k=5时，绿色圆点属于蓝色方块这种类别。

举个简单的例子，可以用k-近邻算法分类一个电影是爱情片还是动作片。（打斗镜头和接吻镜头数量为虚构）

电影名称	打斗镜头	接吻镜头	电影类型
无问西东	1	101	爱情片
后来的我们	5	89	爱情片
前任3	12	97	爱情片
红海行动	108	5	动作片
唐人街探案	112	9	动作片
战狼2	115	8	动作片
新电影	24	67	？

表1 每部电影的打斗镜头数、接吻镜头数和电影分类

表1就是我们已有的数据集合，也就是训练样本集。这个数据集有两个特征——打斗镜头数和接吻镜头数。除此之 外，我们也知道每部电影的所属类型，即分类标签。粗略看来，接吻镜头多的就是爱情片，打斗镜头多的就是动作 片。以我们多年的经验来看，这个分类还算合理。如果现在给我一部新的电影，告诉我电影中的打斗镜头和接吻镜 头分别是多少，那么我可以根据你给出的信息进行判断，这部电影是属于爱情片还是动作片。而k-近邻算法也可以 像我们人一样做到这一点。但是，这仅仅是两个特征，如果把特征扩大到N个呢？我们人类还能凭经验“一眼看 出”电影的所属类别吗？想想就知道这是一个非常困难的事情，但算法可以，这就是算法的魅力所在。

我们已经知道k-近邻算法的工作原理，根据特征比较，然后提取样本集中特征最相似数据（最近邻）的分类标签。 那么如何进行比较呢？比如表1中新出的电影，我们该如何判断他所属的电影类别呢？如图2所示。

 

 

 

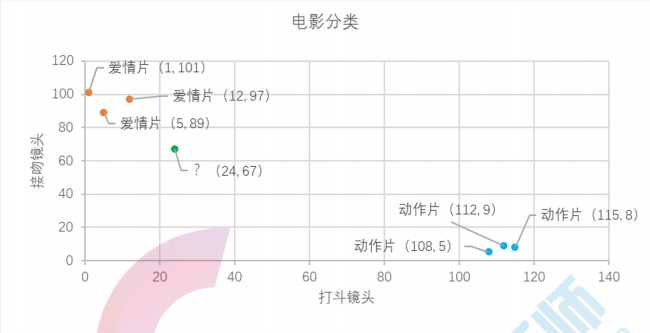
图2 电影分类 我们可以从散点图中大致推断，这个未知电影有可能是爱情片，因为看起来距离已知的三个爱情片更近一点。k-近 邻算法是用什么方法进行判断呢？没错，就是距离度量。这个电影分类例子中有两个特征，也就是在二维平面中计 算两点之间的距离，就可以用我们高中学过的距离计算公式：

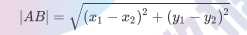
如果是多个特征扩展到N维空间，怎么计算？没错，我们可以使用欧氏距离（也称欧几里得度量），如下所示

 

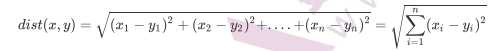
通过计算可以得到训练集中所有电影与未知电影的距离，如表2所示

 

电影名称	与未知电影的距离
无问西东	41.0
后来的我们	29.1
前任3	32.3
红海行动	104.4
唐人街探案	105.4
战狼2	108.5

通过表2的计算结果，我们可以知道绿点标记的电影到爱情片《后来的我们》距离最近，为29.1。如果仅仅根据这 个结果，判定绿点电影的类别为爱情片，这个算法叫做最近邻算法，而非k-近邻算法。k-近邻算法步骤如下：

(1) 计算已知类别数据集中的点与当前点之间的距离；

(2) 按照距离递增次序排序；

(3) 选取与当前点距离最小的k个点；

(4) 确定前k个点所在类别的出现频率；

(5) 返回前k个点出现频率最高的类别作为当前点的预测类别。

比如，现在K=4，那么在这个电影例子中，把距离按照升序排列，距离绿点电影最近的前4个的电影分别是《后来 的我们》、《前任3》、《无问西东》和《红海行动》，这四部电影的类别统计为爱情片:动作片=3:1，出现频率最 高的类别为爱情片，所以在k=4时，绿点电影的类别为爱情片。这个判别过程就是k-近邻算法。

二、k-近邻算法的Python实现

1. 算法实现

1.构建已经分类好的原始数据集

为了方便验证，这里使用python的字典dict构建数据集，然后再将其转化成DataFrame格式。

import pandas as pd
rowdata={‘电影名称‘:[‘无问西东‘,‘后来的我们‘,‘前任3‘,‘红海行动‘,‘唐人街探案‘,‘战狼2‘],
‘打斗镜头‘:[1,5,12,108,112,115],
‘接吻镜头‘:[101,89,97,5,9,8],
‘电影类型‘:[‘爱情片‘,‘爱情片‘,‘爱情片‘,‘动作片‘,‘动作片‘,‘动作片‘]}
movie_data= pd.DataFrame(rowdata)
movie_data

　　2.计算已知类别数据集中的点与当前点之间的距离

new_data = [24,67]
dist = list((((movie_data.iloc[:6,1:3]-new_data)**2).sum(1))**0.5)
dist

　　3.将距离升序排列，然后选取距离最小的k个点

dist_l = pd.DataFrame({‘dist‘: dist, ‘labels‘: (movie_data.iloc[:6, 3])})
dr = dist_l.sort_values(by = ‘dist‘)[: 4]
dr

　　4.确定前k个点所在类别的出现频率

re = dr.loc[:,‘labels‘].value_counts()
re

　　5.选择频率最高的类别作为当前点的预测类别

result = []
result.append(re.index[0])
result

2. 封装函数

import pandas as pd
"""
函数功能：KNN分类器
参数说明：
new_data:需要预测分类的数据集
dataSet:已知分类标签的数据集（训练集）
k:k-近邻算法参数，选择距离最小的k个点
返回：
result：分类结果
"""
def classify0(inX,dataSet,k):
　　result = []
　　dist = list((((dataSet.iloc[:,1:3]-inX)**2).sum(1))**0.5)
　　dist_l = pd.DataFrame({‘dist‘:dist,‘labels‘:(dataSet.iloc[:, 3])})
　　dr = dist_l.sort_values(by = ‘dist‘)[: k]
　　re = dr.loc[:, ‘labels‘].value_counts()
　　result.append(re.index[0])
　　return result

测试函数运行结果

inX = new_data
dataSet = movie_data
k = 3
classify0(inX,dataSet,k)

这就是我们使用k-近邻算法构建的一个分类器，根据我们的“经验”可以看出，分类器给的答案还是比较符合我们的 预期的。

学习到这里，有人可能会问：”分类器何种情况下会出错？“或者”分类器给出的答案是否永远都正确？“答案一定是 否定的，分类器并不会得到百分百正确的结果，我们可以使用很多种方法来验证分类器的准确率。此外，分类器的 性能也会受到很多因素的影响，比如k的取值就在很大程度上影响了分类器的预测结果，还有分类器的设置、原始 数据集等等。为了测试分类器的效果，我们可以把原始数据集分为两部分，一部分用来训练算法（称为训练集）， 一部分用来测试算法的准确率（称为测试集）。同时，我们不难发现，k-近邻算法没有进行数据的训练，直接使用 未知的数据与已知的数据进行比较，得到结果。因此，可以说，k-近邻算法不具有显式的学习过程。

三、k-近邻算法之约会网站配对效果判定

海伦一直使用在线约会网站寻找适合自己的约会对象，尽管约会网站会推荐不同的人选，但她并不是每一个都喜 欢，经过一番总结，她发现曾经交往的对象可以分为三类：

不喜欢的人

魅力一般的人

极具魅力得人

海伦收集约会数据已经有了一段时间，她把这些数据存放在文本文件datingTestSet.txt中，其中各字段分别为：

1. 每年飞行常客里程

2. 玩游戏视频所占时间比

3. 每周消费冰淇淋公升数

1. 准备数据

datingTest = pd.read_table(‘datingTestSet.txt‘,header=None)
datingTest.head()
datingTest.shape
datingTest.info()

2. 分析数据

使用 Matplotlib 创建散点图，查看各数据的分布情况

%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
#把不同标签用颜色区分
Colors = []
for i in range(datingTest.shape[0]):
　　m = datingTest.iloc[i,-1]
　　if m==‘didntLike‘:
　　　　Colors.append(‘black‘)
　　if m==‘smallDoses‘:
　　　　Colors.append(‘orange‘)
　　if m==‘largeDoses‘:
　　　　Colors.append(‘red‘)
#绘制两两特征之间的散点图
plt.rcParams[‘font.sans-serif‘]=[‘Simhei‘] #图中字体设置为黑体
pl=plt.figure(figsize=(12,8))
fig1=pl.add_subplot(221)
plt.scatter(datingTest.iloc[:,1],datingTest.iloc[:,2],marker=‘.‘,c=Colors)
plt.xlabel(‘玩游戏视频所占时间比‘)
plt.ylabel(‘每周消费冰淇淋公升数‘)

fig2=pl.add_subplot(222)
plt.scatter(datingTest.iloc[:,0],datingTest.iloc[:,1],marker=‘.‘,c=Colors)
plt.xlabel(‘每年飞行常客里程‘)
plt.ylabel(‘玩游戏视频所占时间比‘)

fig3=pl.add_subplot(223)
plt.scatter(datingTest.iloc[:,0],datingTest.iloc[:,2],marker=‘.‘,c=Colors)
plt.xlabel(‘每年飞行常客里程‘)
plt.ylabel(‘每周消费冰淇淋公升数‘)
plt.show()

3. 数据归一化

下表是提取的4条样本数据，如果我们想要计算样本1和样本2之间的距离，可以使用欧几里得计算公式：

 

 

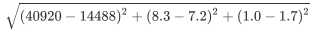
序号	每年飞行常客里程	玩游戏视频所占时间比	每周消费冰淇淋公升数	分类
1	40920	8.3	1.0	largeDoses
2	14488	7.2	1.7	smallDoses
3	26052	1.4	0.8	didntLike
4	75136	13.1	0.4	didntLike

表3 4条样本数据

我们很容易发现，上面公式中差值最大的属性对计算结果的影响最大，也就是说每年飞行常客里程对计算结果的影 响远远大于其他两个特征，原因仅仅是因为它的数值比较大，但是在海伦看来这三个特征是同等重要的，所以接下 来我们要进行数值归一化的处理，使得这三个特征的权重相等。

数据归一化的处理方法有很多种，比如0-1标准化、Z-score标准化、Sigmoid压缩法等等，在这里我们使用最简单 的0-1标准化，公式如下：

　　　　　　

 

"""
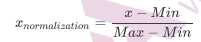
函数功能：归一化
参数说明：
dataSet:原始数据集
返回：0-1标准化之后的数据集
"""
def minmax(dataSet):
    minDf = dataSet.min()
    maxDf = dataSet.max()
    normSet = (dataSet - minDf )/(maxDf - minDf)
    return normSet

datingT = pd.concat([minmax(datingTest.iloc[:, :3]), datingTest.iloc[:,3]], axis=1)
datingT.head()

4. 划分训练集和测试集

 前面概述部分我们有提到，为了测试分类器的效果，我们可以把原始数据集分为训练集和测试集两部分，训练集用 来训练模型，测试集用来验证模型准确率。

关于训练集和测试集的切分函数，网上一搜一大堆，Scikit Learn官网上也有相应的函数比如model_selection 类中 的train_test_split 函数也可以完成训练集和测试集的切分。

通常来说，我们只提供已有数据的90%作为训练样本来训练模型，其余10%的数据用来测试模型。这里需要注意的 10%的测试数据一定要是随机选择出来的，由于海伦提供的数据并没有按照特定的目的来排序，所以我们这里可以 随意选择10%的数据而不影响其随机性。

"""
函数功能：切分训练集和测试集
参数说明：
dataSet:原始数据集
rate:训练集所占比例
返回：切分好的训练集和测试集
"""
def randSplit(dataSet,rate=0.9):
    n = dataSet.shape[0]
    m = int(n*rate)
    train = dataSet.iloc[:m,:]
    test = dataSet.iloc[m:,:]
    test.index = range(test.shape[0])
    return train,test


train,test = randSplit(datingT)
train
test

5. 分类器针对于约会网站的测试代码

接下来，我们一起来构建针对于这个约会网站数据的分类器，上面我们已经将原始数据集进行归一化处理然后也切 分了训练集和测试集，所以我们的函数的输入参数就可以是train、test和k(k-近邻算法的参数，也就是选择的距离 最小的k个点)。

"""
函数功能：k-近邻算法分类器
参数说明：
train:训练集
test：测试集
k:k-近邻参数，即选择距离最小的k个点
返回：预测好分类的测试集
"""
def datingClass(train,test,k):
　　n = train.shape[1] - 1
　　m = test.shape[0]
　　result = []
　　for i in range(m):
　　　　dist = list((((train.iloc[:, :n] - test.iloc[i, :n]) ** 2).sum(1))**5)
　　　　dist_l = pd.DataFrame({‘dist‘: dist, ‘labels‘: (train.iloc[:, n])})
　　　　dr = dist_l.sort_values(by = ‘dist‘)[: k]
　　　　re = dr.loc[:, ‘labels‘].value_counts()
　　　　result.append(re.index[0])
　　result = pd.Series(result)
　　test[‘predict‘] = result
　　acc = (test.iloc[:,-1]==test.iloc[:,-2]).mean()
　　print(f‘模型预测准确率为{acc}‘)
　　return test

最后，测试上述代码能否正常运行，使用上面生成的测试集和训练集来导入分类器函数之中，然后执行并查看分类 结果。

datingClass(train,test,5)

从结果可以看出，我们模型的准确率还不错，这是一个不错的结果了。

四、算法总结

算法功能：分类（核心），回归

算法类型：有监督学习 - 惰性学习，距离类模型

数据输入：包含数据标签y，且特征空间中至少包含k个训练样本（k>=1) 特征空间中各个特征的量纲需统一，若不统一则需要进行归一化处理 自定义的超参数k (k>=1)

模型输出：在KNN分类中，输出是标签中的某个类别，在KNN回归中，输出是对象的属性值，该值是距离输入的数据最近的k个训练样本标签的平均值

1. 优点

　　简单好用，容易理解，精度高，理论成熟，既可以用来做分类也可以用来做回归

　　可用于数值型数据和离散型数据

　　无数据输入假定

　　适合对稀有事件进行分类

2. 缺点

　　计算复杂性高；空间复杂性高；

　　计算量太大，所以一般数值很大的时候不用这个，但是单个样本又不能太少，否则容易发生误分。

　　样本不平衡问题（即有些类别的样本数量很多，而其它样本的数量很少）

　　可理解性比较差，无法给出数据的内在含义