Normalization

Posted 2020-12-16 super-zheng

机器学习领域有个很重要的假设：独立同分布假设，就是假设训练数据和测试数据是满足相同分布的，这是通过训练数据获得的模型能够在测试集获得好的效果的一个基本保障。神经网络学习过程本质上是为了学习数据的分布，一旦训练数据与测试数据的分布不同，那么网络的泛化能力也大大降低；另一方面，一旦在mini-batch梯度下降训练的时候，每批训练数据的分布不相同，那么网络就要在每次迭代的时候去学习以适应不同的分布，这样将会大大降低网络的训练速度，所以需要一种能够将数据分布搞到一致的方法。

更好的解决这个问题是用白化（whitening），白化（Whitening）是机器学习里面常用的一种规范化数据分布的方法，主要是PCA白化与ZCA白化，但是白化很复杂，所以就用简单的归一化normalization代替白化，我们只负责把数据均值和方差控制一致。

我们假设输入数据维度为N*H*W*C,N表示batchsize，H何W为高和宽，C为通道数。

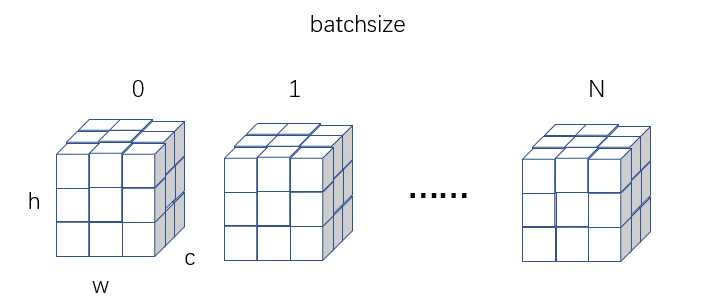
BN

BN（Batch Normalization）层的作用

（1）加速收敛（2）控制过拟合，可以少用或不用Dropout和正则（3）降低网络对初始化权重不敏感（4）允许使用较大的学习率

 

 

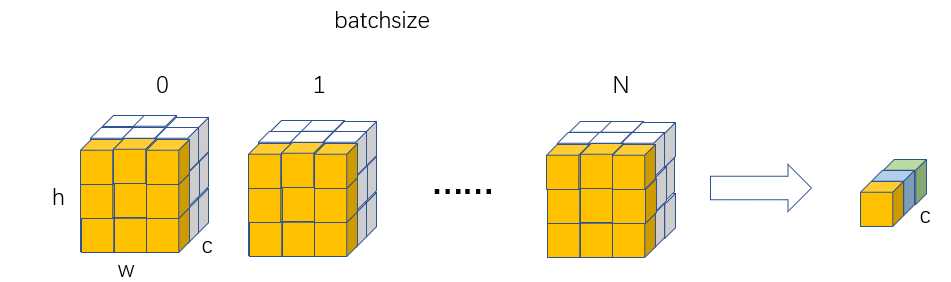
对于BN，其归一化维度是N、HxW维度，故其可学习权重维度是(C,)，其实就是BN的weight和bias维度，也就是论文中的 α和β。

 

 

 BN本质意思就是在Batch和HxW维度进行归一化，可以看出和batch相关，如果batch比较小，那么可能统计就不准确。并且由于测试时候batch可能和训练不同，导致分布不一致，故还多了两个参数：全局统计的均值和方差值，可以用从所有训练实例中获得的统计量来代替Batch里面m个训练实例获得的均值和方差统计量，因为本来就打算用全局的统计量，只是因为计算量等太大所以才会用Batch这种简化方式的，那么在推理的时候直接用全局统计量即可。每次做Batch训练时，都会有那个Mini-Batch里m个训练实例获得的均值和方差，现在要全局统计量，只要把每个Batch的均值和方差统计量记住，然后对这些均值和方差求其对应的数学期望即可得出全局统计量，在测试的时候使用该统计量就好。

 

LN

BN有两个明显不足：

1、高度依赖于mini-batch的大小，实际使用中会对mini-Batch大小进行约束，不适合类似在线学习（mini-batch为1）情况；

2、不适用于RNN网络中normalize操作：BN实际使用时需要计算并且保存某一层神经网络mini-batch的均值和方差等统计信息，对于对一个固定深度的前向神经网络（DNN，CNN）使用BN，很方便；但对于RNN来说，sequence的长度是不一致的，换句话说RNN的深度不是固定的，不同的time-step需要保存不同的statics特征，可能存在一个特殊sequence比其的sequence长很多，这样training时，计算很麻烦。

但LN可以有效解决上面这两个问题。

 

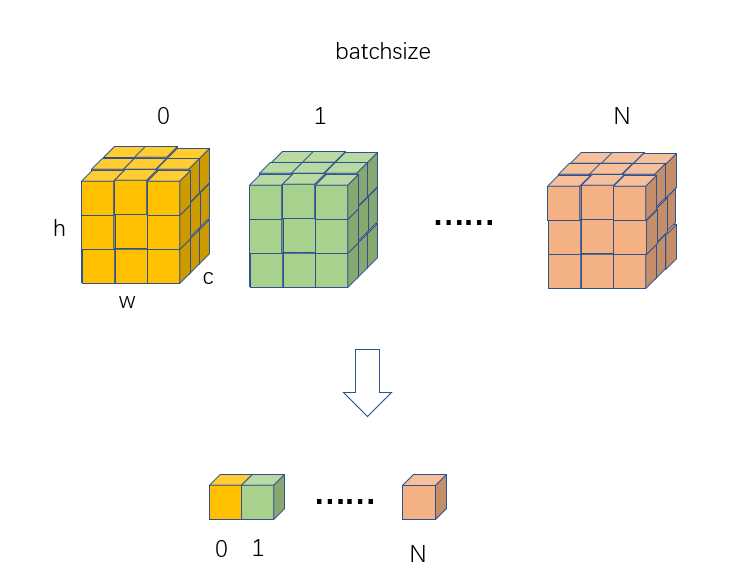
 对batch输入计算均值和方差(C、H和W维度求均值)，输出维度为(N,)，然后对输入(N,C,H,W)采用计算出来的(N,)个值进行广播归一化操作，最后再乘上可学习的(C,H,W)个权重参数即可。LN的归一化维度还可以在H*W*C上减少，比如H*W,那么每个样本得到C维向量，使用该向量对该样本归一化，反正就是不能用batch维度的信息，智能用样本自己进行归一化。这样训练和测试就可以一样。

 

IN

 

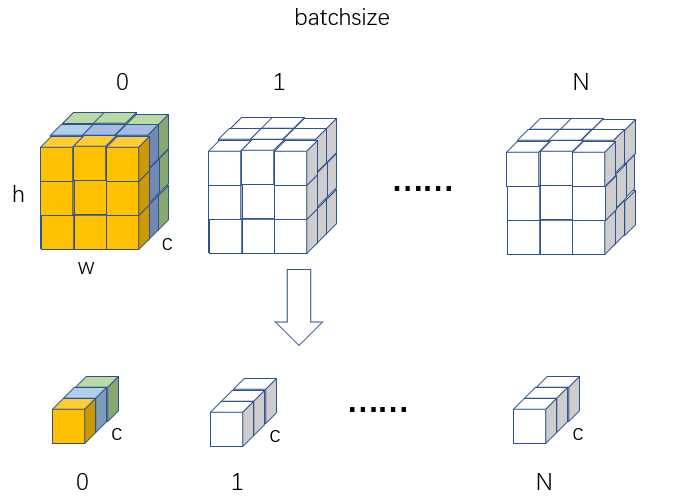
 其归一化维度最简单，就是HxW，对batch输入计算均值和方差(H,W维度求均值方差)，输出维度为(N,C),然后对输入(N,C,H,W)采用计算出来的(N,C)个值进行广播归一化操作，最后再乘上可学习的(C,)个权重参数即可。和BN的区别就是不使用batch信息。

 

GN

GN是介于LN和IN之间的操作，多了一个group操作。就是说一张图可以选择某些通道共用计算的值：

 

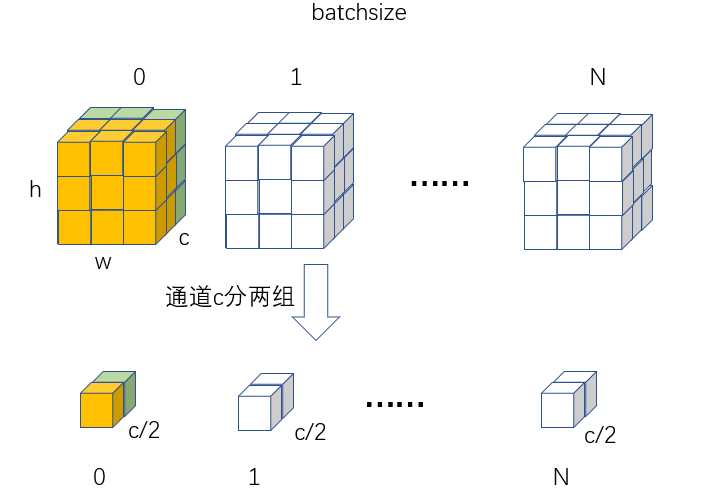
 对batch输入计算均值和方差(C/组数、H,W维度求均值方差)，输出维度为(N,组数),然后对输入(N,C,H,W)采用计算出来的(N,组数)个值进行广播归一化操作，最后再乘上可学习的(C,)个权重参数即可。

 

一定要注意归一化层是一个可学习的层，有缩放参数α和偏置β需要学习。