组合总和 I（力扣第39题）

Posted 2020-12-16 yxym2016

题目：

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：

所有数字（包括 target）都是正整数。
解集不能包含重复的组合。 

示例：

输入: candidates = [2,3,6,7], target = 7,
所求解集为:
[
  [7],
  [2,2,3]
]

分析：

　　给定的数组中的元素是不重复的，但是数组中的元素在同一条搜索路径中是可以无限制选取的，只要能够凑成target这个目标数。这也就意味着，当我们在搜索的时候，从当前的点往下进行搜索的时候，可以选择的范围是数组中所有的元素。下面我们通过一个具体的例子分析搜索结果的整个过程，数组[2,3,5]，target=8，其结果搜索过程如下图：

 

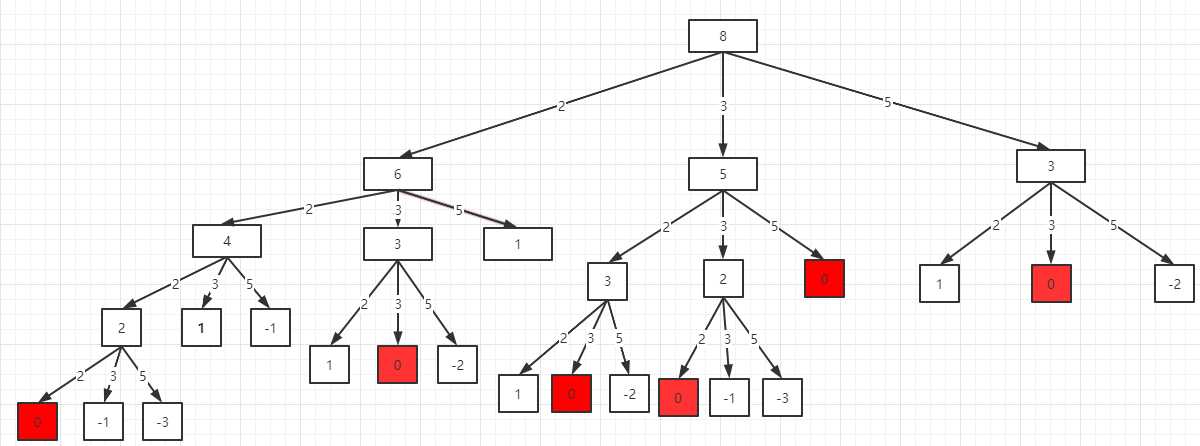
　　在上面的图中，从根节点到红色叶子结点的路径是能够凑成最终结果的路径，对应分支上的值就是组合成target的元素值，但是我们发现这些路径中的元素组合存在重复的情况，这是我们不想看到的，所以需要进行去重处理，那么应该怎么去重呢？先统计一下这些路径：

　　2-2-2-2

　　2-3-3

　　3-2-3

　　3-3-2

　　3-5

　　5-3

　我们发现第二组合和第三个组合是重复的，重复的原因在于这些元素在搜索路径中的顺序不一样，所以就产生了一条新的路径，也能凑成target，那么应该怎么办呢？很简单，就让搜索路径中，位于前面的分支的值要小于等于后面分支的值，这就能够将重复的组合去掉，从图中观察也正是这样的规律：重复的组合产生的原因就是，由于每次搜索的可选范围都是数组中的所有元素，所以就出现了前面分支中的元素值大于后面元素值的情况，这就可能会造成重复。我们可以以上一次搜索的元素值作为下一次搜索的遍历起始值，来达到这样的效果。同时要时刻判断当前搜索元素值是否大于target，如果大于直接跳过，节省时间。

代码实现：

 private List<List<Integer>> resList;

    public List<List<Integer>> combinationSum(int[] candidates, int target) {

        resList = new ArrayList<>();
        List<Integer> curRes = new ArrayList<>();
        
        findCombinationByDFS(candidates,target,curRes,0);
        return resList;
    }

    private void findCombinationByDFS(int[] candidates, int target, List<Integer> curRes,int start) {
        
        if (target == 0){
            resList.add(new ArrayList<>(curRes));
            return;
        }

        for (int i = start; i < candidates.length; i++) {
            
            if (candidates[i] <= target){
                
                curRes.add(candidates[i]);
                findCombinationByDFS(candidates,target-candidates[i],curRes,i);
                curRes.remove(curRes.size()-1);
            }
        }
        
    }