POJ-2318 TOYS(二分)(叉乘)(判断点在直线的哪侧)

Posted 2020-12-16 pixel-teee

题意:给出一个箱子的左上角和右下角的坐标，可以插入一些板子，每块板子的上顶点和下顶点。然后给定一堆玩具，扔到箱子里，求每个分隔区域里面的玩具数量。

分析:因为板子的坐标是按顺序从小到大给出的，我们的一个点，如果在一个板子的左边，那么就在这块板子后面的板子的坐标，但是在左侧板子的右边，具有单调性，可以用二分。判断一个点是否在一个直线的左右侧的时候，我们可以使用叉乘。

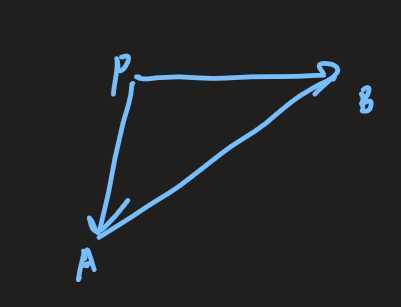
如果(vec{pa} imes vec{pb}) < 0，表示(p)点在(AB)的左侧，如果>0，表示在(AB)的右侧，== 0则表示在(AB)的线上。

(时间复杂度o(mlogn)，n表示板子的数量，m表示玩具，logn表示对n块板子的位置二分。)

#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <cmath>
#include <algorithm>

using namespace std;

const double eps = 1e-10;
const double PI = acos(-1.0);

struct Point
{
	double x, y;
	Point(double x = 0, double y = 0) :x(x), y(y) {}
	void operator=(const Point& rhs)
	{
		this->x = rhs.x;
		this->y = rhs.y;
	}
};

typedef Point Vector;

//向量 + 向量 = 向量， 点 + 向量 = 点
Vector operator + (Vector A, Vector B) { return Vector(A.x + B.x, A.y + B.y); }

//点 - 点 = 向量
Vector operator - (Point A, Point B) { return Vector(A.x - B.x, A.y - B.y); }

//向量 * 标量 = 向量
Vector operator * (Vector A, double p) { return Vector(A.x * p, A.y * p); }

//向量 / 数 = 向量
Vector operator / (Vector A, double p) { return Vector(A.x / p, A.y / p); }

int dcmp(double x)
{
	if (fabs(x) < eps) return 0;
	else return x < 0 ? -1 : 1;
}

bool operator<(const Point& a, const Point& b)
{
	return dcmp(a.x - b.x) < 0 || dcmp(a.x - b.x) == 0 && dcmp(a.y - b.y) < 0;
}

bool operator == (const Point& a, const Point& b)
{
	return dcmp(a.x - b.x) == 0 && dcmp(a.y - b.y) == 0;
}

//求叉积
double Cross(Vector A, Vector B) { return A.x * B.y - A.y * B.x; }
double Dot(Vector A, Vector B) { return A.x * B.x + A.y * B.y; }
double Length(Vector A) { return sqrt(Dot(A, A)); }

Vector Normal(Vector A)
{
	double L = Length(A);
	return Vector(-A.y / L, A.x / L);
}

struct Line {
	Point p;
	Vector v;
	Line() {};
	Line(Point p, Vector v) :p(p), v(v) { }
	//直线上的点坐标
	Point point(double t) {
		return p + v * t;
	}
	//平移直线d距离
	Line move(double d) {
		return Line(p + Normal(v) * d, v);
	}
};

const int N = 5050;
Line lines[N];

int cnt[N];

bool check(Point q, int mid)
{
	//直线两端的点
	Point a = lines[mid].point(1);
	Point b = lines[mid].point(0);

	Vector qa(a - q);
	Vector qb(b - q);

	if (dcmp(Cross(qa, qb)) < 0) return true;
	return false;
}

void init()
{
	memset(lines, 0, sizeof lines);
	memset(cnt, 0, sizeof cnt);
}

int main()
{
	int n, m;
	double x1, y1, x2, y2;

	while (scanf("%d", &n) != EOF)
	{
		if (n == 0) break;
		scanf("%d%lf%lf%lf%lf", &m, &x1, &y1, &x2, &y2);

		lines[0].p = Point(0, y2);
		lines[0].v = Point(x1, y1 - y2);
		//每个隔板的直线
		double t, b;
		for (int i = 1; i <= n; ++i)
		{
			scanf("%lf%lf", &t, &b);
			lines[i].p = Point(b, y2);
			lines[i].v = Point(t - b, y1 - y2);
		}

		lines[n + 1].p = Point(x2, y2);
		lines[n + 1].v = Point(0, y1 - y2);

		double toyx, toyy;
		//m个玩具
		for (int i = 1; i <= m; ++i)
		{
			scanf("%lf%lf", &toyx, &toyy);
			Point toy(toyx, toyy);
			//二分在哪个板子左侧
			int l = 0, r = n + 1;
			while (l < r)
			{
				int mid = l + r >> 1;
				if (check(toy, mid)) r = mid;
				else l = mid + 1;
			}
			++cnt[l - 1];
		}

		for (int i = 0; i <= n; ++i)
		{
			printf("%d: %d
", i, cnt[i]);
		}
		puts("");
		init();
	}
	return 0;
}