UVA-11437 Triangle Fun(梅涅劳斯定理)(三等分点)

Posted 2020-12-16 pixel-teee

题意:如下是一个三角形ABC.(点D,E和F是三角形ABC的三等分点,)求(三角形PQR)的面积。

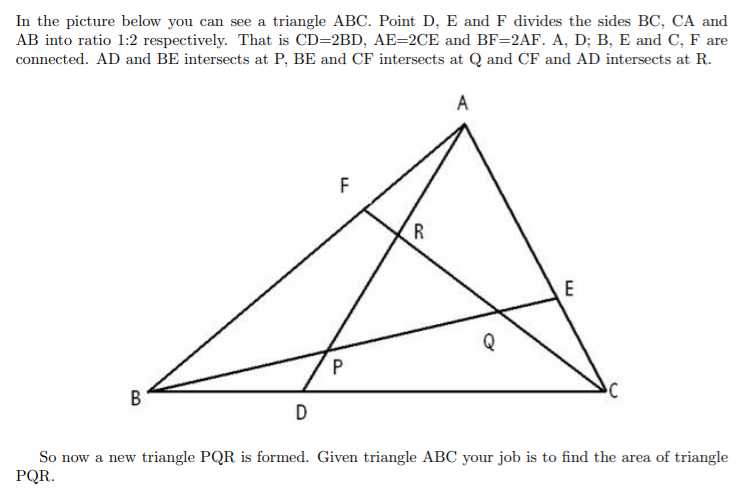
分析:三等分点的坐标可以推导出来，比如求D的坐标，D的坐标为((frac{2 * B.x + C.x}{3}, frac{2 * B.y + C.y}{3}))，然后求出(三个交点P, R, Q)，求出向量(vec{pr})和(vec{pq})的夹角，然后利用公式(frac{1}{2}*|pr|*|pq|*sinangle{RPQ})求出三角形面积。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <cmath>
#include <algorithm>

using namespace std;

const double eps = 1e-10;
const double PI = acos(-1.0);
struct Point
{
	double x, y;
	Point(double x = 0, double y = 0) : x(x), y(y) {}
};

typedef Point Vector;

//向量 + 向量 = 向量， 点 + 向量 = 点
Vector operator + (Vector A, Vector B) { return Vector(A.x + B.x, A.y + B.y); }

//点 - 点 = 向量
Vector operator - (Point A, Point B) { return Vector(A.x - B.x, A.y - B.y); }

//向量 * 标量 = 向量
Vector operator * (Vector A, double p) { return Vector(A.x * p, A.y * p); }

//向量 / 数 = 向量
Vector operator / (Vector A, double p) { return Vector(A.x / p, A.y / p); }

double Dot(Vector A, Vector B) { return A.x * B.x + A.y * B.y; }
double Cross(Vector A, Vector B) { return A.x * B.y - A.y * B.x; }
double Length(Vector A) { return sqrt(Dot(A, A)); }

Vector Normal(Vector A)
{
	double L = Length(A);
	return Vector(-A.y / L, A.x / L);
}

int dcmp(double x)
{
	if (fabs(x) < eps) return 0;
	else return x < 0 ? -1 : 1;
}

bool operator<(const Point& a, const Point& b)
{
	return dcmp(a.x - b.x) < 0 || dcmp(a.x - b.x) == 0 && dcmp(a.y - b.y) < 0;
}

bool operator == (const Point& a, const Point& b)
{
	return dcmp(a.x - b.x) == 0 && dcmp(a.y - b.y) == 0;
}

Point GetLineIntersection(Point P, Vector v, Point Q, Vector w)
{
	Vector u = P - Q;
	double t = Cross(w, u) / Cross(v, w);
	return P + v * t;
}

struct Line {
	Point p;
	Vector v;
	Line(Point p, Vector v) :p(p), v(v) { }
	//直线上的点坐标
	Point point(double t) {
		return p + v * t;
	}
	//平移直线d距离
	Line move(double d) {
		return Line(p + Normal(v) * d, v);
	}
};

Point GetLineIntersection(Line a, Line b)
{
	return GetLineIntersection(a.p, a.v, b.p, b.v);
}

double angle(Vector v)
{
	return atan2(v.y, v.x);
}

void out(Point a)
{
	cout << a.x << a.y << endl;
}

int main()
{
	//freopen("in.txt", "r", stdin);
	int t;
	scanf("%d", &t);
	for (int i = 1; i <= t; ++i)
	{
		double ax, ay, bx, by, cx, cy;
		scanf("%lf%lf%lf%lf%lf%lf", &ax, &ay, &bx, &by, &cx, &cy);
		Point A(ax, ay), B(bx, by), C(cx, cy);

		//f点(A, B的三等分点)
		Point F((2 * A.x + B.x) / 3, (2 * A.y + B.y) / 3);

		//d点(B, C的三等分点)
		Point D((2 * B.x + C.x) / 3, (2 * B.y + C.y) / 3);

		//e点(A, C的三等分点)
		Point E((2 * C.x + A.x) / 3, (2 * C.y + A.y) / 3);

		//直线ad
		Line ad(A, A - D);
		//直线be
		Line be(B, B - E);
		//直线cf
		Line cf(C, C - F);

		Point p = GetLineIntersection(ad, be);
		Point q = GetLineIntersection(be, cf);
		Point r = GetLineIntersection(ad, cf);

		Line pr(p, p - r);
		Line pq(p, p - q);

		double ang2 = angle(pq.v);
		double ang1 = angle(pr.v) - ang2;

		//pr和pq的夹角
		double ang = acos(Dot(pr.v, pq.v) / Length(pr.v) / Length(pq.v));

		//余弦定理
		double s = 1.0 / 2.0 * Length(pr.v) * Length(pq.v) * sin(ang);

		printf("%.0lf
", s);
	}

	return 0;
}