P4310 绝世好题 题解

Posted 2020-12-16 liuchanglc

题目描述

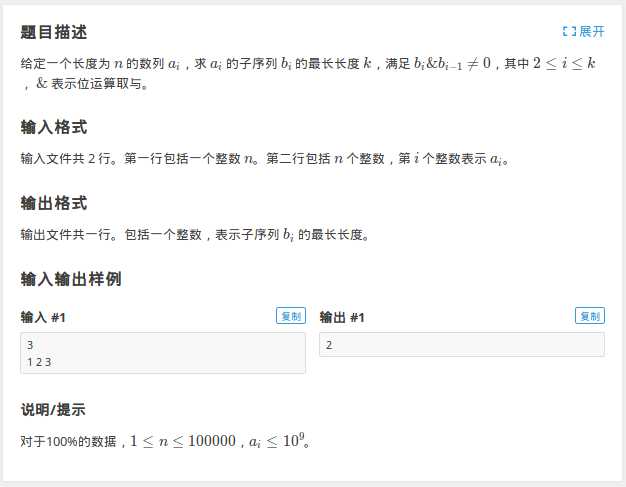
分析

第一次看这道题首先想到的就是时间复杂度为( n^{2})的求最长上升子序列

    for(int i=1;i<=n;i++){
        f[i]=1;
        for(int j=1;j<i;j++){
            if((a[i]&a[j])!=0) f[i]=max(f[i],f[j]+1);
        }
        ans=max(ans,f[i]);
    }

判断时把条件改一下就好了

但是这一道题的数据范围达到了(10^{5})，这样写会超时

所以我们考虑更优秀的算法，突破口就是位运算

题目中的操作是按位与，所以我们可以把一个数的每一个二进制位分别拆分进行计算

我们设(f[i])为当前二进制位为(i)时满足要求的最长长度

我们用一个变量(k)记录当前位置的最大状态

要注意的是，最大状态要在所有为(1)的位中转移

比如下面这组数据

011

110

100

在转移到第二位的时候要取一个最大值

最后不要忘了用这个值去更新(f)值

代码

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
int n,a[maxn],ans;
int f[300];
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;++i){
		scanf("%d",&a[i]);
	}
	for(int i=1;i<=n;++i){
	    int now=1;
		for(int j=0;j<=30;j++){
		    if(a[i]&(1<<j)){
		        now=max(now,f[j]+1);
		    } 
		}
		for(int j=0;j<=30;j++){
		    if(a[i]&(1<<j)){
		        f[j]=max(f[j],now);
		    }
		}
       ans=max(ans,now);
	}
	printf("%d
",ans);
	return 0;
}