7.8集训模拟赛（忘记板子）

Posted 2020-12-16 lightyachoo

A. 售票系统

题目描述

输入格式

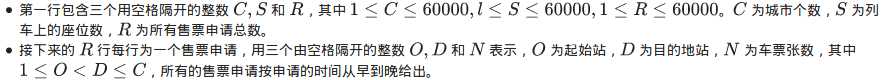
输出格式

 样例

样例输入

4 6 4
1 4 2
1 3 2
2 4 3
1 2 3

样例输出

YES
YES
NO
NO 

分析

 这道题就是一个线段树的区间修改和区间查询，但但但但是这道题n²可以过！！！！由于本人异常懒惰，就不写线段树的了，直接贴出暴力的代码，这个代码太危险，很容易TLE，还是找时间打打线段树的

Code

#include<bits/stdc++.h>
using namespace std;
const int N = 6e4+10;
int c,s,r;
int o,d,n;
int tree[N];

int main(){
    scanf("%d%d%d",&c,&s,&r);
    for(int i = 1;i <= r;i++){
        scanf("%d%d%d",&o,&d,&n);
        int maxn = -10;
        for(int j = o;j <= d-1;j++){
            maxn = max(maxn,tree[j]);
            if(s - maxn < n)break;
        }
        if(s - maxn >= n){
            printf("YES
");
            for(int j = o;j <= d-1;j++){
                tree[j] += n;
            }
        } else {
            printf("NO
");
        }
    }
    return 0;
}

B. 排队

题目描述

输入格式

输出格式

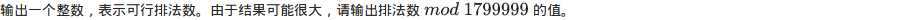
样例

样例输入

5 3

样例输出

15

数据范围与提示

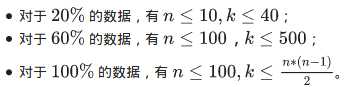
分析

小花，呵呵，我分班之前的英语老师就叫做“小花”。哎哎哎，远了远了。

很令我惊讶的是这道题竟然是递推，我还以为是什么归并排序，逆序对，树状数组呢。

1～n组成的序列中，如果是升序，那么逆序对就为0，如果是降序，那么逆序对就是1+2+3+4+...+n-1。

加入一个数，那么新产生的逆序对最多是i-1个。

所以我们定义f[i][j],表示1~i个数的i逆序对个数为j个时的方案数。

所以f[i][j] = f[i-1][j]+f[i-1][j-1]+f[i-1][j-1]+......+f[i-1][j-i+1].（1）

同理：f[i][j-1] = f[i-1][j-1]+f[i-1][j-2]+f[i-1][j-3]+......+f[i-1][j-i].（2）

由（1）-（2）得f[i][j] = f[i-1][j] + f[i][j-1] - f[i-1][j-1]。

Code

#include<bits/stdc++.h>
using namespace std;
const int N = 110;
const int mod = 1799999;
long long f[N][N*N];
int n,k;
int sum;

int main(){
    scanf("%d%d",&n,&k);
    for(int i = 1;i <= n;i++){
        f[i][0] = 1;
    }
    for(int i = 1;i <= n;i++){
        sum += (i-1);
        for(int j = 1;j <= k;j++){
            if(j > sum)break;
            f[i][j] = (f[i-1][j] + f[i][j-1])%mod;
            if(i <= j){//判断，不能是j-i小于零
                f[i][j] = (f[i][j] - f[i-1][j-i] + mod)%mod;//处处取模
            }
        }
    }
    printf("%lld
",f[n][k]%mod);
    return 0;
}

C. 优美值

题目描述

输入格式

输出格式

样例

样例输入

8
16 19 7 8 9 11 20 16
8
3 8
1 4
2 3
1 1
5 5
1 2
2 8
7 8

样例输出

7
3
1
3
5
3
7
3

数据范围与提示

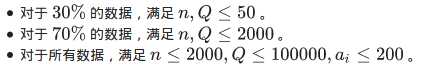
分析

 其实这道题我自己认为是比较玄学的，自己是真的理解了 ，但不知道该怎么非常的清楚的说出来，那就试着说吧。

如果第i个数a_i能成为中位数，那么它在它所在的区间比他大的一定和比他小的数量是一样的，所以我们就从a_i向左向右扫描，遇到比他大的sum++，比他小的sum--，然后以数量为坐标记录。

完事后如果左边比他打的有sum个，那么右边比他大的有-sum个，所以就就就找最大的......

Code

xiu

#include<bits/stdc++.h>
using namespace std;
const int N = 2e4+10;
int n;
int a[N];
int l[N],r[N],sum;
int maxn[N];
int Q;
int L,R;
void pre(){
    for(int i = 1;i <= n;i++){
        memset(l,-1,sizeof(l));
        memset(r,-1,sizeof(r));
        l[n] = 0,r[n] = 0;
        sum = 0;
        for(int j = i-1;j >= 1;j--){
            if(a[j] > a[i])sum++;
            if(a[j] <= a[i])sum--;
            l[sum+n] = i - j;
        }
        sum = 0;
        for(int j = i+1;j <= n;j++){
            if(a[j] >= a[i])sum++;
            if(a[j] < a[i])sum--;
            r[sum+n] = j - i;
        }
        for(int j = 1-i;j <= i-1;j++){
            if(l[j+n]>=0&&r[n-j]>=0)
                maxn[i] = max(maxn[i],l[j+n]+r[n-j]+1);
        }
    }
}

int main(){
    scanf("%d",&n);
    for(int i = 1;i <= n;i++)scanf("%d",&a[i]);
    pre();
    scanf("%d",&Q);
    for(int i = 1;i <= Q;i++){
        scanf("%d%d",&L,&R);
        int ans = -10;
        for(int j = L;j <= R;j++){
            ans = max(ans , maxn[j]);
        }
        printf("%d
",ans);
    }
    return 0;
}

 

D. 最短路径

题目描述

 

 

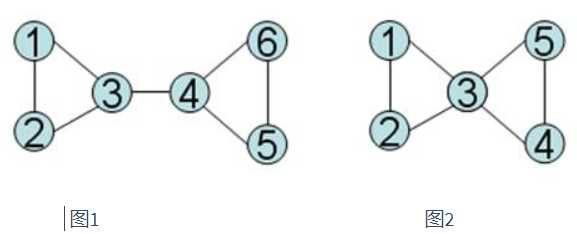
输入格式

输出格式

样例

样例输入

4 4
1 2 1
2 3 2
1 3 2
3 4 1
2
2 4
1 3

样例输出

3
2

数据范围与提示

分析

这这这是个烦人的玩意，这道题的来源是洛谷P5236,一大堆的题解，那就去看吧。我还不会呢。

Code

#include <bits/stdc++.h>
const int maxn=100005+100,maxm=300005;//因为有新增边，最大新增边为n，即一个大环
struct Node{
    int to,w,next;
}e[maxm];
int len=1,head[maxn],vis[maxn],dis[maxn],dep[maxn],f[maxn][14];
int n,m,Time,dfn[maxn];
int cnt,Circle[maxm],st[maxn],rd[maxn],belong[maxn],Girth[maxn];
void Insert(int x,int y,int z){//边的编号从2开始    
    e[++len].to=y;e[len].w=z;e[len].next=head[x];head[x]=len;
}
void spfa(int x) {
    memset(dis,0x3f,sizeof dis);
    std::queue<int> q; q.push(x);dis[x]=0;
    while(!q.empty()) {
        int u=q.front(); q.pop();vis[u]=0;
        for(int i=head[u];i;i=e[i].next){
            int v=e[i].to;
            if(dis[v]>dis[u]+e[i].w){
                dis[v]=dis[u]+e[i].w;
                if(!vis[v])
                    vis[v]=1,q.push(v);
            }
        }
    }
}
void Circ(int x,int y) {//y是环上最早访问的节点
    if(x==y) return;
    belong[x]=cnt;//记录节点x属于哪个环
    Insert(y,x,0);//只需要建y到x的边即可，因为lca时y时x的父亲节点
    Circle[st[x]]=Circle[st[x]^1]=1;//环上的边左上标记
    Girth[cnt]+=e[st[x]].w;//记录环的长度
    Circ(e[st[x]^1].to,y); 
}
void dfs(int x) {
    dfn[x]=++Time;
    for(int i=head[x];i;i=e[i].next){
        int v=e[i].to;
        if(i!=(st[x]^1)&&i<=m*2+1){//编号大于2*m+1的边是新建的环上的边
            if(!dfn[v]){
                rd[v]=rd[x]+e[i].w;//按搜索顺序记录v到根节点1的距离
                st[v]=i;//记录以v结尾的树枝边的编号
                dfs(v);
            } 
            else if(dfn[v]<dfn[x]){//出现简单环
                Girth[++cnt]=e[i].w;//cnt记录环的编号
                Circ(x,v);//处理环,v是环上最早访问的点
            } 
        }
    }
}
void dfs2(int u) {
    for(int i=1;(1<<i)<=dep[u];++i)
        f[u][i]=f[f[u][i-1]][i-1];
    for(int i=head[u];i;i=e[i].next){
        int v=e[i].to;
        if(!Circle[i] && !dep[v]){//边i不在环上v未访问
            f[v][0]=u;//倍增初始化
            dep[v]=dep[u]+1;
            dfs2(v);
        }
    }
}
int Query(int u,int v) {
    if(dep[u]<dep[v])std::swap(u,v);
    int a=u,b=v,len=dep[u]-dep[v],k=0;
    while(len){
        if(len & 1) u=f[u][k];
        ++k;len>>=1;
    }
    if(u==v)return dis[a]-dis[b];
    for(int i=13;i>=0;i--)
        if(f[u][i]!=f[v][i]){
            u=f[u][i];v=f[v][i];
        }
    if(belong[u] && belong[u]==belong[v]) {
        int r=abs(rd[u]-rd[v]);//u和v按搜索顺序在环的距离
        return dis[a]-dis[u]+dis[b]-dis[v]+std::min(r,Girth[belong[u]]-r);
    }
    return dis[a]+dis[b]-2*dis[f[u][0]];
}

int main() {
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++){
        int x,y,z;scanf("%d%d%d",&x,&y,&z);
        Insert(x,y,z);Insert(y,x,z);
    }
    spfa(1),dfs(1),dep[1]=1,dfs2(1);
    int q;scanf("%d",&q);
    while(q--){
        int x,y;scanf("%d%d",&x,&y);
        printf("%d
",Query(x,y));
    }
    return 0;
}