Tree

Posted 2020-12-16 spnooyseed

https://ac.nowcoder.com/acm/contest/6226/C
、

修修去年种下了一棵树，现在它已经有n个结点了。
修修非常擅长数数，他很快就数出了包含每个点的连通点集的数量。
澜澜也想知道答案，但他不会数数，于是他把问题交给了你。

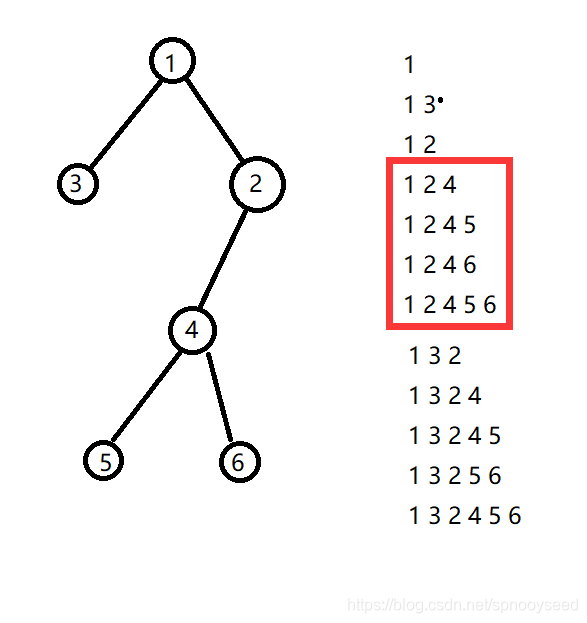
换根dp

1. 第一遍dfs ， 从下到上算贡献 ：对于样例中点1的情况，可以发现上述红色框里的，如果在4的子树里， 5 和 6两个点可选可不选 ， 一共2 * 2 中情况 ， 如果以dp[u] 表示u节点被选中的时候，其字数内选中情况为 dp[u] *= (dp[x] + 1) , dp[x] 时u的节点x选中的情况， +1是不选的情况，。
2. 第二遍dfs ， 从上到下算贡献 ： 当前根节点应该传给下一个孩子节点x的应该是 ：当前节点除去x节点贡献之后的dp[u] ， 即dp[u] / (dp[x] + 1) ， 可用逆元 , 但是恶心的地方出来了 ，万一(dp[x] + 1) % mod == 0的时候，算出来逆元也是0，传给孩子节点的值也是0，这样就糟糕了。所以特判一下
3. 如果不是特殊情况的话， u节点传给x节点的值就是ans[u] * qmi(dp[x] + 1 , mod - 2) , 用逆元除掉dp[x] + 1
4. 但是怎么特判呢，比赛的时候没想出来。赛后看别人代码也没看懂。后来慢慢想，看着代码想
   
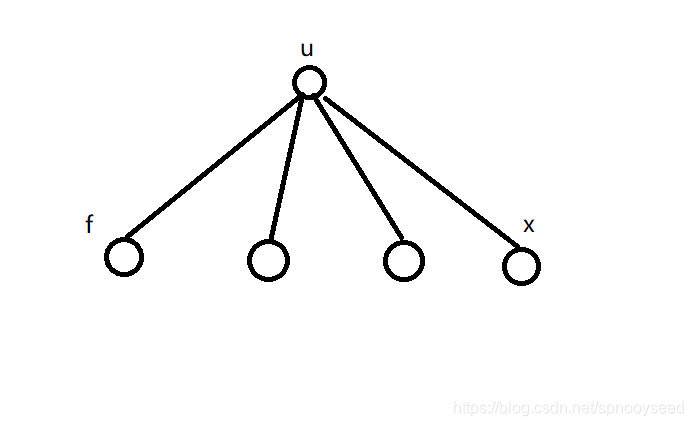
   5.上面这个图片情况下， 从f换根到u ， 现在从u换根到x的时候， 并且(dp[x] + 1) % mod == 0 , 也就是需要特判的情况，发现如果重新算一下 根据下面的代码

      res = 1 ;
      for(auto t : v[u]) {
        if(t == x ) continue ;
        res = res * (dp[t] + 1) % mod ;
      }

发现dp[f] 这个还包含了dp[u] ,因为第一次dfs的时候，dp[u]只包含子孩子节点的贡献， 现在f节点的孩子节点u变成了根节点，如果算u节点的时候还用dp[u] *= dp[f] + 1， 那这肯定错误 ， 所以就开一个数组sta[u]存一下当前节点从父亲节点那里传出来的值，这样肯定不会错误，因为在树中每个节点只有一个父亲节点，传出来的时候也只会一对一的传。那么算dp[u]不包含x节点贡献的时候，对于u的父亲节点f的贡献就是sta[u] + 1

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <unordered_map>
#include <vector>
#include <map>
#include <list>
#include <queue>
#include <cstring>
#include <cstdlib>
#include <ctime>
#include <cmath>
#include <stack>
#include <set>
#pragma GCC optimize(3 , "Ofast" , "inline")
using namespace std ;
#define ios ios::sync_with_stdio(false) , cin.tie(0) , cout.tie(0)
#define x first
#define y second
typedef long long ll ;
const double esp = 1e-6 , pi = acos(-1) ;
typedef pair<int , int> PII ;
const int N = 1e6 + 10 , INF = 0x3f3f3f3f , mod = 1e9 + 7;
ll in()
{
  ll x = 0 , f = 1 ;
  char ch = getchar() ;
  while(!isdigit(ch)) {if(ch == ‘-‘) f = -1 ; ch = getchar() ;}
  while(isdigit(ch)) x = x * 10 + ch - 48 , ch = getchar() ;
  return x * f ;
}
ll qmi(ll a, ll b)
{
  ll res = 1 ;
  while(b)
   {
     if(b & 1) res = res * a % mod ;
     a = a * a % mod ;
     b >>= 1 ;
   }
   return res ;
}
vector<int> v[N] ;
ll dp[N] , n ;
void dfs(int u , int f)
{
  dp[u] = 1 ;
  for(auto x : v[u]) {
    if(x == f) continue ;
    dfs(x , u) ;
    dp[u] = (dp[u] * (dp[x] + 1) % mod) % mod ;
  }
  return ;
}
ll ans[N] , sta[N] ;
void dfs1(int u , int f , ll sum)
{
  sum %= mod ;
  ans[u] = 1ll * dp[u] * sum % mod ;
  for(auto x : v[u]) {
    if(x == f) continue ;
    ll res = 1 ;
    if((dp[x] + 1) % mod) {
      res = (ans[u] * qmi(dp[x] + 1 , mod - 2) % mod) % mod  ;
    }
    else {
      res = sta[u] + 1 ;
      for(auto t : v[u]) {
        if(t == x || t == f) continue ;
        res = res * (dp[t] + 1) % mod ;
      }
   }
    sta[x] = res ;
    dfs1(x , u , res + 1) ;
  }
  return ;
}
int main()
{
  n = in() ;
  for(int i = 1; i < n ;i ++ )
   {
     int a = in() , b = in() ;
     v[a].push_back(b) , v[b].push_back(a) ;
   }
  dfs(1 , 0) ;
  dfs1(1 , 0 , 1) ;
  for(int i = 1; i <= n ;i ++ ) cout << ans[i] << endl ;
  return 0 ;
}
/*
*/