数据结构之二叉树

Posted 2020-12-16 tammy-yaoyao

数据结构之二叉树

一、认识数据结构

什么是数据结构？下面是维基百科的解释：

 

数据结构是计算机存储、组织数据的方式。数据结构意味着接口或封装：一个数据结构可被视为两个函数之间的接口，或者是由数据类型联合组成的存储内容的访问方法封装。

 

 

二、数据结构分类

常见的数据结构：

1、数组（Array）

2、栈（Stack）

3、队列（Queue）

4、链表（Linked List）

5、树（Tree）

6、图（Graph）

7、堆（Heap）

8、散列表（Hash）

 

 

三、树结构

树被描述为一种分层数据抽象模型，常用来描述数据间的层级关系和组织结构。树也是一种非顺序的数据结构。

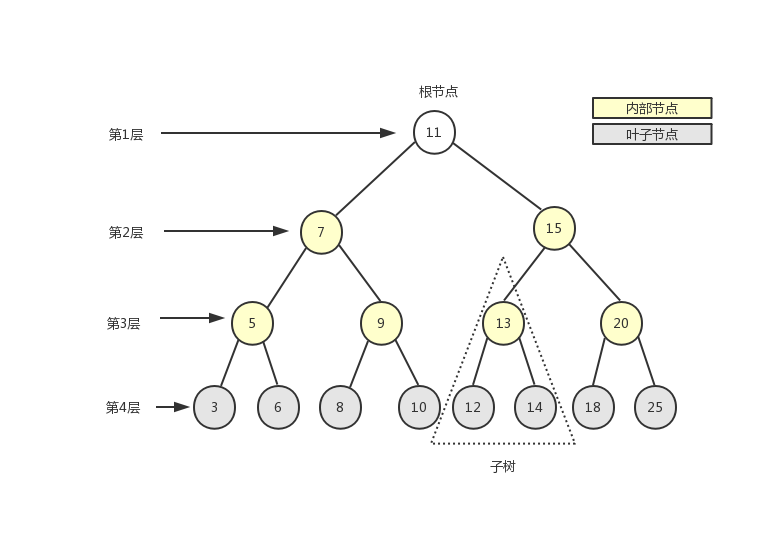
我们先介绍一些和树相关的术语。

　　如上图所示，一棵完整的树包含一个位于树顶部的节点，称之为根节点（11），它没有父节点。树中的每一个元素都叫做一个节点，节点分为内部节点（图中显示为黄色的节点）和外部节点（图中显示为灰色的节点），至少有一个子节点的节点称为内部节点，没有子元素的节点称为外部节点或叶子节点。一个节点可以有祖先（根节点除外）和后代。子树由节点本身和它的后代组成，如上图中三角虚框中的部分就是一棵子树。节点拥有的子树的个数称之为节点的度，如上图中除叶子节点的度为0外，其余节点的度都为2。从根节点开始，根为第1层，第一级子节点为第2层，第二级子节点为第3层，以此类推。树的高度（深度）由树中节点的最大层级决定（上图中树的高度为4）。

　　在一棵树中，具有相同父节点的一组节点称为兄弟节点，如上图中的3和6、5和9等都是兄弟节点。

 

 

四、二叉树

二叉树特点是每个结点最多只能有两棵子树，且有左右之分。左右子节点的顺序不能颠倒。因此，二叉树中不存在度大于2的节点。

 

 

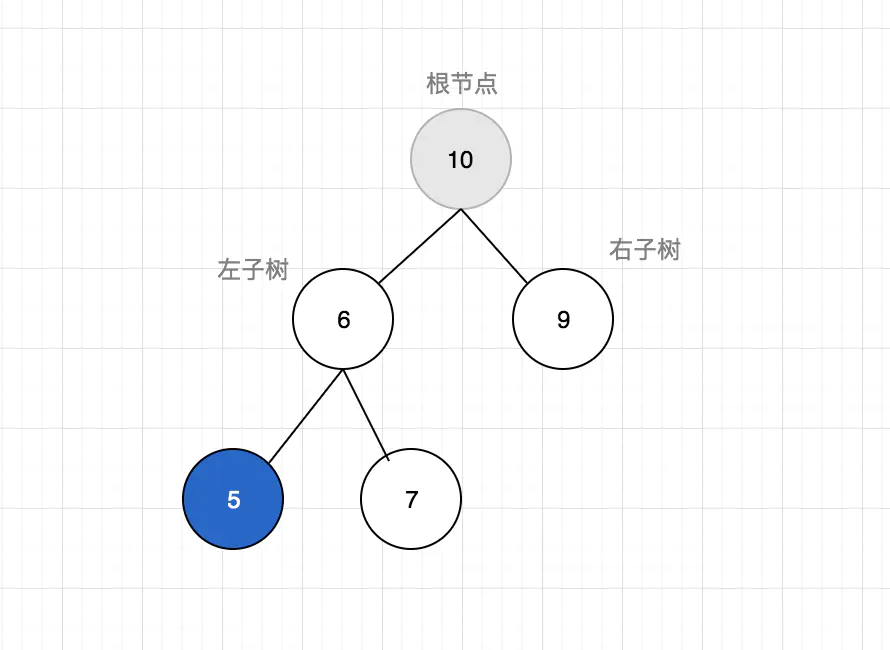
五、二叉搜索树（BST）

二叉搜索树（BST——Binary Search Tree）是二叉树的一种，它规定在左子节点上存储小（比父节点）的值，在右子节点上（比父节点）存储大（或等于）的值。下图就是一个二叉搜索树。

 

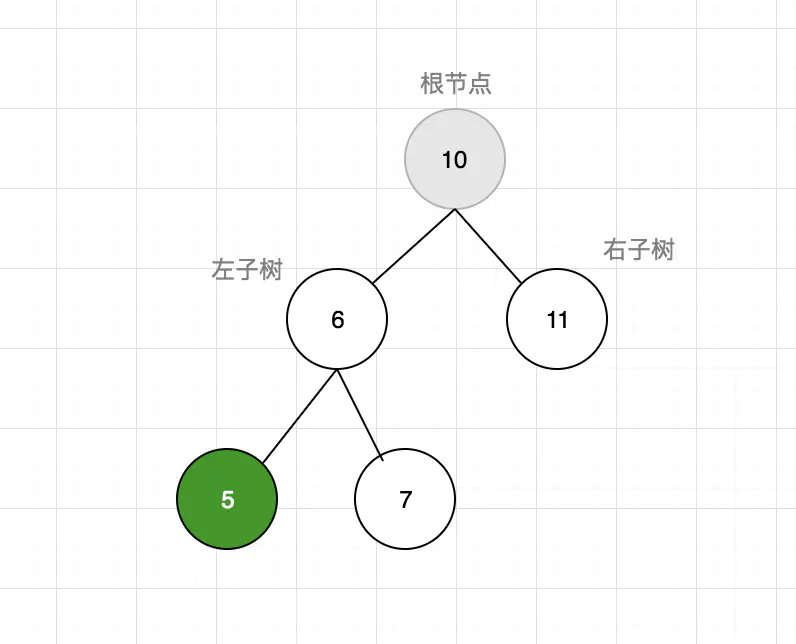
1，实现一个二叉搜索树

    class BinarySearchTree {
      constructor () {
          this.root = null;
          
      }
    
      // 向树中插入一个节点
      insert (key) {
        let Node = function(key) {
            this.key = key;
            this.left = null;
            this.right = null;
        }
        

        let insertNode = function (node, newNode) {
          if (newNode.key < node.key) {
              if (node.left === null) {
                    node.left = newNode;
              } else {
                  insertNode(node.left, newNode);
              }
          }
          else {
              if (node.right === null) {
                  node.right = newNode;
              } else {
                  insertNode(node.right, newNode);
              }
          }
        };
        let newNode = new Node(key);

        if (this.root === null) {
            this.root = newNode;
        } else {
            insertNode(this.root, newNode);
        }
      }
        
      getTree () {return this.root}
    }

    let tree = new BinarySearchTree()
    tree.insert(19)
    tree.insert(10)
    tree.insert(20)
    console.log(tree.getTree())

2，树遍历

树的三种遍历方式

• 前序遍历（NLR——Preorder Traversal）也叫先序遍历，先序遍历是以优先于后代节点的顺序访问每一个节点，访问根节点的操作发生在遍历其左右子树之前。
• 中序遍历（LNR——Inorder Traversal），中序遍历是一种以从最小到最大的顺序访问所有节点的遍历方式，访问根节点的操作发生在遍历其左右子树之间。
• 后序遍历（LRN——Postorder Traversal），后序遍历是先访问节点的后代节点，再访问节点本身，访问根节点的操作发生在遍历其左右子树之后。

 

前序遍历

this.preOrderTraverseNode = (node, callback) => {
  if (node !== null) {
    callback(node)
    this.preOrderTraverseNode(node.left, callback)
    this.preOrderTraverseNode(node.right, callback)
  }
 }

中序遍历

this.inOrderTraverseNode = (node, callback) => {
  if (node !== null) {
    this.inOrderTraverseNode(node.left, callback)
    callback(node)
    this.inOrderTraverseNode(node.right, callback)
  }
 }

后序遍历

this.postOrderTraverseNode = (node, callback) => {
  if (node !== null) {
    this.postOrderTraverseNode(node.left, callback)
    this.postOrderTraverseNode(node.right, callback)
    callback(node)
  }
}

3，树的搜索

搜索对象，一般是，特定的值，最大值，最小值

搜索特定的值

this.searchNode = (node, key) => {
  if (node === null) return false;
  if (node.key > key) {
    return this.searchNode(node.left, key)
  } else if (node.key < key) {
    return this.searchNode(node.right, key)
  } else {
    return true
  }
}

 

搜索最大值

max (){
  let node = this.root
  if (node === null) return null;
  while (node && node.right !== null) {
    node = node.right
  }
  return node
}

 

搜索最小值

min (Node) {
  let node = Node || this.root
  if (node === null) return null;
  while (node && node.left !== null) {
    node = node.left
  }
  return node
}

 

删除节点

this.removeNode = (node, key) => {
  if (node === null) return null;
  if (key < node.key) {
    node.left = this.removeNode(node.left, key)
    return node
  } else if (key > node.key) {
    node.right = this.removeNode(node.right, key)
    return node
  } else {
    //                     叶子节点
    if (node.left === null && node.right ) {
      node = null
      return node
    }
    if (node.left === null) {
      node = node.right
      return node
    } else if (node.right === null) {
      node = node.left
      return node
    }

    // 有两个子节点的节点情况
    let aux = this.min(node.right);
    node.key = aux.key;
    node.right = this.removeNode(node.right, aux.key);
    return node
  }

}

 

 

五、二叉树的应用

二叉树一般可以用来：

• 生成树结构
• 数据库的搜索算法
• 利用二叉树加密
• 计算目录和子目录中所有文件的大小，
• 打印一个结构化的文档
• 在游戏中用来做路径规划等