网格类问题的DFS遍历方法

Posted 2020-12-16 sbb-first-blog

网格问题的基本概念

我们首先明确一下岛屿问题中的网格结构是如何定义的，以方便我们后面的讨论。

网格问题是由 m*n个小方格组成一个网格，每个小方格与其上下左右四个方格认为是相邻的，要在这样的网格上进行某种搜索。

岛屿问题是一类典型的网格问题。每个格子中的数字可能是 0 或者 1。我们把数字为 0 的格子看成海洋格子，数字为 1 的格子看成陆地格子，这样相邻的陆地格子就连接成一个岛屿。

 

 

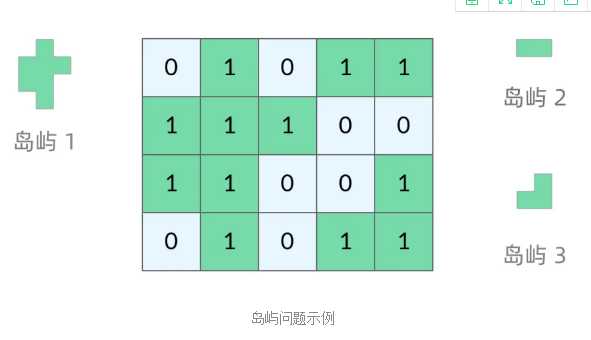
 在这样一个设定下，就出现了各种岛屿问题的变种，包括岛屿的数量、面积、周长等。不过这些问题，基本都可以用 DFS 遍历来解决。

DFS 的基本结构

网格结构要比二叉树结构稍微复杂一些，它其实是一种简化版的图结构。要写好网格上的 DFS 遍历，我们首先要理解二叉树上的 DFS 遍历方法，再类比写出网格结构上的 DFS 遍历。我们写的二叉树 DFS 遍历一般是这样的：

1 void traverse(TreeNode root) {
2     // 判断 base case
3     if (root == null) {
4         return;
5     }
6     // 访问两个相邻结点：左子结点、右子结点
7     traverse(root.left);
8     traverse(root.right);
9 }

可以看到，二叉树的 DFS 有两个要素：「访问相邻结点」和「判断 base case」。

要素一：访问相邻结点。二叉树的相邻结点非常简单，只有左子结点和右子结点两个。二叉树本身就是一个递归定义的结构：一棵二叉树，它的左子树和右子树也是一棵二叉树。那么我们的 DFS 遍历只需要递归调用左子树和右子树即可。

要素二：判断 base case。一般来说，二叉树遍历的 base case 是 root == null。这样一个条件判断其实有两个含义：一方面，这表示 root 指向的子树为空，不需要再往下遍历了。另一方面，在 root == null 的时候及时返回，可以让后面的 root.left 和 root.right 操作不会出现空指针异常。

 

对于网格上的 DFS，我们完全可以参考二叉树的 DFS，写出网格 DFS 的两个要素：

首先，网格结构中的格子有多少相邻结点？答案是上下左右四个。对于格子 (r, c) 来说（r 和 c 分别代表行坐标和列坐标），四个相邻的格子分别是 (r-1, c)、(r+1, c)、(r, c-1)、(r, c+1)。换句话说，网格结构是「四叉」的。

 

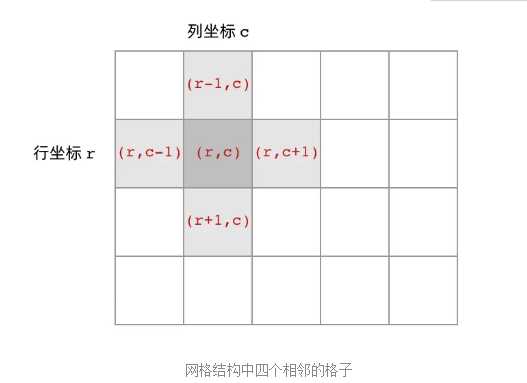
其次，网格 DFS 中的 base case 是什么？从二叉树的 base case 对应过来，应该是网格中不需要继续遍历、grid[r][c] 会出现数组下标越界异常的格子，也就是那些超出网格范围的格子。

 

 

 

 

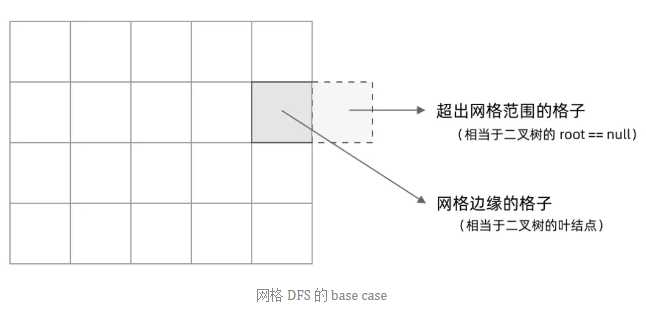
这一点稍微有些反直觉，坐标竟然可以临时超出网格的范围？这种方法我称为「先污染后治理」—— 甭管当前是在哪个格子，先往四个方向走一步再说，如果发现走出了网格范围再赶紧返回。这跟二叉树的遍历方法是一样的，先递归调用，发现 root == null 再返回。

这样，我们得到了网格 DFS 遍历的框架代码：

 1 void dfs(int[][] grid, int r, int c) {
 2     // 判断 base case
 3     // 如果坐标 (r, c) 超出了网格范围，直接返回
 4     if (!inArea(grid, r, c)) {
 5         return;
 6     }
 7     // 访问上、下、左、右四个相邻结点
 8     dfs(grid, r - 1, c);
 9     dfs(grid, r + 1, c);
10     dfs(grid, r, c - 1);
11     dfs(grid, r, c + 1);
12 }
13 
14 // 判断坐标 (r, c) 是否在网格中
15 boolean inArea(int[][] grid, int r, int c) {
16     return 0 <= r && r < grid.length 
17          && 0 <= c && c < grid[0].length;
18 }

如何避免重复遍历

网格结构的 DFS 与二叉树的 DFS 最大的不同之处在于，遍历中可能遇到遍历过的结点。这是因为，网格结构本质上是一个「图」，我们可以把每个格子看成图中的结点，每个结点有向上下左右的四条边。在图中遍历时，自然可能遇到重复遍历结点。

这时候，DFS 可能会不停地「兜圈子」，永远停不下来，如下图所示：

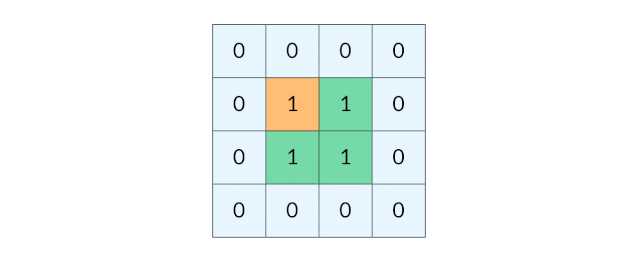
如何避免这样的重复遍历呢？答案是标记已经遍历过的格子。以岛屿问题为例，我们需要在所有值为 1 的陆地格子上做 DFS 遍历。每走过一个陆地格子，就把格子的值改为 2，这样当我们遇到 2 的时候，就知道这是遍历过的格子了。也就是说，每个格子可能取三个值：

• 0 —— 海洋格子
• 1 —— 陆地格子（未遍历过）
• 2 —— 陆地格子（已遍历过）

我们在框架代码中加入避免重复遍历的语句：

 1 void dfs(int[][] grid, int r, int c) {
 2     // 判断 base case
 3     if (!inArea(grid, r, c)) {
 4         return;
 5     }
 6     // 如果这个格子不是岛屿，直接返回
 7     if (grid[r][c] != 1) {
 8         return;
 9     }
10     grid[r][c] = 2; // 将格子标记为「已遍历过」
11     
12     // 访问上、下、左、右四个相邻结点
13     dfs(grid, r - 1, c);
14     dfs(grid, r + 1, c);
15     dfs(grid, r, c - 1);
16     dfs(grid, r, c + 1);
17 }
18 
19 // 判断坐标 (r, c) 是否在网格中
20 boolean inArea(int[][] grid, int r, int c) {
21     return 0 <= r && r < grid.length 
22          && 0 <= c && c < grid[0].length;
23 }

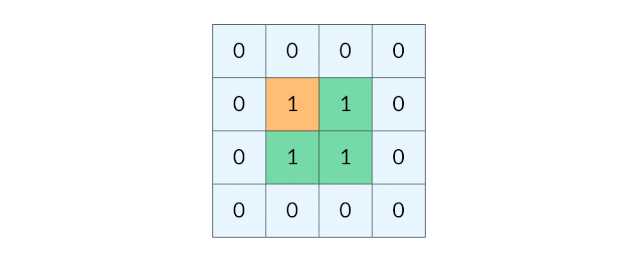
这样，我们就得到了一个岛屿问题、乃至各种网格问题的通用 DFS 遍历方法。以下所讲的几个例题，其实都只需要在 DFS 遍历框架上稍加修改而已。

 

 

 

 

1 int area(int[][] grid, int r, int c) {  
2     return 1 
3         + area(grid, r - 1, c)
4         + area(grid, r + 1, c)
5         + area(grid, r, c - 1)
6         + area(grid, r, c + 1);
7 }

最终我们得到的完整题解代码如下：

 1 public int maxAreaOfIsland(int[][] grid) {
 2     int res = 0;
 3     for (int r = 0; r < grid.length; r++) {
 4         for (int c = 0; c < grid[0].length; c++) {
 5             if (grid[r][c] == 1) {
 6                 int a = area(grid, r, c);
 7                 res = Math.max(res, a);
 8             }
 9         }
10     }
11     return res;
12 }
13 
14 int area(int[][] grid, int r, int c) {
15     if (!inArea(grid, r, c)) {
16         return 0;
17     }
18     if (grid[r][c] != 1) {
19         return 0;
20     }
21     grid[r][c] = 2;
22     
23     return 1 
24         + area(grid, r - 1, c)
25         + area(grid, r + 1, c)
26         + area(grid, r, c - 1)
27         + area(grid, r, c + 1);
28 }
29 
30 boolean inArea(int[][] grid, int r, int c) {
31     return 0 <= r && r < grid.length 
32          && 0 <= c && c < grid[0].length;
33 }

例题 2：岛屿的周长

LeetCode 463. Island Perimeter （Easy）

给定一个包含 0 和 1 的二维网格地图，其中 1 表示陆地，0 表示海洋。网格中的格子水平和垂直方向相连（对角线方向不相连）。整个网格被水完全包围，但其中恰好有一个岛屿（一个或多个表示陆地的格子相连组成岛屿）。

岛屿中没有“湖”（“湖” 指水域在岛屿内部且不和岛屿周围的水相连）。格子是边长为 1 的正方形。计算这个岛屿的周长。

 

 实话说，这道题用 DFS 来解并不是最优的方法。对于岛屿，直接用数学的方法求周长会更容易。不过这道题是一个很好的理解 DFS 遍历过程的例题，

我们再回顾一下 网格 DFS 遍历的基本框架：

 1 void dfs(int[][] grid, int r, int c) {
 2     // 判断 base case
 3     if (!inArea(grid, r, c)) {
 4         return;
 5     }
 6     // 如果这个格子不是岛屿，直接返回
 7     if (grid[r][c] != 1) {
 8         return;
 9     }
10     grid[r][c] = 2; // 将格子标记为「已遍历过」
11     
12     // 访问上、下、左、右四个相邻结点
13     dfs(grid, r - 1, c);
14     dfs(grid, r + 1, c);
15     dfs(grid, r, c - 1);
16     dfs(grid, r, c + 1);
17 }
18 
19 // 判断坐标 (r, c) 是否在网格中
20 boolean inArea(int[][] grid, int r, int c) {
21     return 0 <= r && r < grid.length 
22          && 0 <= c && c < grid[0].length;
23 }

可以看到，dfs 函数直接返回有这几种情况：

• !inArea(grid, r, c)，即坐标 (r, c) 超出了网格的范围，也就是我所说的「先污染后治理」的情况
• grid[r][c] != 1，即当前格子不是岛屿格子，这又分为两种情况：
• grid[r][c] == 0，当前格子是海洋格子
• grid[r][c] == 2，当前格子是已遍历的陆地格子

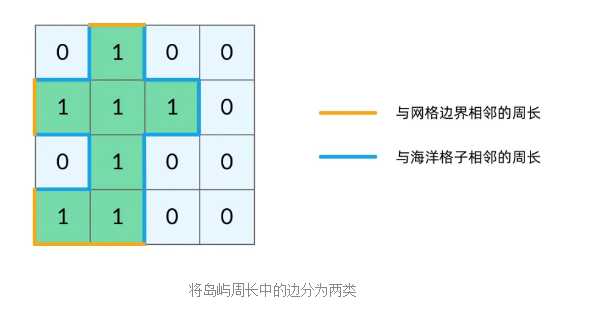
那么这些和我们岛屿的周长有什么关系呢？实际上，岛屿的周长是计算岛屿全部的「边缘」，而这些边缘就是我们在 DFS 遍历中，dfs 函数返回的位置。观察题目示例，我们可以将岛屿的周长中的边分为两类，如下图所示。黄色的边是与网格边界相邻的周长，而蓝色的边是与海洋格子相邻的周长。

 

 当我们的 dfs 函数因为「坐标 (r, c) 超出网格范围」返回的时候，实际上就经过了一条黄色的边；而当函数因为「当前格子是海洋格子」返回的时候，实际上就经过了一条蓝色的边。这样，我们就把岛屿的周长跟 DFS 遍历联系起来了，我们的题解代码也呼之欲出：

 

 1 public int islandPerimeter(int[][] grid) {
 2     for (int r = 0; r < grid.length; r++) {
 3         for (int c = 0; c < grid[0].length; c++) {
 4             if (grid[r][c] == 1) {
 5                 // 题目限制只有一个岛屿，计算一个即可
 6                 return dfs(grid, r, c);
 7             }
 8         }
 9     }
10     return 0;
11 }
12 
13 int dfs(int[][] grid, int r, int c) {
14     // 函数因为「坐标 (r, c) 超出网格范围」返回，对应一条黄色的边
15     if (!inArea(grid, r, c)) {
16         return 1;
17     }
18     // 函数因为「当前格子是海洋格子」返回，对应一条蓝色的边
19     if (grid[r][c] == 0) {
20         return 1;
21     }
22     // 函数因为「当前格子是已遍历的陆地格子」返回，和周长没关系
23     if (grid[r][c] != 1) {
24         return 0;
25     }
26     grid[r][c] = 2;
27     return dfs(grid, r - 1, c)
28         + dfs(grid, r + 1, c)
29         + dfs(grid, r, c - 1)
30         + dfs(grid, r, c + 1);
31 }
32 
33 // 判断坐标 (r, c) 是否在网格中
34 boolean inArea(int[][] grid, int r, int c) {
35     return 0 <= r && r < grid.length 
36          && 0 <= c && c < grid[0].length;
37 }

文章出处：https://mp.weixin.qq.com/s?__biz=MzA5ODk3ODA4OQ==&mid=2648167208&idx=1&sn=d8118c7c0e0f57ea2bdd8aa4d6ac7ab7&chksm=88aa236ebfddaa78a6183cf6dcf88f82c5ff5efb7f5c55d6844d9104b307862869eb9032bd1f&token=1064083695&lang=zh_CN#rd