强连通分量

Posted 2020-12-15 zjnu-huyh

今天听了ztcdl的讲解，队友lkt，cyx带了我几道模板题，突然感觉自己行了（可能自己还没睡醒，才有勇气写板子了）

---

强连通分量的预备姿势：

①树上的DFS序（时间戳）：一句话，就是按照dfs的遍历顺序，把每个点再对应一个dfn数组，dfn[i]存的就是dfs序的时间戳。

②DFS树：就是在DFS时通向还没有访问过的点的那些边所形成的树。不在树上的边统称为非树边，对于无向图，就只有返祖边；对于有向图，有返祖边、横叉边、前向边。

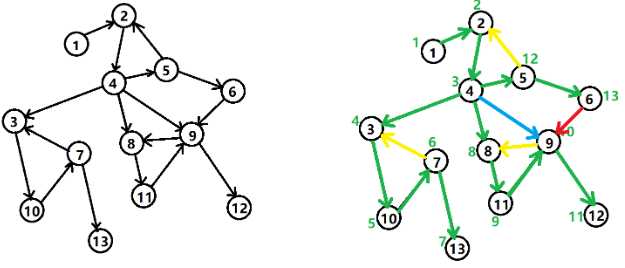
黄色的为：返祖边（指向其祖先）

蓝色的为：前向边（跨过儿子指孙子）

红色的为：横叉边（指向别的子树）

③强联通的概念

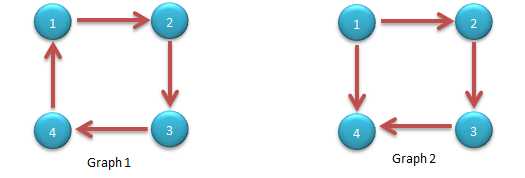
例如：

  图一：所有点都可以走到这个强联通分量中的任意一个点（属于强联通SCC）

  图二：显然不满足SCC

④缩点的思想

在找到强联通之后，我们可以将一个强连通分量视为一个点，从而构造DAG。

---

SCC的代码理解：

我们发现，横叉边会影响判断，所以应该直接删去；前向边不影响答案，可以无视它；只有返祖边才会形成SCC。

const int maxn = 1e4 + 10;
vector<int>Map[maxn];
vector<int>a[maxn];
int n, m;
int low[maxn];      //low[i]表示从i出发能够回到的最远的祖先
int sccno[maxn];    //sccno[i]表示i属于第sccno[i]个强连通分量
int dfn[maxn];      //DFS序就是DFS时某个点是第几个被访问的,用dfn[i]表示i的时间戳，
int dfs_clock;      //时间戳
int scc_cnt;        //强连通分量的个数
stack<int>S;
int num[maxn];      //num[i]表示第i个强连通分量中存在多少点
void tarjan(int u)  //dfs(u)结束后 low[u]、pre[u]将会求出
{
    dfn[u] = low[u] = ++dfs_clock;
    S.push(u);
    for (int i = 0; i < Map[u].size(); i++)//u->v
    {
        int v = Map[u][i];
        if (!dfn[v])               //说明v还未被dfs
        {
            tarjan(v);             //会自动求出low[v]、dfn[v]
            low[u] = min(low[u], low[v]);
        }
        else if (!sccno[v])        //说明v正在dfs：只求出了dfn[v]
            low[u] = min(low[u], dfn[v]);
    }
    if (dfn[u] == low[u])          //说明找到了一个强连通分量
    {
        scc_cnt++;
        for (;;)
        {
            int x = S.top(); S.pop();
            sccno[x] = scc_cnt;
            num[scc_cnt]++;
            a[scc_cnt].push_back(x);
            if (x == u)break;
        }
    }
}

void find_scc()
{
    dfs_clock = scc_cnt = 0;
    memset(dfn, 0, sizeof(dfn));
    memset(low, 0, sizeof(low));
    memset(sccno, 0, sizeof(sccno));
    for (int i = 1; i <= n; i++)
        if (!dfn[i])              //dfn[i] == 0 说明还没走第i个点
            tarjan(i);
}

可以手模一下下图：

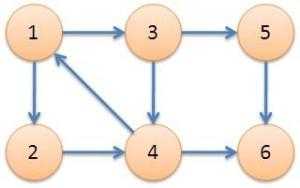
先应该将边3->4，5->6直接删去

之后,初始化栈为empty

①1进入，dfn[1]=low[1]=++cnt=1   栈:1

②1->2 dfn[2]=low[2]=++cnt=2    栈: 1 2

③2->4 dfn[4]=low[4]=++cnt=3    栈: 1 2 4

④4->6 dfn[6]=low[6]=++cnt=4    栈: 1 2 4 6

6无出度，dfn[6]==low[6]，说明6是SCC的根节点

回溯到4后发现4找到了一个已经在栈中的点1，更新low[4]，于是 low[4]=1

由4继续回到2 low[2]=1；

由2继续回到1 low[1]=1；

另一支，low[5]=dfn[5]=6；

由5继续回到3 low[3]=5；

由3继续回到1 low[1]=1；

画图更快：（橙色为dfn，蓝色为low）

---

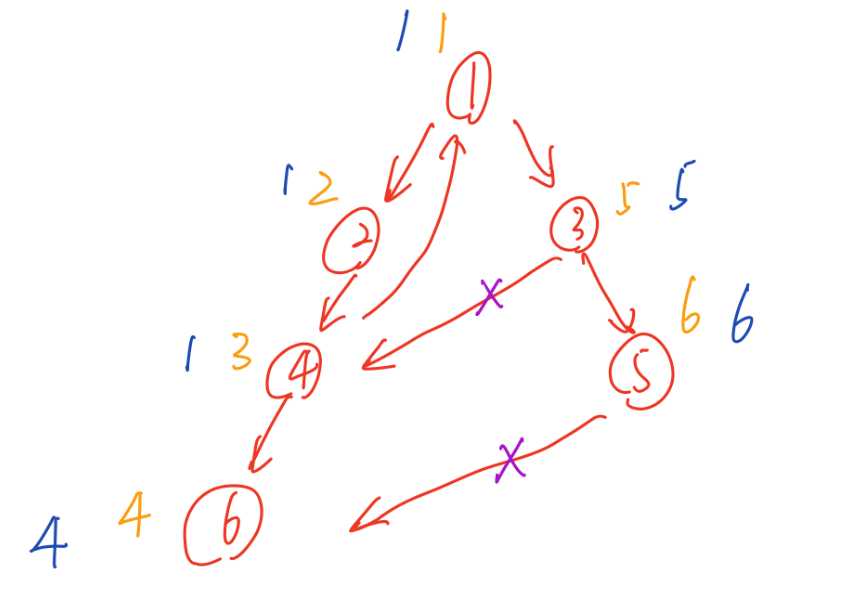
例题：POJ1236 Network of Schools

题面：

题意：输入N行，第i行就表示，i与第i行中的所有数字x有一条i->x的边，每行以0结尾，第一行输出至少发几次能让所有学校收到软件；第二行输出如果只发一次，还需要添加几条线路。

题解：裸题，题A直接跑tarjan即可，缩点后，需要向所有入度为0的点发送信息

题B，统计一下缩完点后入度为0，出度为0的点的个数，贪心策略——入度为0的点和出度为0的点相连，答案为：max（入度0，出度0）

需要注意，特判天然是一个SCC的情况(此情况题B无需加边，如果不特判会被看成max(出度0，入度0)=1)。

#include <iostream> 
#include <stack>
#include <vector>
#include <algorithm>
#include <cstring>
using namespace std;
typedef long long ll;
const int maxn = 1e4 + 10;
vector<int>Map[maxn];
vector<int>a[maxn];
int n, m;
int low[maxn];      //low[i]表示从i出发能够回到的最远的祖先
int sccno[maxn];    //sccno[i]表示i属于第sccno[i]个强连通分量
int dfn[maxn];      //DFS序就是DFS时某个点是第几个被访问的,用dfn[i]表示i的时间戳，
int dfs_clock;      //时间戳
int scc_cnt;        //强连通分量的个数

stack<int>S;
int num[maxn];      //num[i]表示第i个强连通分量中存在多少点
void tarjan(int u)  //dfs(u)结束后 low[u]、pre[u]将会求出
{
    dfn[u] = low[u] = ++dfs_clock;
    S.push(u);
    for (int i = 0; i < Map[u].size(); i++)//u->v
    {
        int v = Map[u][i];
        if (!dfn[v])               //说明v还未被dfs
        {
            tarjan(v);             //会自动求出low[v]、dfn[v]
            low[u] = min(low[u], low[v]);
        }
        else if (!sccno[v])        //说明v正在dfs：只求出了dfn[v]
            low[u] = min(low[u], dfn[v]);
    }
    if (dfn[u] == low[u])          //说明找到了一个强连通分量
    {
        scc_cnt++;
        for (;;)
        {
            int x = S.top(); S.pop();
            sccno[x] = scc_cnt;
            num[scc_cnt]++;
            a[scc_cnt].push_back(x);
            if (x == u)break;
        }
    }
}
void find_scc()
{
    dfs_clock = scc_cnt = 0;
    memset(dfn, 0, sizeof(dfn));
    memset(low, 0, sizeof(low));
    memset(sccno, 0, sizeof(sccno));
    for (int i = 1; i <= n; i++)
        if (!dfn[i])              //dfn[i] == 0 说明还没走第i个点
            tarjan(i);
}
int in[maxn];//记录重构图后的入度
int out[maxn];//记录重构图后的出度
void init(void)
{
    memset(num, 0, sizeof(num));
    memset(in, 0, sizeof(in));
    memset(out, 0, sizeof(out));
    for (int i = 0; i < maxn; i++)
        Map[i].clear(), a[i].clear();
}
int main()
{
    cin >> n;
    init();
    for (int i = 1; i <= n; i++)
    {
        int k;
        while (cin >> k)
        {
            if (k == 0)break;
            Map[i].push_back(k);
        }
    }
    find_scc();//找出所有的强连通分量
    //缩点
    for (int u = 1; u <= n; u++)
    {
        for (int i = 0; i < Map[u].size(); ++i)//for(int i=0;i<Map[u].size();++i){v=Map[u][i]}
        {
            int v = Map[u][i];
            if (sccno[u] == sccno[v])
                continue;
            in[sccno[v]]++;
            out[sccno[u]]++;
        }
    }
    if (scc_cnt == 1)
        cout << 1 << endl << 0 << endl;
    else 
    {
        ll ans = 0;
        int in_n = 0, out_n = 0;
        for (int i = 1; i <= scc_cnt; i++)
        {
            if (in[i] == 0)
                in_n++;
            if (out[i] == 0)
                out_n++;
        }
        cout << in_n <<endl;
        cout << max(in_n, out_n) << endl;
    }
    return 0;
}

---

例题：HDU1269 迷宫城堡

题面：

题意：找是否存在一个SCC满足包含所有点

题解：裸题，直接跑tarjan即可，法①判断是否只有一个SCC；法②判断是否存在n个点的SCC

代码：

#include <iostream> 
#include <stack>
#include <vector>
#include <algorithm>
#include <cstring>
using namespace std;
const int maxn = 1e4 + 10;
vector<int>Map[maxn];
vector<int>a[maxn];
int n, m;
int low[maxn];       //low[i]表示从i出发能够回到的最远的祖先
int sccno[maxn];     //sccno[i]表示i属于第sccno[i]个强连通分量
int dfn[maxn];       //DFS序就是DFS时某个点是第几个被访问的,用dfn[i]表示i的时间戳，
int dfs_clock;       //时间戳
int scc_cnt;         //强连通分量的个数
                    
stack<int>S;
int num[maxn];//num[i]表示第i个强连通分量中存在多少点
void tarjan(int u)//dfs(u)结束后 low[u]、pre[u]将会求出
{
    dfn[u] = low[u] = ++dfs_clock;
    S.push(u);
    for (auto v : Map[u])//u->v
    {
        if (!dfn[v])//说明v还未被dfs
        {
            tarjan(v);//会自动求出low[v]、dfn[v]
            low[u] = min(low[u], low[v]);
        }
        else if (!sccno[v])//说明v正在dfs：只求出了dfn[v]
            low[u] = min(low[u], dfn[v]);
    }
    if (dfn[u] == low[u])//说明找到了一个强连通分量
    {
        scc_cnt++;
        for (;;)
        {
            int x = S.top(); S.pop();
            sccno[x] = scc_cnt;
            num[scc_cnt]++;
            a[scc_cnt].push_back(x);
            if (x == u)break;
        }
    }
}
void find_scc()
{
    dfs_clock = scc_cnt = 0;
    memset(dfn, 0, sizeof(dfn));
    memset(low, 0, sizeof(low));
    memset(sccno, 0, sizeof(sccno));
    for (int i = 1; i <= n; i++)
        if (!dfn[i])//dfn[i] == 0 说明还没走第i个点
            tarjan(i);
}
int main()
{
    while (cin >> n >> m)
    {
        if (n == 0 && m == 0)break;
        memset(num, 0, sizeof(num));
        for (int i = 0; i < maxn; i++)
            Map[i].clear(), a[i].clear();
        for (int i = 1; i <= m; i++)
        {
            int u, v;
            cin >> u >> v;
            Map[u].push_back(v);
        }
        find_scc();//找出所有的强连通分量
        int flag = 0;
        for (int i = 1; i <= scc_cnt; i++)
        {
            if (num[i] == n)
                flag = 1;
        }
        if (flag == 1)
            cout << "Yes" << endl;
        else
            cout << "No" << endl;
    }
    return 0;
}

例题：P2341 [USACO03FALL][HAOI2006]受欢迎的牛 G

题面：

题意：缩点后找出度为0的点是否唯一，如果唯一，则认为是这个点的整体是受欢迎的，直接输出这个（可能缩过的）点包含的总点数。

如果在缩点后有多个出度为0的点，显然不是在一条链上，一定不符合题意。

代码：

#include <iostream> 
#include <stack>
#include <vector>
#include <algorithm>
#include <cstring>
using namespace std;
const int maxn = 1e4 + 10;
vector<int>Map[maxn];
int n, m;
int low[maxn];   //low[i]表示从i出发能够回到的最远的祖先
int sccno[maxn]; //sccno[i]表示i属于第sccno[i]个强连通分量
int dfn[maxn];   //DFS序就是DFS时某个点是第几个被访问的,用dfn[i]表示i的时间戳
int dfs_clock;   //时间戳
int scc_cnt;     //强连通分量的个数

stack<int>S;
int num[maxn];//num[i]表示第i个强连通分量中存在多少点
vector<int>a[maxn];
void tarjan(int u)//dfs(u)结束后 low[u]、pre[u]将会求出
{
    dfn[u] = low[u] = ++dfs_clock;
    S.push(u);
    for (auto v : Map[u])//u->v
    {
        if (!dfn[v])//说明v还未被dfs
        {
            tarjan(v);//会自动求出low[v]、dfn[v]
            low[u] = min(low[u], low[v]);
        }
        else if (!sccno[v])//说明v正在dfs：只求出了dfn[v]
            low[u] = min(low[u], dfn[v]);
    }
    if (dfn[u] == low[u])//说明找到了一个强连通分量
    {
        scc_cnt++;
        for (;;)
        {
            int x = S.top(); S.pop();
            sccno[x] = scc_cnt;
            num[scc_cnt]++;
            a[scc_cnt].push_back(x);
            if (x == u)break;
        }
    }
}

void find_scc()
{
    dfs_clock = scc_cnt = 0;
    memset(dfn, 0, sizeof(dfn));
    memset(sccno, 0, sizeof(sccno));
    for (int i = 1; i <= n; i++)
        if (!dfn[i])//dfn[i] == 0 说明还没走第i个点
            tarjan(i);
}

int chu[maxn];//chu[i]表示第i个强连通分量的出度
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= m; i++)
    {
        int u, v;
        cin >> u >> v;
        Map[u].push_back(v);
    }
    find_scc();//找出所有的强连通分量
    for (int u = 1; u <= n; u++)//重建图
    {
        for (auto v : Map[u])
        {
            //u->v
            if (sccno[u] == sccno[v])//说明u,v属于同一个
                continue;
            chu[sccno[u]]++;
        }
    }
    //缩点后 scc_cnt个点
    int number = 0, ans;//number表示出度为0的强连通分量的数量
    for (int i = 1; i <= scc_cnt; i++)
        if (chu[i] == 0)//出度为0
        {
            number++;
            ans = num[i];
        }
    if (number != 1)ans = 0;
    cout << ans << endl;
    return 0;
}

---

例题：HDU5934 Bomb 

题面：

题解：先根据题意构图，题意为A、B中心点的距离如果小于A的爆炸半径，认为A->B有一条有向边；如果小于B的爆炸半径，则认为B->A有一条有向边

所以只要先存图，存完之后就是一个tarjan的裸题。

代码：

#include <iostream> 
#include <stack>
#include <vector>
#include <algorithm>
#include <cstring>
using namespace std;
typedef long long ll;
const int maxn = 1e4 + 10;
vector<int>Map[maxn];
vector<int>a[maxn];
int n, m;
int low[maxn];      //low[i]表示从i出发能够回到的最远的祖先
int sccno[maxn];    //sccno[i]表示i属于第sccno[i]个强连通分量
int dfn[maxn];      //DFS序就是DFS时某个点是第几个被访问的,用dfn[i]表示i的时间戳
int dfs_clock;      //时间戳
int scc_cnt;        //强连通分量的个数

stack<int>S;
int num[maxn];//num[i]表示第i个强连通分量中存在多少点
void tarjan(int u)//dfs(u)结束后 low[u]、pre[u]将会求出
{
    dfn[u] = low[u] = ++dfs_clock;
    S.push(u);
    for (auto v : Map[u])//u->v
    {
        if (!dfn[v])//说明v还未被dfs
        {
            tarjan(v);//会自动求出low[v]、dfn[v]
            low[u] = min(low[u], low[v]);
        }
        else if (!sccno[v])//说明v正在dfs：只求出了dfn[v]
            low[u] = min(low[u], dfn[v]);
    }
    if (dfn[u] == low[u])//说明找到了一个强连通分量
    {
        scc_cnt++;
        for (;;)
        {
            int x = S.top(); S.pop();
            sccno[x] = scc_cnt;
            num[scc_cnt]++;
            a[scc_cnt].push_back(x);
            if (x == u)break;
        }
    }
}
void find_scc()
{
    dfs_clock = scc_cnt = 0;
    memset(dfn, 0, sizeof(dfn));
    memset(low, 0, sizeof(low));
    memset(sccno, 0, sizeof(sccno));
    for (int i = 1; i <= n; i++)
        if (!dfn[i])//dfn[i] == 0 说明还没走第i个点
            tarjan(i);
}
struct node {
    ll x, y, r, c;
}p[maxn];
ll col(ll x1, ll y1, ll x2, ll y2)
{
    ll dis = (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2);
    return dis;
}
ll cost_min[maxn];//记录第i个强连通分量的最小费用
int in[maxn];//记录重构图后的入度
void init(void)
{
    memset(num, 0, sizeof(num));
    memset(cost_min, 0x3f, sizeof(cost_min));
    memset(in, 0, sizeof(in));
    for (int i = 0; i < maxn; i++)
        Map[i].clear(), a[i].clear();
}
int main()
{
    int t; cin >> t;
    for (int num = 1; num <= t; num++)
    {
        init();
        cin >> n;
        for (int i = 1; i <= n; i++)
            cin >> p[i].x >> p[i].y >> p[i].r >> p[i].c;
        for (int i = 1; i <= n; i++)
        {
            for (int j = i + 1; j <= n; j++)
            {
                if (col(p[i].x, p[i].y, p[j].x, p[j].y) <= p[i].r * p[i].r)
                    Map[i].push_back(j);
                if (col(p[i].x, p[i].y, p[j].x, p[j].y) <= p[j].r * p[j].r)
                    Map[j].push_back(i);
            }
        }
        find_scc();//找出所有的强连通分量
        for (int i = 1; i <= n; i++)
            cost_min[sccno[i]] = min(cost_min[sccno[i]], p[i].c);
        //缩点
        for (int u = 1; u <= n; u++)
        {
            for (auto v : Map[u])
            {
                if (sccno[u] == sccno[v])
                    continue;
                in[sccno[v]]++;
            }
        }
        ll ans = 0;
        for (int i = 1; i <= scc_cnt; i++)
        {
            if (in[i] == 0)
                ans += cost_min[i];
        }
        printf("Case #%d: %lld
", num, ans);
    }
    return 0;
}